Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нахождение ранга матрицы методом окаймляющих миноров.Содержание книги
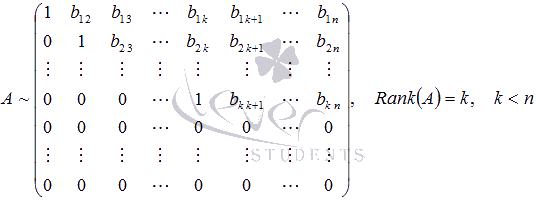
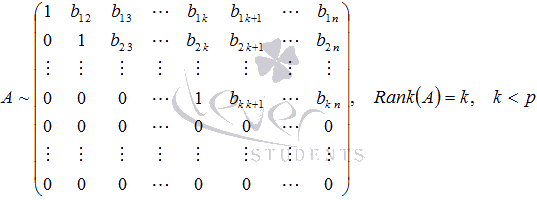
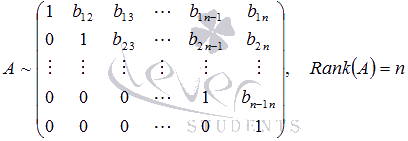
Поиск на нашем сайте Существуют другие методы нахождения ранга матрицы, которые позволяют получить результат при меньшей вычислительной работе. Одним из таких методов является метод окаймляющих миноров. Разберемся с понятием окаймляющего минора. Говорят, что минор Мок (k+1)-ого порядка матрицы А окаймляет минор M порядка k матрицы А, если матрица, соответствующая минору Мок, «содержит» матрицу, соответствующую минору M. Другими словами, матрица, соответствующая окаймляемому минору М, получается из матрицы, соответствующей окаймляющему минору Mок, вычеркиванием элементов одной строки и одного столбца. Для примера рассмотрим матрицу Метод окаймляющих миноров обосновывается следующей теоремой (приведем ее формулировку без доказательства). Теорема. Если все миноры, окаймляющие минор k-ого порядка матрицы А порядка p на n, равны нулю, то все миноры порядка (k+1) матрицы А равны нулю. Таким образом, для нахождения ранга матрицы не обязательно перебирать все миноры, достаточно окаймляющих. Количество миноров, окаймляющих минор k -ого порядка матрицы А порядка Перейдем к нахождению ранга матрицы методом окаймляющих миноров. Кратко опишем алгоритм этого метода. Если матрица А ненулевая, то в качестве минора первого порядка берем любой элемент матрицы А, отличный от нуля. Рассматриваем его окаймляющие миноры. Если все они равны нулю, то ранг матрицы равен единице. Если же есть хотя бы один ненулевой окаймляющий минор (его порядок равен двум), то переходим к рассмотрению его окаймляющих миноров. Если все они равны нулю, то Rank(A) = 2. Если хотя бы один окаймляющий минор отличен от нуля (его порядок равен трем), то рассматриваем его окаймляющие миноры. И так далее. В итоге Rank(A) = k, если все окаймляющие миноры (k + 1)-ого порядка матрицы А равны нулю, либо Rank(A) = min(p, n), если существует ненулевой минор, окаймляющий минор порядка (min(p, n) – 1). Разберем метод окаймляющих миноров для нахождения ранга матрицы на примере. Пример. Найдите ранг матрицы Решение. Так как элемент a1 1 матрицы А отличен от нуля, то возьмем его в качестве минора первого порядка. Начнем поиск окаймляющего минора, отличного от нуля: Найден окаймляющий минор второго порядка, отличный от нуля Все миноры, окаймляющие минор второго порядка Ответ: Rank(A) = 2. Пример. Найдите ранг матрицы Решение. В качестве отличного от нуля минора первого порядка возьмем элемент a1 1 = 1 матрицы А. Окаймляющий его минор второго порядка Ответ: Rank(A) = 3. К началу страницы Нахождение ранга с помощью элементарных преобразований матрицы (методом Гаусса). Рассмотрим еще один способ нахождения ранга матрицы. Следующие преобразования матрицы называют элементарными: · перестановка местами строк (или столбцов) матрицы; · умножение всех элементов какой-либо строки (столбца) матрицы на произвольное число k, отличное от нуля; · прибавление к элементам какой-либо строки (столбца) соответствующих элементов другой строки (столбца) матрицы, умноженных на произвольное число k. Матрица В называется эквивалентной матрице А, если В получена из А с помощью конечного числа элементарных преобразований. Эквивалентность матриц обозначается символом «~», то есть, записывается A ~ B. Нахождение ранга матрицы с помощью элементарных преобразований матрицы основано на утверждении: если матрица В получена из матрицы А с помощью конечного числа элементарных преобразований, то Rank(A) = Rank(B). Справедливость этого утверждения следует из свойств определителя матрицы: · При перестановке строк (или столбцов) матрицы ее определитель меняет знак. Если он равен нулю, то при перестановке строк (столбцов) он остается равным нулю. · При умножении всех элементов какой-либо строки (столбца) матрицы на произвольное число k отличное от нуля, определитель полученной матрицы равен определителю исходной матрицы, умноженному на k. Если определитель исходной матрицы равен нулю, то после умножения всех элементов какой-либо строки или столбца на число k определитель полученной матрицы также будет равен нулю. · Прибавление к элементам некоторой строки (столбца) матрицы соответствующих элементов другой строки (столбца) матрицы, умноженных на некоторое число k, не изменяет ее определителя. Суть метода элементарных преобразований заключается в приведении матрицы, ранг которой нам требуется найти, к трапециевидной (в частном случае к верхней треугольной) с помощью элементарных преобразований. Для чего это делается? Ранг матриц такого вида очень легко найти. Он равен количеству строк, содержащих хотя бы один ненулевой элемент. А так как ранг матрицы при проведении элементарных преобразований не изменяется, то полученное значение будет рангом исходной матрицы. Приведем иллюстрации матриц, одна из которых должна получиться после преобразований. Их вид зависит от порядка матрицы. · Для прямоугольных матриц А порядка p на n, число строк которых больше числа столбцов (p > n). · Для прямоугольных матриц А порядка p на n, число строк которых меньше числа столбцов (p < n). · Для квадратных матриц А порядка n на n. Эти иллюстрации являются шаблонами, к которым будем преобразовывать матрицу А. Опишем алгоритм метода. Пусть нам требуется найти ранг ненулевой матрицы А порядка Будем считать, что элемент a11 отличен от нуля. В противном случае мы можем перестановкой строк и (или) столбцов преобразовать матрицу так, чтобы «новый» элемент a11 стал ненулевым. Итак, К элементам второй строки полученной матрицы А(1) прибавим соответствующие элементы первой строки, умноженные на Если все элементы полученной матрицы, находящиеся в строках со второй по p-ую, равны нулю, то ранг этой матрицы равен единице, а, следовательно, и ранг исходной матрицы равен единице. Если же в строках со второй по p-ую есть хотя бы один ненулевой элемент, то продолжаем проводить преобразования. Причем действуем абсолютно аналогично, но лишь с отмеченной на рисунке частью матрицы А(2) Если Итак, К элементам третьей строки полученной матрицы А(3) прибавим соответствующие элементы второй строки, умноженные на Если все элементы полученной матрицы, находящиеся в строках с третьей по p-ую, равны нулю, то ранг этой матрицы равен двум, а, следовательно, Rank(A) = 2. Если же в строках с третьей по p-ую есть хотя бы один ненулевой элемент, то продолжаем проводить преобразования. Причем действуем абсолютно аналогично, но лишь с отмеченной на рисунке частью матрицы А(4): И так действуем дальше, пока не придем к одному из рассмотренных выше шаблонов, что позволит определить ранг исходной матрицы. Разберем решения нескольких примеров. Пример. Найдите ранг матрицы Решение. Так как элемент a1 1 отличен от нуля, то умножим элементы первой строки матрицы А на Прибавим к элементам второй строки соответствующие элементы первой строки, умноженные на (- 3). К элементам третьей строки прибавим элементы первой строки, умноженные на (- 1). И так далее: Элемент К элементам третьей строки полученной матрицы прибавляем соответствующие элементы второй строки, умноженные на Все элементы третьей, четвертой и пятой строк полученной матрицы равны нулю. Так с помощью элементарных преобразований мы привели матрицу А к трапецеидальному виду, откуда видно, что Rank(A(4)) = 2. Следовательно, ранг исходной матрицы также равен двум. Замечание. ОБРАТИТЕ ВНИМАНИЕ: при проведении элементарных преобразований не допускаются приближенные вычисления! Рассмотрим еще один пример. Пример. Методом элементарных преобразований найдите ранг матрицы Решение. Поменяем местами первую и вторую строки матрицы А, так как элемент a1 1 равен нулю, а элемент a21 отличен от нуля: В полученной матрице элемент Так первый столбец преобразован к нужному виду. Элемент Второй столбец полученной матрицы имеет нужный вид, так как элемент Так как Умножим третью строку полученной матрицы на На этом заканчиваем преобразования. Получаем Rank(A(5))=3, следовательно, Rank(A)=3. Ответ: ранг исходной матрицы равен трем. 9. Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:
Пояснения Система уравнений Доказательство (условия совместности системы)[править | править вики-текст] Необходимость Пусть система совместна. Тогда существуют числа Достаточность Пусть Следствия · Количество главных переменных системы равно рангу системы. · Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных. · Система линейных уравнений является однородной, если свободный член каждого уравнения системы равен нулю. Например: · Совершенно ясно, что однородная система всегда совместна, то есть всегда имеет решение. И, прежде всего, в глаза бросается так называемое тривиальное решение · Пример 1 · Решить однородную систему линейных уравнений · Решение: чтобы решить однородную систему необходимо записать матрицу системы и с помощью элементарных преобразований привести её к ступенчатому виду. Обратите внимание, что здесь отпадает необходимость записывать вертикальную черту и нулевой столбец свободных членов – ведь что ни делай с нулями, они так и останутся нулями: · (1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –3. · (2) К третьей строке прибавили вторую строку, умноженную на –1. · Делить третью строку на 3 не имеет особого смысла. · В результате элементарных преобразований получена эквивалентная однородная система · Ответ: · Сформулируем очевидный критерий: однородная система линейных уравнений имеет только тривиальное решение, если ранг матрицы системы (в данном случае 3) равен количеству переменных (в данном случае · Разогреваемся и настраиваем свой радиоприёмник на волну элементарных преобразований: · Пример 2 · Решить однородную систему линейных уравнений · Из статьи Как найти ранг матрицы? вспоминаем рациональный приём попутного уменьшения чисел матрицы. В противном случае вам придётся разделывать крупную, а частенько и кусачую рыбу. Примерный образец оформления задания в конце урока. · Нули – это хорошо и удобно, однако на практике гораздо более распространен случай, когда строки матрицы системы линейно зависимы. И тогда неизбежно появление общего решения: · Пример 3 · Решить однородную систему линейных уравнений · Решение: запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду. Первое действие направлено не только на получение единичного значения, но и на уменьшение чисел в первом столбце: · (1) К первой строке прибавили третью строку, умноженную на –1. Ко второй строке прибавили третью строку, умноженную на –2. Слева вверху я получил единицу с «минусом», что зачастую намного удобнее для дальнейших преобразований. · (2) Первые две строки одинаковы, одну из них удалили. Честное слово, не подгонял решение – так получилось. Если выполнять преобразования шаблонно, то линейная зависимость строк обнаружилась бы чуть позже. · (3) К третьей строке прибавили вторую строку, умноженную на 3. · (4) У первой строки сменили знак. · В результате элементарных преобразований получена эквивалентная система: · Алгоритм работает точно так же, как и для неоднородных систем. Переменные · Выразим базисные переменные через свободную переменную: · Ответ: общее решение: · Тривиальное решение входит в общую формулу, и записывать его отдельно излишне. · Проверка выполняется тоже по обычной схеме: полученное общее решение необходимо подставить в левую часть каждого уравнения системы и получить законный ноль при всех подстановках. · На этом можно было бы тихо-мирно закончить, но решение однородной системы уравнений часто требуется представить в векторной форме с помощью фундаментальной системы решений. Пожалуйста, временно забудьте об аналитической геометрии, поскольку сейчас речь пойдёт о векторах в алгебраическом смысле, который я немного приоткрыл в статье про ранг матрицы и окончательно расписал на уроке о линейных преобразованиях. Терминологии тушеваться не нужно, всё довольно просто: · Фундаментальная система решений однородной системы уравнений · Фундаментальная система решений – это множество линейно независимых векторов · Количество векторов · Однако в практических заданиях гораздо удобнее ориентироваться на следующий признак: количество векторов · Представим общее решение Примера №3 · Координаты вектора · Ответ следует записать в виде линейной комбинации векторов фундаментальной системы. В нашей ситуации линейная комбинация состоит из одинокого слагаемого. Общее решение однородной системы я буду обозначать через вектор · Ответ: общее решение: · Придавая параметру · Это мы рассмотрели традиционный способ построения фундаментальной системы в так называемом нормальном виде – когда свободным переменным придаются исключительно единичные значения. Но правила хорошего математического тона предписывают избавляться от дробей, если это возможно. Поэтому в данном случае можно взять · И тогда ответ запишется в эквивалентной форме: Линейное многообразие Линейным многообразием в линейном пространстве
для каких-то фиксированных подпространства
Если В частности, Если Пересечение линейных многообразий всегда является линейным многообразием. Размерность линейного многообразия
|
|||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1704; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.009 с.) |

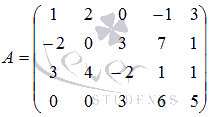 и возьмем минор второго порядка
и возьмем минор второго порядка 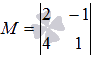 . Запишем все окаймляющие миноры:
. Запишем все окаймляющие миноры:
 , находится по формуле
, находится по формуле 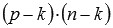 . Отметим, что миноров, окаймляющих минор k-ого порядка матрицы А, не больше, чем миноров (k + 1)-ого порядка матрицы А. Поэтому, в большинстве случаев использование метода окаймляющих миноров выгоднее простого перебора всех миноров.
. Отметим, что миноров, окаймляющих минор k-ого порядка матрицы А, не больше, чем миноров (k + 1)-ого порядка матрицы А. Поэтому, в большинстве случаев использование метода окаймляющих миноров выгоднее простого перебора всех миноров.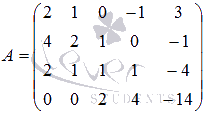 методом окаймляющих миноров.
методом окаймляющих миноров.
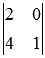 . Переберем его окаймляющие миноры (их
. Переберем его окаймляющие миноры (их 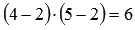 штук):
штук):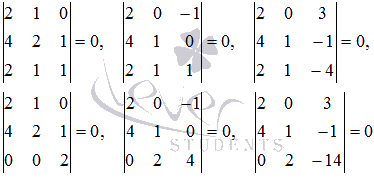
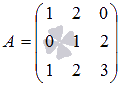 с помощью окаймляющих миноров.
с помощью окаймляющих миноров.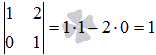 не равен нулю. Этот минор окаймляется минором третьего порядка
не равен нулю. Этот минор окаймляется минором третьего порядка 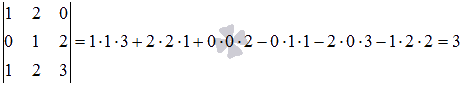 . Так как он не равен нулю и для него не существует ни одного окаймляющего минора, то ранг матрицы А равен трем.
. Так как он не равен нулю и для него не существует ни одного окаймляющего минора, то ранг матрицы А равен трем.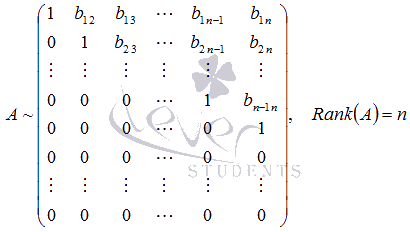
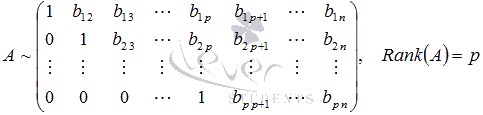
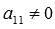 . Умножим все элементы первой строки матрицы А на
. Умножим все элементы первой строки матрицы А на 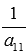 . При этом получим эквивалентную матрицу, обозначим ее А(1):
. При этом получим эквивалентную матрицу, обозначим ее А(1):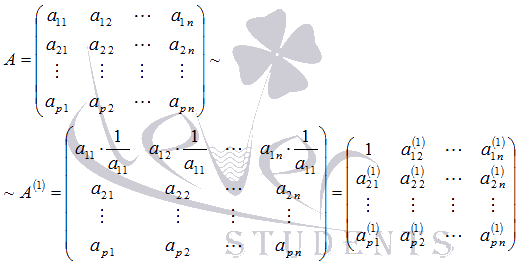
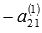 . К элементам третьей строки прибавим соответствующие элементы первой строки, умноженные на
. К элементам третьей строки прибавим соответствующие элементы первой строки, умноженные на 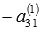 . И так далее до p-ой строки. Получим эквивалентную матрицу, обозначим ее А(2):
. И так далее до p-ой строки. Получим эквивалентную матрицу, обозначим ее А(2):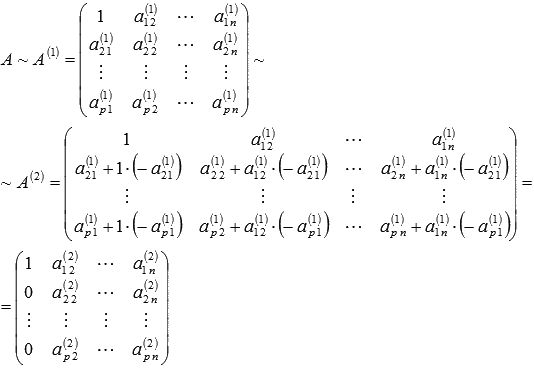
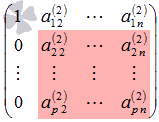
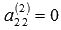 , то переставляем строки и (или) столбцы матрицы А(2) так, чтобы «новый» элемент
, то переставляем строки и (или) столбцы матрицы А(2) так, чтобы «новый» элемент  стал ненулевым.
стал ненулевым.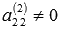 . Умножаем каждый элемент второй строки матрицы А(2) на
. Умножаем каждый элемент второй строки матрицы А(2) на 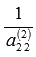 . Получаем эквивалентную матрицу А(3):
. Получаем эквивалентную матрицу А(3):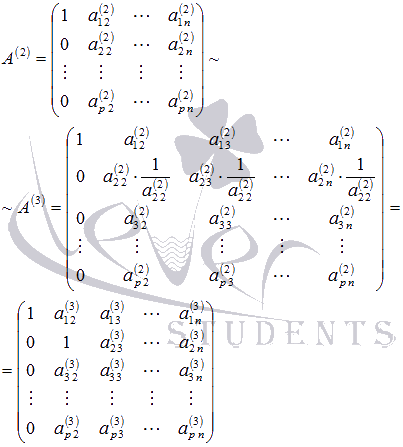
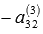 . К элементам четвертой строки прибавим соответствующие элементы второй строки, умноженные на
. К элементам четвертой строки прибавим соответствующие элементы второй строки, умноженные на 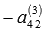 . И так далее до p-ой строки. Получим эквивалентную матрицу, обозначим ее А(4):
. И так далее до p-ой строки. Получим эквивалентную матрицу, обозначим ее А(4):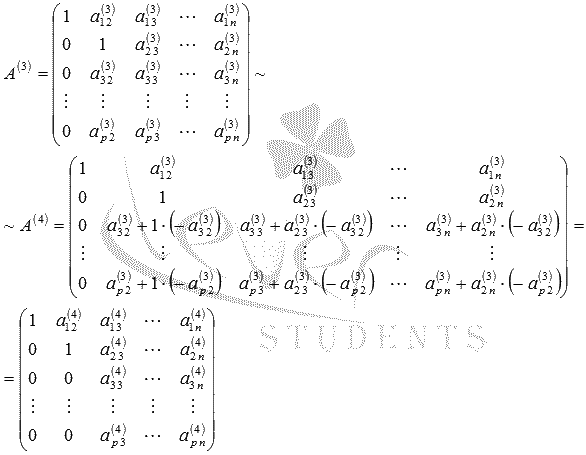
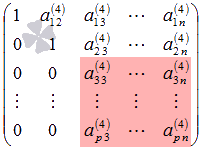
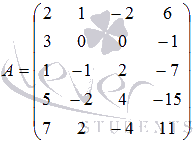 с помощью элементарных преобразований.
с помощью элементарных преобразований.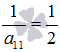 :
: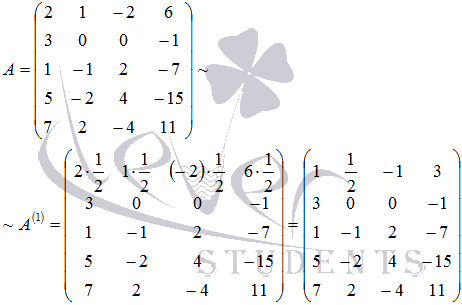
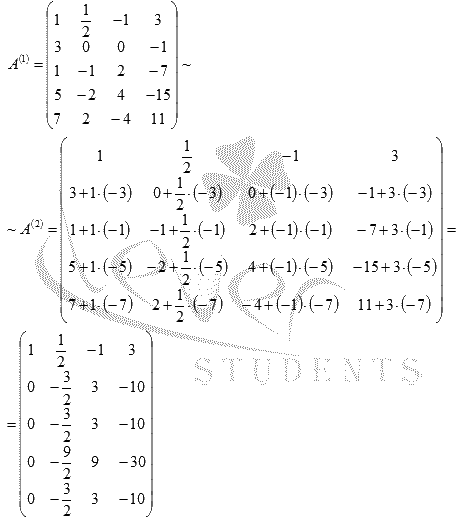
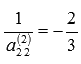 :
: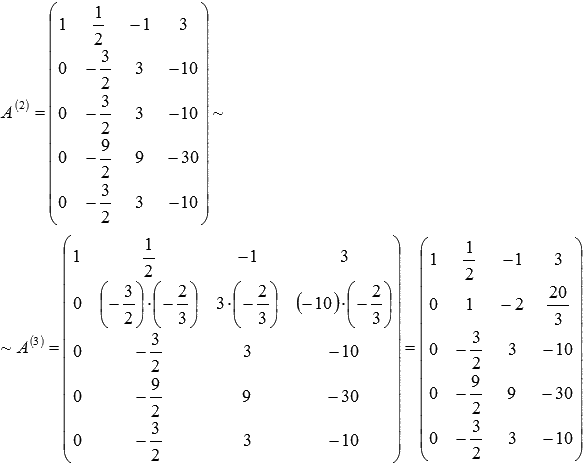
 ; к элементам четвертой строки – элементы второй строки, умноженные на
; к элементам четвертой строки – элементы второй строки, умноженные на  ; к элементам пятой строки – элементы второй строки, умноженные на
; к элементам пятой строки – элементы второй строки, умноженные на 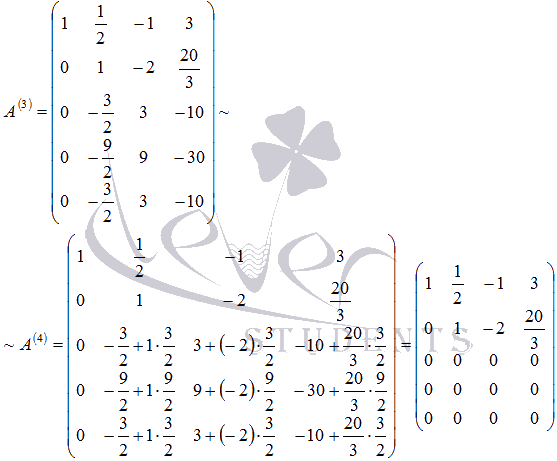
 .
.
 равен единице, поэтому не нужно производить умножение элементов первой строки на
равен единице, поэтому не нужно производить умножение элементов первой строки на  . Сделаем все элементы первого столбца, кроме первого, нулевыми:
. Сделаем все элементы первого столбца, кроме первого, нулевыми:
 :
:
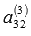 уже равен нулю.
уже равен нулю. , а
, а  , то поменяем местами третий и четвертый столбцы:
, то поменяем местами третий и четвертый столбцы:
 :
:
 разрешима тогда и только тогда, когда
разрешима тогда и только тогда, когда  , где
, где  — расширенная матрица, полученная из матрицы
— расширенная матрица, полученная из матрицы  приписыванием столбца
приписыванием столбца  [1].
[1]. такие, что
такие, что  . Следовательно, столбец
. Следовательно, столбец  матрицы
матрицы  .
. . Возьмём в матрице
. Возьмём в матрице  , то он же будет базисным минором и матрицы
, то он же будет базисным минором и матрицы  . Тогда, согласно теореме о базисномминоре, последний столбец матрицы
. Тогда, согласно теореме о базисномминоре, последний столбец матрицы 
 . Тривиальное, для тех, кто совсем не понял смысл прилагательного, значит, беспонтовое. Не академично, конечно, но зато доходчиво =) …Чего ходить вокруг да около, давайте выясним, нет ли у данной системы каких-нибудь других решений:
. Тривиальное, для тех, кто совсем не понял смысл прилагательного, значит, беспонтовое. Не академично, конечно, но зато доходчиво =) …Чего ходить вокруг да около, давайте выясним, нет ли у данной системы каких-нибудь других решений:
 , и, применяя обратный ход метода Гаусса, легко убедиться, что решение единственно.
, и, применяя обратный ход метода Гаусса, легко убедиться, что решение единственно. – 3 шт.).
– 3 шт.).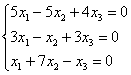



 , «сидящие на ступеньках» – главные, переменная
, «сидящие на ступеньках» – главные, переменная 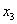 , которой не досталось «ступеньки» – свободная.
, которой не досталось «ступеньки» – свободная.

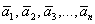 , каждый из которых является решением однородной системы, кроме того, решением также является линейная комбинация данных векторов
, каждый из которых является решением однородной системы, кроме того, решением также является линейная комбинация данных векторов 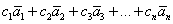 , где
, где 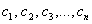 – произвольные действительные числа.
– произвольные действительные числа. фундаментальной системы рассчитывается по формуле:
фундаментальной системы рассчитывается по формуле:
 . Как его найти? Для этого свободной переменной нужно придать произвольное ненулевое значение. Проще всего, конечно же, выбрать
. Как его найти? Для этого свободной переменной нужно придать произвольное ненулевое значение. Проще всего, конечно же, выбрать  и получить:
и получить:  .
.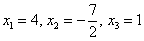 должны удовлетворять каждому уравнению системы, и будет не лишним в этом убедиться.
должны удовлетворять каждому уравнению системы, и будет не лишним в этом убедиться.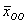 (подстрочный индекс расшифровывается «Общее Однородной»).
(подстрочный индекс расшифровывается «Общее Однородной»). , где
, где  (любое вещественное число)
(любое вещественное число)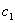 различные действительные значения, можно получить бесконечно много частных решений, например, если
различные действительные значения, можно получить бесконечно много частных решений, например, если  , то вектор частного решения однородного уравнения («Частное Однородной») равен:
, то вектор частного решения однородного уравнения («Частное Однородной») равен: , то есть набор переменных
, то есть набор переменных  удовлетворяет каждому уравнению системы.
удовлетворяет каждому уравнению системы.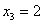 и из общего решения системы
и из общего решения системы 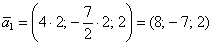
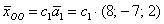 , где
, где 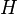 называется подмножество
называется подмножество 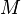 этого пространства вида
этого пространства вида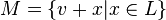
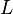 и вектора
и вектора  , то есть подмножество, полученное сдвигом каждого элемента из
, то есть подмножество, полученное сдвигом каждого элемента из 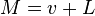
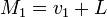 и
и 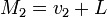 , то
, то 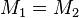 тогда и только тогда, когда и
тогда и только тогда, когда и 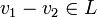 .
. (т.е.
(т.е. 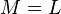 .
.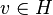 в определении
в определении 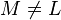 ) ортогональным подпространству
) ортогональным подпространству 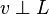 единственно.
единственно.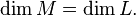 Для линейных многообразий
Для линейных многообразий  в
в  -мерном векторном пространстве или
-мерном векторном пространстве или 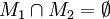 , или
, или