
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема (о виде общего решения неоднородной системы уравнений).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Решение неоднородной системы уравнений
Доказательство. Рассмотрим разность
Таким образом, показано, что указанная разность всегда является некоторым решением соответствующей однородной системы, что и доказывает теорему. Частное решение неоднородной системы обычно выделяют из ее общего решения, полагая в общем решении вектор произвольных постоянных
Пример. Решим методом Гаусса следующую систему уравнений:
Выпишем расширенную матрицу этой системы и выполним ее элементарные преобразования по методу Гаусса. Умножим первую строку последовательно на числа 3, 2, 1 и вычтем результаты из второй, третьей и четвертой строк:
Вычтем теперь последовательно из третьей и четвертой строк вторую строку, а вторую строку разделим на число 5. Мы получили ступенчатую матрицу
Примем за базисные неизвестные
Полученная система имеет единственное решение относительно базисных неизвестных
Запишем общее решение неоднородной системы, используя ее частное решение и фундаментальную систему решений, соответствующего однородного уравнения. Полагая в общем решении неоднородного уравнения, вектор произвольных постоянных
Далее положим в общем решении Окончательно, общее решение исходного неоднородного уравнения представляется в виде:
С помощью метода Гаусса можно эффективно вычислять обратную матрицу Пример. Вычислим по методу Гаусса матрицу, обратную к Специальная расширенная матрица в нашем случае имеет вид:
Далее выполняются элементарные преобразования над расширенной матрицей по полной схеме метода Гаусса:
Таким образом, в матрице
Правильность вычисления обратной матрицы всегда рекомендуется проверять непосредственно по ее определению 10. Изменение матрицы линейного преобразования при изменении базиса В предыдущем разделе мы установили, что как только в линейном пространстве выбран базис, то каждому линейному преобразованию соответствует матрица этого преобразования. Однако если выбрать в пространстве другой базис, то матрица преобразования, как правило, станет другой. Выясним, как эти матрицы связаны между собой. Пусть Предложение 19.1 Пусть
Доказательство. Пусть Определение 19.2 Две квадратных матрицы Следствие 19.1 Матрицы одного линейного преобразования, соответствующие разным базисам, подобны друг другу, и наоборот, если матрицы подобны, то они являются матрицами одного и того же преобразования в разных базисах. Пример 19.4 Пусть Пусть
Но выражение в последнем равенстве справа является координатным столбцом образа суммы векторов Пусть
то есть равен числу Очевидно, что примерами линейных преобразований могут служить тождественное преобразование, то есть преобразование, переводящее каждый вектор в себя, Легко проверяется, что для любого линейного преобразования
Матрица линейного преобразования В примере 19.4 было показано, что преобразование Пусть Запишем разложение вектора
Векторы
Подставим это выражение в равенство (19.2) и, используя предложение 14.3, изменим порядок суммирования
Это равенство означает, что Составим матрицу
Вычислим произведение матрицы
Мы видим, что
Это означает, что в выбранном базисе действие любого линейного преобразования сводится к умножению матрицы на координатный столбец вектора. Матрица Пример 19.5 Найдем матрицу линейного преобразования Выберем какой-нибудь базис
Следовательно, первый столбец матрицы
Второй столбец матрицы
Пример 19.6 Найдем матрицу линейного преобразования Из рисунка 19.7 видно, что вектор
Рис.19.7.Координаты образов базисных векторов при преобразовании поворота
Поэтому координатный столбец образа первого базисного вектора имеет вид
Преобразование матрицы линейного оператора при переходе к новому базису Пусть линейный оператор
: Xn → Xn в базисе e имеет матрицу A e. Найдем матрицу этого оператора A f в базисе f. Пусть C — матрица перехода от базиса e к базису f. Теорема. Преобразование матрицы оператора
при переходе от "старого" базиса e к "новому" базису f определяется формулой:
Доказательство. Рассмотрим произвольный вектор x и его образ y =
x. Обозначим координатные столбцы этих векторов: X e и Y e — в "старом" базисе e; X f и Y f — в "новом" базисе f. Тогда
и
Отсюда, используя формулы преобразования вектора, получаем
Сравнивая с выражением Y f = A f · X f, приходим к формуле (1), которую требовалось доказать. ¾¾¾¾ * * * Собственные значения и собственные векторы линейного преобразования.
Определение: Пусть L – заданное n- мерное линейное пространство. Ненулевой вектор A
При этом число l называется собственным значением (характеристическим числом) линейного преобразования А, соответствующего вектору
Определение: Если линейное преобразование А в некотором базисе
Это уравнение называется характеристическим уравнением, а его левая часть- характеристическим многочленом линейного преобразования А.
Следует отметить, что характеристический многочлен линейного преобразования не зависит от выбора базиса.
Рассмотрим частный случай. Пусть А – некоторое линейное преобразование плоскости, матрица которого равна
в некотором базисе Если преобразование А имеет собственный вектор с собственным значением l, то А
Т.к. собственный вектор
Полученное уравнение является характеристическим уравнением линейного преобразования А.
Таким образом, можно найти собственный вектор
Понятно, что если характеристическое уравнение не имеет действительных корней, то линейное преобразование А не имеет собственных векторов. Следует отметить, что если Действительно,
Т.к. характеристическое уравнение может иметь два различных действительных корня l1 и l2, то в этом случае при подстановке их в систему уравнений получим бесконечное количество решений. (Т.к. уравнения линейно зависимы). Это множество решений определяет две собственные прямые.
Если характеристическое уравнение имеет два равных корня l1 = l2 = l, то либо имеется лишь одна собственная прямая, либо, если при подстановке в систему она превращается в систему вида:
Пример. Найти характеристические числа и собственные векторы линейного преобразования с матрицей А =
Запишем линейное преобразование в виде: Составим характеристическое уравнение: l2 - 8l + 7 = 0; Корни характеристического уравнения: l1 = 7; l2 = 1; Для корня l1 = 7: Из системы получается зависимость: x1 – 2x2 = 0. Собственные векторы для первого корня характеристического уравнения имеют координаты: (t; 0,5t) где t - параметр.
Для корня l2 = 1: Из системы получается зависимость: x1 + x2 = 0. Собственные векторы для второго корня характеристического уравнения имеют координаты: (t; -t) где t - параметр.
Полученные собственные векторы можно записать в виде:
Пример. Найти характеристические числа и собственные векторы линейного преобразования с матрицей А =
Запишем линейное преобразование в виде:
Составим характеристическое уравнение: l2 - 4l + 4 = 0;
Корни характеристического уравнения: l1 = l2 = 2; Получаем: Из системы получается зависимость: x1 – x2 = 0. Собственные векторы для первого корня характеристического уравнения имеют координаты: (t; t) где t - параметр.
Собственный вектор можно записать:
Рассмотрим другой частный случай. Если где l - собственное значение (характеристическое число) преобразования А.
Если матрица линейного преобразования А имеет вид:
Характеристическое уравнение: Раскрыв определитель, получим кубическое уравнение относительно l. Любое кубическое уравнение с действительными коэффициентами имеет либо один, либо три действительных корня. Тогда любое линейное преобразование в трехмерном пространстве имеет собственные векторы.
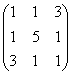
Пример. Найти характеристические числа и собственные векторы линейного преобразования А, матрица линейного преобразования А =
Составим характеристическое уравнение:
(1 - l)((5 - l)(1 - l) - 1) - (1 - l - 3) + 3(1 - 15 + 3l) = 0 (1 - l)(5 - 5l - l + l2 - 1) + 2 + l - 42 + 9l = 0 (1 - l)(4 - 6l + l2) + 10l - 40 = 0 4 - 6l + l2 - 4l + 6l2 - l3 + 10l - 40 = 0 -l3 + 7l2 – 36 = 0 -l3 + 9l2 - 2l2 – 36 = 0 -l2(l + 2) + 9(l2 – 4) = 0 (l + 2)(-l2 + 9l - 18) = 0
Собственные значения: l1 = -2; l2 = 3; l3 = 6;
1) Для l1 = -2:
Если принять х1 = 1, то
Собственные векторы:
2) Для l2 = 3:
Если принять х1 = 1, то
Собственные векторы:
3) Для l3 = 6:
Если принять х1 = 1, то
Собственные векторы: Пример. Найти характеристические числа и собственные векторы линейного преобразования А, матрица линейного преобразования А =
Составим характеристическое уравнение:
-(3 + l)((1 - l)(2 - l) – 2) + 2(4 - 2l - 2) - 4(2 - 1 + l) = 0 -(3 + l)(2 - l - 2l + l2 - 2) + 2(2 - 2l) - 4(1 + l) = 0 -(3 + l)(l2 - 3l) + 4 - 4l - 4 - 4l = 0 -3l2 + 9l - l3 + 3l2 - 8l = 0 -l3 + l = 0 l1 = 0; l2 = 1; l3 = -1;
Для l1 = 0:
Если принять х3 = 1, получаем х1 = 0, х2 = -2 Собственные векторы Две системы, множества решений которых совпадают, называются эквивалентными или равносильными (совпадение множеств решений означает, что каждое решение первой системы является решением второй системы, и каждое решение второй системы является решением первой) 11. Согласно теории множеств, любую геометрическую фигуру следует рассматривать как множество всех принадлежащих ей точек. Таким образом, всякая геометрическая фигура есть не пустое множество.
Евклидово пространство и его свойства В символической форме эти выражения могут быть записаны A ∈ α; B ∈ a Аксиомы инцидентности или отношения принадлежности между элементами евклидова пространства могут быть выражены следующими предложениями: 1. Если точка A принадлежит прямой a, а прямая a принадлежит плоскости α, то точка A принадлежит плоскости α
2. Две различные точки A и B всегда принадлежат одной и той же и только одной прямой a или каждой прямой a принадлежат, по крайней мере, две точки A и B
3. Три различные точки A, B и C, не принадлежащие одной прямой, принадлежат одной и той же и только одной плоскости
4. Если две точки A и B, принадлежащие прямой a, принадлежат плоскости α, то и прямая a принадлежит плоскости α
Кроме отмеченных предложений, могут быть сформулированы и другие предложения принадлежности для элементов евклидова пространства: 5. Две прямые, принадлежащие одной плоскости, могут принадлежать одной точке, но этого может и не быть. 6. Две плоскости могут принадлежать одной и той же прямой, но этого может и не быть. 7. Плоскость и не принадлежащая ей прямая могут принадлежать одной точке, но этого может и не быть. Последние три предложения по существу перефразируют аксиому о параллельности:
Определителем Грама (грамианом) системы векторов
где Матрица Грама возникает из следующей задачи линейной алгебры: Пусть в евклидовом пространстве | ||||||||||||||||||||||||||||||||||
|
| Поделиться: |

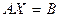 всегда может быть представлено как сумма общего решения соответствующей однородной системы и произвольного частного решения неоднородной системы
всегда может быть представлено как сумма общего решения соответствующей однородной системы и произвольного частного решения неоднородной системы .
. между любым решением
между любым решением 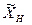 неоднородной системы
неоднородной системы 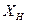 той же системы. Используя линейные свойства матриц, получим
той же системы. Используя линейные свойства матриц, получим .
. равным нулевому вектору
равным нулевому вектору 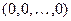 в пространстве арифметических векторов размерности
в пространстве арифметических векторов размерности  :
: .
.
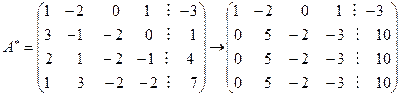
 , соответствующую этапу прямого хода метода Гаусса
, соответствующую этапу прямого хода метода Гаусса .
. , а за свободные неизвестные
, а за свободные неизвестные  . Отбросив в ступенчатой матрице
. Отбросив в ступенчатой матрице 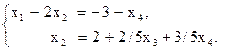
 . Подставляя выражение для
. Подставляя выражение для  в первое уравнение системы, получим окончательно общее решение неоднородной системы в виде:
в первое уравнение системы, получим окончательно общее решение неоднородной системы в виде: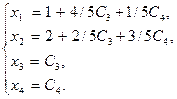
 равным нулевому вектору
равным нулевому вектору  , получим частное решение неоднородной системы в виде
, получим частное решение неоднородной системы в виде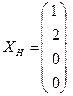 .
.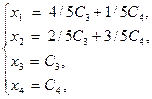 соответствующего однородного уравнения вектор произвольных постоянных
соответствующего однородного уравнения вектор произвольных постоянных 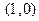 ,
, 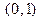 . В результате получим фундаментальную систему решений приведенного однородного уравнения в виде
. В результате получим фундаментальную систему решений приведенного однородного уравнения в виде  .
. .
.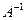 . Из теоремы Крамера следует, что обратные матрицы существуют только для невырожденных матриц и находятся единственным образом, какой бы способ не использовался для их вычисления. Количество арифметических операций при обращении матрицы порядка
. Из теоремы Крамера следует, что обратные матрицы существуют только для невырожденных матриц и находятся единственным образом, какой бы способ не использовался для их вычисления. Количество арифметических операций при обращении матрицы порядка  по методу Гаусса равно числу
по методу Гаусса равно числу 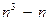 и является наименьшим по сравнению с другими точными методами. Для построения обратной матрицы
и является наименьшим по сравнению с другими точными методами. Для построения обратной матрицы  сначала составляют специальную расширенную матрицу
сначала составляют специальную расширенную матрицу  . Далее выполняются элементарные преобразования над расширенной матрицей по полной схеме метода Гаусса. В результате матрица
. Далее выполняются элементарные преобразования над расширенной матрицей по полной схеме метода Гаусса. В результате матрица  . В преобразованной матрице
. В преобразованной матрице  , составленное относительно неизвестных нам элементов матрицы
, составленное относительно неизвестных нам элементов матрицы 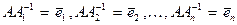 . Правые части этих систем состоят из канонических арифметических вектор – столбцов
. Правые части этих систем состоят из канонических арифметических вектор – столбцов  , а неизвестными являются столбцы
, а неизвестными являются столбцы  искомой матрицы
искомой матрицы  по методу Гаусса, а в преобразованной матрице
по методу Гаусса, а в преобразованной матрице  .
. .
.

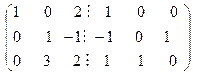


 =
=  .
. , выбирая для контроля любое из равенств.
, выбирая для контроля любое из равенств. --
--  -мерное линейное пространство,
-мерное линейное пространство,  и
и  -- два базиса в этом пространстве. Первый из них назовем "старым", а второй -- "новым". Пусть
-- два базиса в этом пространстве. Первый из них назовем "старым", а второй -- "новым". Пусть  -- матрица перехода 19.1.4 а от старого базиса к новому.
-- матрица перехода 19.1.4 а от старого базиса к новому. -- линейное преобразование пространства
-- линейное преобразование пространства  и
и  -- матрицы этого преобразования в старом и новом базисе соответственно. Тогда
-- матрицы этого преобразования в старом и новом базисе соответственно. Тогда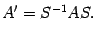
 -- произвольный вектор пространства
-- произвольный вектор пространства  -- его образ, то есть
-- его образ, то есть  . Пусть
. Пусть 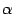 и
и  -- координатные столбцы векторов
-- координатные столбцы векторов  ,
,  -- в новом. Тогда в силу формулы (19.3)
-- в новом. Тогда в силу формулы (19.3) 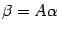 . По предложению 18.5 имеем
. По предложению 18.5 имеем  ,
,  . Подставим эти выражения в предыдущую формулу, получаем
. Подставим эти выражения в предыдущую формулу, получаем  . Откуда
. Откуда  . С другой стороны, в силу формулы (19.3) в новом базисе
. С другой стороны, в силу формулы (19.3) в новом базисе  . Сравнивая это равенство с предыдущим, получаем
. Сравнивая это равенство с предыдущим, получаем  .
. и
и  одного порядка называются подобными, если существует такая невырожденная матрица
одного порядка называются подобными, если существует такая невырожденная матрица  .
.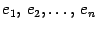 . Тогда у любого вектора
. Тогда у любого вектора  . Пусть
. Пусть  является вектором, координатный столбец которого равен
является вектором, координатный столбец которого равен  (справа стоит произведение матрицы
(справа стоит произведение матрицы  и
и  -- координатные столбцы
-- координатные столбцы 
 . Следовательно,
. Следовательно,  .
. -- произвольное число. Тогда координатный столбец вектора
-- произвольное число. Тогда координатный столбец вектора 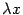 равен
равен  , координатный столбец образа вектора
, координатный столбец образа вектора
 . Тем самым мы доказали, что преобразование
. Тем самым мы доказали, что преобразование  , и нулевое преобразование, переводящее каждый вектор в нуль,
, и нулевое преобразование, переводящее каждый вектор в нуль,  .
. . Действительно, в силу второго из равенств (19.1)
. Действительно, в силу второго из равенств (19.1)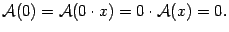
 . Для образа этого вектора получим
. Для образа этого вектора получим
 имеют какие-то координатные столбцы, обозначим их
имеют какие-то координатные столбцы, обозначим их  ,
,  ,...,
,...,  соответственно. В этой записи первый индекс показывает номер координаты, а второй индекс -- номер вектора. Соответственно,
соответственно. В этой записи первый индекс показывает номер координаты, а второй индекс -- номер вектора. Соответственно,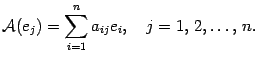

 -той координатой вектора
-той координатой вектора 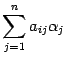 .
.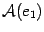 ,...,
,..., 



 . Тогда
. Тогда
 . Аналогично
. Аналогично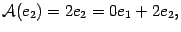
 . В итоге
. В итоге
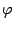 возьмем равным
возьмем равным  . В качестве базиса возьмем привычный ортонормированный базис i, j.
. В качестве базиса возьмем привычный ортонормированный базис i, j. имеет координаты
имеет координаты  и
и  .
.
 . Координаты образа второго базисного вектора равны
. Координаты образа второго базисного вектора равны 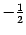 и
и  , его координатный столбец имеет вид
, его координатный столбец имеет вид 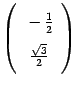 . В итоге получаем, что в базисе i, j матрица поворота на угол
. В итоге получаем, что в базисе i, j матрица поворота на угол 
 L называется собственным вектором линейного преобразования А, если существует такое число l, что выполняется равенство:
L называется собственным вектором линейного преобразования А, если существует такое число l, что выполняется равенство: .
. .
. ,
,  ,…,
,…,  имеет матрицу А =
имеет матрицу А =  , то собственные значения линейного преобразования А можно найти как корни l1, l2, …,lnуравнения:
, то собственные значения линейного преобразования А можно найти как корни l1, l2, …,lnуравнения:
 . Тогда преобразование А может быть задано формулами:
. Тогда преобразование А может быть задано формулами: ;
; 
 .
. или
или 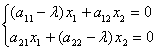
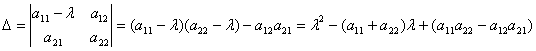
 . Если учесть, что векторы имеют одно начало, то эти векторы образуют так называемое собственное направление или собственную прямую.
. Если учесть, что векторы имеют одно начало, то эти векторы образуют так называемое собственное направление или собственную прямую. . Эта система удовлетворяет любым значениям х1 и х2. Тогда все векторы будут собственными, и такое преобразование называется преобразованием подобия.
. Эта система удовлетворяет любым значениям х1 и х2. Тогда все векторы будут собственными, и такое преобразование называется преобразованием подобия. .
.




 .
.


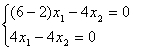
 .
. , то
, то ,
, , то
, то 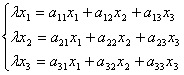

 .
.


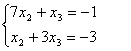 Þ х2 = 0; x3 = -1;
Þ х2 = 0; x3 = -1;
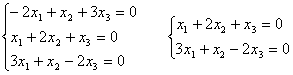
 Þ х2 = -1; x3 = 1;
Þ х2 = -1; x3 = 1;
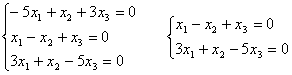
 Þ х2 = 2; x3 = 1;
Þ х2 = 2; x3 = 1;
 .
.

 ×t, где t – параметр.
×t, где t – параметр.

 в евклидовом пространстве называется определитель матрицы Грама этой системы:
в евклидовом пространстве называется определитель матрицы Грама этой системы:
 — скалярное произведение векторов
— скалярное произведение векторов  и
и  .
. система векторов
система векторов  . Зная, чему равны скалярные произведения вектора
. Зная, чему равны скалярные произведения вектора  из
из 


