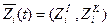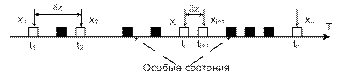Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая математическая модель системы. Классификация параметров модели.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
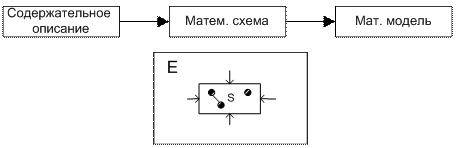
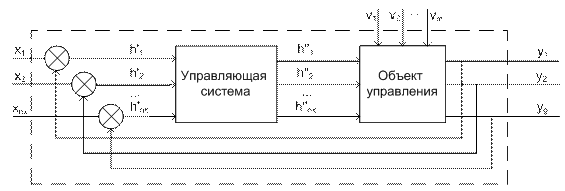
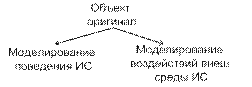
На основе постановки задачи строится концептуальная модель системы оригинала. Концепт модель должна в первом приближении описать моделируемую систему. На этом этапе происходит выделение функциональных блоков системы, описание их взаимодействия, формируется первичный набор параметров системы. На концептуальные модели не существует стандартов, тем не менее концепт модель м/б построена с привлечением ряда описательных стандартов (UML, IDEF). Основные требование к концепт модели: четкость описания, понятность и доступность описания для аудитории. На этапе содержательного описания требуется четко выделить саму систему и объекты окружающей среды. На втором этапе происходит выбор математической схемы. Третий этап – построение мат модели на основании выбранной математической схемы. Все параметры объекта оригинала классифицируются по 4 осн признакам: - параметры входных воздействий – специальная группа пар-ров, варьируя значения к-рой исследователь моделирует поведение системы в контексте поставленных задач. xi ÎX, - пар-ры воздействия внеш среды – при моделировании объекта оригинала заменяется моделью, чье поведение исследуется в некой внеш модельной среде. При построении концепт модели пар-ры объекта заместителя и внеш среды строго разграничены, тем не менее между ними может существовать связь. Параметры внеш среды, к-рые непосредственно взаимодействуют с параметрами модели, определяют множество пар-ров воздействия внеш среды. vl ÎV, - внутренние пар-ры системы – описывают структуру системы и природу взаимодействия структуры блоков. hk ÎH, - выходные характеристики системы являются исследуемыми пар-рами системы, их значение вычисляются на основании выбранных X, V, H пар-ров и построенных мат моделей. yj ÎY, Все пар-ры м/б управляемые и неуправляемые. Управляемые пар-ры – пар-ры, к-рые м/б изменены исследователем в процессе эксперимента. Все параметры могут иметь детерминированный и стохастический характер. К независимым (экзогенным) переменным относятся:
Зависимые (эндогенные) переменные: Динамическая и статическая модели объектов. Реализация динамических и статических моделей.
Реализация динамической и статической модели: - аналитически - графически - таблично - через состояние Аналитические модели строятся с применением математических операций. Модели состояния м/б частным случаем аналитических моделей. Применение через состояние удобно применять, если акцент делается на детальное описание внутр параметров системы.
Состояние системы. Множество состояний системы. Детерминированная и стохастическая модели системы.
x(t) – входные воздействия h(t) – внутренние параметры v(t) – воздействия внеш среды
T=mΔt, m – число интервалов дискретизации. Математическая модель(стохастическая): математические связи между
Математическая модель (детерминированная):
Схемы общего вида. Типовые схемы. Классификация типовых схем. Типовые схемы: - непрерывно-детерминированные (D-схемы). Диф. уравнения. - дискретно-детерминированные (F-схемы). Конечные автоматы. - дискретно-стохастические (Р-схемы). Вероятностные автоматы. - непрерывно-стохастические (Q-схемы). Системы массового обслуживания (СМО). - сетевые (N-схемы) Сети Петри - универсальные (A-схемы) Комбинированные системы. Типовые математические системы адаптированы для решения конкретных классов задач и м/б использованы на практике. Схемы делятся на 2 вида: 1. Схемы общего вида: - высокая степень общности - возможность описания произвольной системы 2. Типовые схемы: - простота, наглядность - практичность применения - возможность описания ограниченного класса систем
D-схемы.
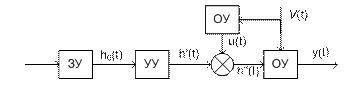
D-схемы применяются для моделирования систем, характеристики к-рых меняются с течением времени под воздействием непрерывных потоков входной информации и воздействия окружающей среды. Такие системы должны исключать случайные процессы. Класс систем-оригиналов: системы автоматического управления. Задача: поддержание F без участие человека. Принцип управления: - принцип разомкнутого управления - принцип компенсации - принцип обратной связи Принцип разомкнутого управления
«+»: простота, системность «-»: для оптимизации системы необходимо построить новую схему, к-рая подвергается анализу выходных хар-тик. Система самостоятельно не может адаптироваться к возможным изменениям значений характеристик. Принцип компенсации
«+»: - возможность адаптации к изменяющимся внеш условиями - высокая скорость реагирования на изменение внеш условий «-»: невозможно отслеживать всех возможных внеш воздействий. Принцип обратной связи
«+»: возможность учета всех видов воздействия внеш среды «-»: снижение времени реакции на изменение воздействия внеш среды по сравнению с предыдущими схемами. На практике использует комбинированный подход, при к-ром все внеш воздействия разделяются на 2 группы: - воздействия, к-рые требуют быстрой реакции САУ - все остальные воздействия; при обработке изменения параметров событий первой группы используется принцип компенсации, для отслеживания изменений второй группы используется принцип обратной связи.
Идеальная система: h'(t)=0
Динамический процесс в САУ: F (y, y', y'',…,y(n), h, h', h'',…,h(m), v, v', v'',…,v(k))=0
F-схемы.
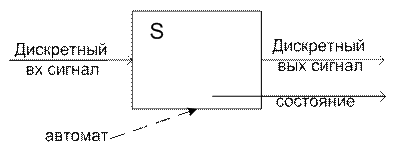
С помощью F-схем целесообразно моделировать системы с четным кол-вом состояний и дискретным характером вход сигнала. Формализация: F=<z, x, y, j,y,z0> z – множество внутр состояний х – мн-во входных состояний у – мн-во выходных сигналов j - функция переходов y - функция выходов z0 – начальное состояние
F-схема: - по зависимости от вх сигнала: *Автомат Мили *Автомат Мура - по наличию памяти * с памятью * без памяти - по кол-ву вх сиганлов и состояний: *конечный автомат - по хар-ру отсчета дискретного времени: *синхронный *асинхронный Применение:
Р-схемы. Вероятностный автомат (ВА) - это дискретный потактный преобразователь информации с памятью, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть описано статистически. Схемы вероятностных автоматов (Р-схем) применяются: - в проектировании дискретных систем, проявляющих статистически закономерное случайное поведение; - в определении алгоритмических возможностей систем; - в обосновании границ целесообразности их использования; - в решении задач синтеза по выбранному критерию дискретных стохастических систем, удовлетворяющих заданным ограничениям. Математическое понятие Р-автомата формируется на понятиях, введенныхдля F-автомата.
Формализация:
bkj – вероятности перехода автомата в состояние zk и появление на выходе сигнала yj, если он находился в состоянии zi и на его вход в этот момент времени поступил сигнал xl. Применение:
N-схемы.
B – множество позиций D – мн-во переходов I – вход функция О – обратная функция I(di)={biÎB|I(bi,dj)=1} O(di)={ biÎB|O(dj, bi)=1} i=1,n; j=1,m; n=|B|, m=|D|
если система представима в виде графа, включающего 2 типа вершин(элементы позиций и элементов переходов) и определены 2 типа связей (обрат и вход функция), то целесообразно использовать формализм сетей Петри. Множество входных функций определяет множество связей из элементов переходов в элементы позиций. Динамическими объектами сетей Петри являются подмодели сети Петри, описывающие процессы системы, выполняемые параллельно, между к-рыми возникают потоки данных и потоки управляющих сигналов. Все потоки возникают при выполнении опред условий, что позволяет их трактовать в качестве причинно-следств связей. Маркированная (размеченная) сеть: Nm=<B,D,I,O,M> M: B®{0,1,2,3,…} Условие срабатывания перехода dj: biÎI(dj) M(bi)³1 Процесс перехода M(bi) ®M’(bi): M’(bi)= M(bi)-I(dj)+O(dj) Отражение временных параметров: временные сети, Е-сети, сети Мерлина. Для придания сети Петри динамических свойств вводится дополнительное множество (мн-во маркеров сети). Каждый элемент маркера показывает кол-во динамич объектов, ассоциируемых с каждым элементом множ-ва позиций. Элемент множества переходов считается готовым к переходу, если: - для него существует не пустое множество значений функции ввода. - связанные с ним элементы позиций (источники динамических объектов) имеют значение маркера, отличного от нуля В процессе перехода происходит: - уменьшение значения маркера связанного с элементом позиции (источником динамических объектов) - увеличение маркера, связанного с элементом позиции (приемником динамических объектов). N-схемы м/б применены при описании событийно-ориентированных моделей.
Q-схемы.
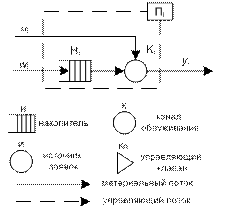
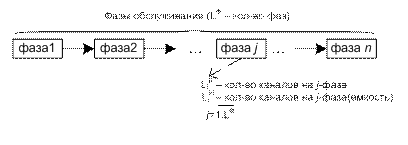
w – поток событий прихода заявок (на накопитель Н) u – поток событий обслуживаний (на К) у – выходной поток Системы массового обслуживания (СМО) являются непрерывно-стохастическими системами. При описании СМО м/б использован формализм Q-схем. СМО: - по кол-ву единиц обсл-я (параллельное соед-е приборов): много- и одноканальные - по кол-ву этапов обсл-я(послед. соед. приборов): много- и однофазные - по св-вам каналов(кол-во способов обсл-я): неоднородны и однородные.
Если СМО включает один прибор, то такая СМО является однофазной одноканальной системой. Если СМО включает несколько приборов, соединенных паралл-но к-рые позволяют вести парал-ную обработку нескольких транзактов и в совокупности м/б рассмотрены как одно устр-во, включающее несколько парал-ных каналов обслуживания, то такие системы явл-ся многоканальными. Если несколько приборов соединены послед-но, то транзакты обслуживаются послед-но в каждом приборе (имеют несколько фаз обслуживания), то система является многофазной. Если функционирование канала не меняется на протяжении времени функционирования системы, то система является однородной. Иначе, неоднородная. Поток событий. Однородный поток событий: моменты поступления: 0£t1£t2£…£tn£… интервалы поступлений: t1=t1; t2=t2 -t1;…. Неоднородный поток событий: {ti; fi} Детерминированный поток: t = const Случайный поток событий: t ¹ const Поток с ограниченным последствием: интервалы поступлений независимы. Типы поток событий: - стационарный поток событий (Р не зависти от t); - одинарный поток событий (P(k>1,t, t) ~0); - поток без последствия (P не зависит от n (m не зависит от n)); Простой (пуассоновский) поток: - стационарный - ординарный - без последствий
Поток является стационарным, если он определяется интервалом времени наблюдения и не определяется опред-м моментом времени. Поток событий является ординарным, если в сколько угодно малом промежутке времени возникает только одно событие. Поток наз-ся поток без последствий, если кол-во наблюдаемых событий не одном интервале времени не зависит от кол-ва событий, наблюдаемых на др. интервале времени (интервалы времени не пресекаются) Интенсивность потока событий.
N–число событий за время наблюдения. Интенсивность потока соб-й: l=N/Тн Вероятность появления n событий на интервале [t, t+t]:
Канал обслуживания: - по дисциплине обслуживания: - FIFO - LIFO - по приоритету - по закону распределения - по действию при занятом канале: - отказ - ожидание с ограничением по времени или по длине очереди - ожидание Состояние прибора {кол-во заявок в накопителе, кол-во заявок в очерди}
Параметры Q-схемы:
Системы с потерями: LiН=0 Системы с ожиданием: LiН®¥ Дисциплины обслуживания: - алгоритм выбора из очереди - алгоритм обслуживания
Приоритет заявки: - по процессу захвата канала: - абсолютный - относительный - по процессу формирования - статический - динамический Приоритет транзакта является абсолютным, если транзакт может осуществить прерывание обслуживание др. транзакта. Иначе, относительный. Транзакт с максимальным приоритетом гарантированно первым выбирается из очереди. Приоритет явл-ся статическим, если его значение задается до моделирования и более не меняется. Приоритет динамический, если значения зависят от св-в Q-схемы и в процессе моделирования м/б изменены. Алгоритм функционирования приборов: - правила переполнения канала/накопителя - правила ухода по истечению времени - правила выбора маршрута ухода - правила блокировки каналов
Формализация: Q = <W, U, H, Z, R, A> W – поток событий прихода заявок U – поток событий обслуживания заявок Н – множ-во внутренних параметров системы Z – множ-во состояний системы R – оператор сопряжения приборов A – оператор алгоритмов обслуживания Способы исследования: - аналитические модели - компьютерные модели
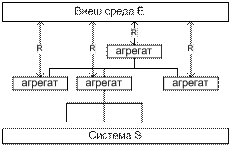
А-схемы А-схема (комбинированная) позволяет формализовать системы, включающие непрерывные, дискретные, детерминированные, стохастические компоненты. Нотация А-схем позволяет описать алгоритм функционирования систем. Требования: - адекватное математическое описание - основа для построения алгоритмов - основа для аналитического исследования
R - оператор сопряжения. Система в терминах А-схем представляет собой совокупность агрегатов(функциональных объектов), характеризуемых вход и выход каналами и алгоритмами функционирования. Вшен среда также представляется по средствам агрегатов. А–схемы поддерживает иерархическое разбиение агрегатов (от общего к частному). Взаимодействие между агрегатами описывается оператором сопряжения R. Оператор R задает взаимооднозначное соответствие между агр.–источником и агр.-приемником сигнала и определяет канал передачи данных и управляющие сигналы.
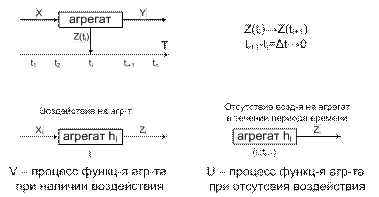
В процессе наблюдения за А-схемой происходит отслеживание состояния всех агр-ов. В общем случае интервал времени между соседними состояния агрегата м/б бесконечно малым. Выделяют 2 режима функционирования агрегата: при наличии и отсутствии внеш воздействий. Состояние в момент времени t0: Z0=Z(t0) Состояние при наличии сигнала в момент tn: Z(tn)=V[t, tn, Z(tn-1),xn] Состояние, если в течение (tn, tn+1) на было сигналов: Z(t)=U[t, tn, Z(tn)] F(V,U) – оператор перехода агр-ов в новые состояния.
V □ - процесс функционирования при регистрации сигнала U ■– проесс функционирования при отсутствии сигнала. Скачек состояния в особый момент времени: Z(tδ)=W[tδ, Z(tδ)] Скачек состояния в момент выдачи вых сигнала: y =G[tδ, Z(tδ)] Z(Y) – подмножество состояний выдачи вых сигнала; Z(tδ) Î Z(Y) А-схема описыавется 2 типами состояний: - состояния, возникающие под воздействием внеш сигнала - состояния, возникающие в процессе функционирования агр-та во внеш среде (состояния особых моментов). Вводятся дополнительные операторы для определения скачка состояний в особый момент W и оператор формирования отклика G. Формализация: A = <T, X, Y, Z, Z(Y), H> Операторы V, U, W, G Взаимодействие: - сигналы - сигнал - конченый набор характеристик - элементарные сигналы передаются мгновенно независимо по элементарным каналам - вход – один элементарный канал - выход – один и более элементарных каналов. Взаимодействие между агрегатами происходит с помощью сигналов. Каждый сигнал описывает-ся конечным набором характеристик. Выделяют элементарные и сложные сигналы. Слож сигналы должны быть дополнительно обработаны. Существует ограничение для вход и выход каналов агрегата.
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 692; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.30.153 (0.011 с.) |

 .
.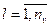 .
.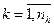 .
.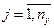 .
.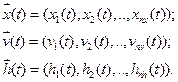
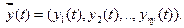

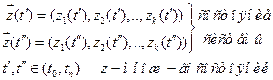

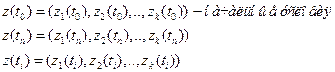

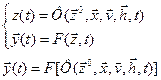

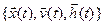
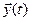 и
и 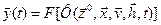
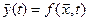
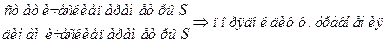
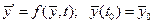
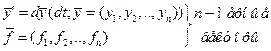
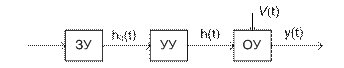
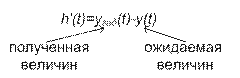

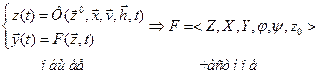


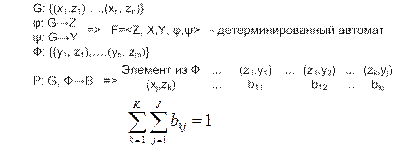
 Сети Петри N =< B, D, I, O >
Сети Петри N =< B, D, I, O >