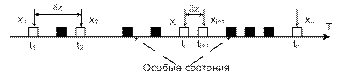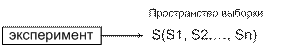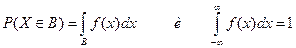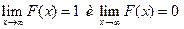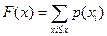Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование как метод научного познания. Процессы получения и обработки информации. Формирование и проверка гипотез.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Моделирование как метод научного познания. Процессы получения и обработки информации. Формирование и проверка гипотез.
Объект исследования представляет собой некую сущность (элемент, система, компонент и т.д.), о которой необходимо получить сведения(св-ва, характеристики, законы функционирования и т.д.). В общем случае на основании этих сведений формируется шаблон воздействия на объекты с целью достижения определенного эффекта(улучшение характеристик, выявление срытых механизмов функционирования и т.д.).
Изначально исследователь имеет min объем данных об исследуемом объекте. Кроме того, исследователь обладает информацией об окружающей среде данного объекта. На основании этой первичной информации исследователь формирует ряд гипотез относительно того как рассматриваемый объект может взаимодействовать с окружающей средой и к чему это может привести. По сформулированной гипотезе происходит расширение по данным об объекте и организует расширенный эксперимент. На основании экспериментальных данных осуществляется проверка первичных гипотез.
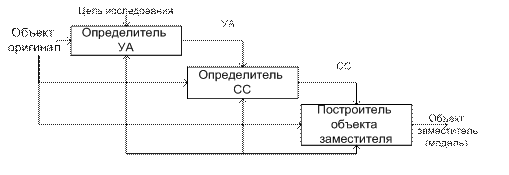
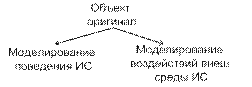
Объект оригинал. Объект заместитель. Уровень абстрагирования. Существенность сходства. Воздействие и отклик.
В большинстве случаев исследуемый объект не может быть изучен напрямую (сложность объекта, удаленность объекта от исследователя, стоимость проводимых исследований). В этом случае для исследования св-в объекта создается объект заместитель, обладающий всеми необходимыми св-вами, что и объект оригинал и исключающий все недостатки. В зависимости от сложности объекта оригинала исследования могут проводиться по множеству направлений и преследовать множество целей. Объект заместитель создается в зависимости от направления и цели исследования. В общем случае объект оригинал моет иметь множество объектов заместителей. Построение объекта заместителя происходит в 2 этапа: 1) определение уровня абстрагирования(определение подмножества характеристик объекта оригинала, которые необходимо передать в объект-заместитель) 2) определение степени схожести (определение степени соответствия двух объектов по воспринимаемым человеком характеристикам или по природе) Определяется класс моделей, который является текущим объектом заместителем.
Теория моделирования – теория замещения ОО на ОЗ.
При повторении объекта заместителя всегда возникает задача оценки её адекватности объекту оригиналу. Существует множество методов оценки адекватности: - проведение предварительных экспериментов с объектом заместителем для установления степени схожести выходной информации ОЗ и выходной информации ОО. - применение больших массивов информации функционирования ОО. - применение моделей-эталонов. При проведении предварительных экспериментов формируется воздействие на ОО и на ОЗ. Поскольку ОЗ и ОО являются объектами разной природы необходимо сформировать воздействие на ОЗ. Далее происходит чтение откликов, отклик ОЗ сразу формализован. Необходимо формализовать отклики от ОО. Используя методы математической статистики устанавливается степень адекватности модели ОО. Воздействие -действие, направленное на систему и определяющее ее переход от одного состояния к другому, изменяющее ее качество в том или ином направлении; может быть двух видов: целенаправленное и возмущающее. Отклик — выходная (эндогенная) переменная, характеризующая систему, изучаемую в эксперименте. Проблемы моделирования систем. 1. Выявление важных изучаемых свойств 2. Идентификация реальных объектов 3. Выбор типа модели 4. Построение модели 5. Оценка адекватности модели 6. Машинная реализация модели 7. Организация взаимодействия пользователя с моделью в процессе моделирования 8. Проверка правильности полученных результатов 9. Выявление закономерностей 10. Эргономика систем моделирования 11. Надежность средств моделирования
D-схемы.
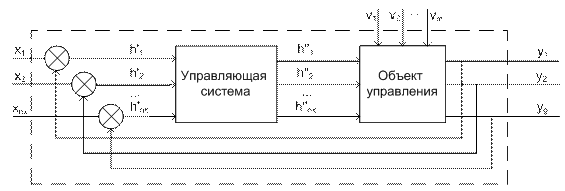
D-схемы применяются для моделирования систем, характеристики к-рых меняются с течением времени под воздействием непрерывных потоков входной информации и воздействия окружающей среды. Такие системы должны исключать случайные процессы. Класс систем-оригиналов: системы автоматического управления. Задача: поддержание F без участие человека. Принцип управления: - принцип разомкнутого управления - принцип компенсации - принцип обратной связи Принцип разомкнутого управления
«+»: простота, системность «-»: для оптимизации системы необходимо построить новую схему, к-рая подвергается анализу выходных хар-тик. Система самостоятельно не может адаптироваться к возможным изменениям значений характеристик. Принцип компенсации
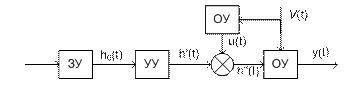
«+»: - возможность адаптации к изменяющимся внеш условиями - высокая скорость реагирования на изменение внеш условий «-»: невозможно отслеживать всех возможных внеш воздействий. Принцип обратной связи
«+»: возможность учета всех видов воздействия внеш среды «-»: снижение времени реакции на изменение воздействия внеш среды по сравнению с предыдущими схемами. На практике использует комбинированный подход, при к-ром все внеш воздействия разделяются на 2 группы: - воздействия, к-рые требуют быстрой реакции САУ - все остальные воздействия; при обработке изменения параметров событий первой группы используется принцип компенсации, для отслеживания изменений второй группы используется принцип обратной связи.
Идеальная система: h'(t)=0
Динамический процесс в САУ: F (y, y', y'',…,y(n), h, h', h'',…,h(m), v, v', v'',…,v(k))=0
F-схемы.
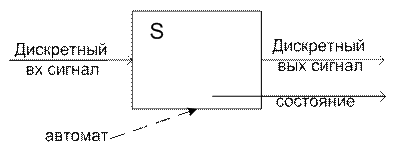
С помощью F-схем целесообразно моделировать системы с четным кол-вом состояний и дискретным характером вход сигнала. Формализация: F=<z, x, y, j,y,z0> z – множество внутр состояний х – мн-во входных состояний у – мн-во выходных сигналов j - функция переходов y - функция выходов z0 – начальное состояние
F-схема: - по зависимости от вх сигнала: *Автомат Мили *Автомат Мура - по наличию памяти * с памятью * без памяти - по кол-ву вх сиганлов и состояний: *конечный автомат - по хар-ру отсчета дискретного времени: *синхронный *асинхронный Применение:
Р-схемы. Вероятностный автомат (ВА) - это дискретный потактный преобразователь информации с памятью, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть описано статистически. Схемы вероятностных автоматов (Р-схем) применяются: - в проектировании дискретных систем, проявляющих статистически закономерное случайное поведение; - в определении алгоритмических возможностей систем; - в обосновании границ целесообразности их использования; - в решении задач синтеза по выбранному критерию дискретных стохастических систем, удовлетворяющих заданным ограничениям. Математическое понятие Р-автомата формируется на понятиях, введенныхдля F-автомата.
Формализация:
bkj – вероятности перехода автомата в состояние zk и появление на выходе сигнала yj, если он находился в состоянии zi и на его вход в этот момент времени поступил сигнал xl. Применение:
N-схемы.
B – множество позиций D – мн-во переходов I – вход функция О – обратная функция I(di)={biÎB|I(bi,dj)=1} O(di)={ biÎB|O(dj, bi)=1} i=1,n; j=1,m; n=|B|, m=|D|
если система представима в виде графа, включающего 2 типа вершин(элементы позиций и элементов переходов) и определены 2 типа связей (обрат и вход функция), то целесообразно использовать формализм сетей Петри. Множество входных функций определяет множество связей из элементов переходов в элементы позиций. Динамическими объектами сетей Петри являются подмодели сети Петри, описывающие процессы системы, выполняемые параллельно, между к-рыми возникают потоки данных и потоки управляющих сигналов. Все потоки возникают при выполнении опред условий, что позволяет их трактовать в качестве причинно-следств связей. Маркированная (размеченная) сеть: Nm=<B,D,I,O,M> M: B®{0,1,2,3,…} Условие срабатывания перехода dj: biÎI(dj) M(bi)³1 Процесс перехода M(bi) ®M’(bi): M’(bi)= M(bi)-I(dj)+O(dj) Отражение временных параметров: временные сети, Е-сети, сети Мерлина. Для придания сети Петри динамических свойств вводится дополнительное множество (мн-во маркеров сети). Каждый элемент маркера показывает кол-во динамич объектов, ассоциируемых с каждым элементом множ-ва позиций. Элемент множества переходов считается готовым к переходу, если: - для него существует не пустое множество значений функции ввода. - связанные с ним элементы позиций (источники динамических объектов) имеют значение маркера, отличного от нуля В процессе перехода происходит: - уменьшение значения маркера связанного с элементом позиции (источником динамических объектов) - увеличение маркера, связанного с элементом позиции (приемником динамических объектов). N-схемы м/б применены при описании событийно-ориентированных моделей.
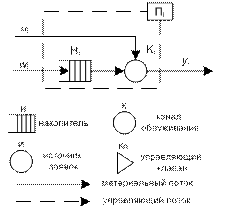
Q-схемы.
w – поток событий прихода заявок (на накопитель Н) u – поток событий обслуживаний (на К) у – выходной поток Системы массового обслуживания (СМО) являются непрерывно-стохастическими системами. При описании СМО м/б использован формализм Q-схем. СМО: - по кол-ву единиц обсл-я (параллельное соед-е приборов): много- и одноканальные - по кол-ву этапов обсл-я(послед. соед. приборов): много- и однофазные - по св-вам каналов(кол-во способов обсл-я): неоднородны и однородные.
Если СМО включает один прибор, то такая СМО является однофазной одноканальной системой. Если СМО включает несколько приборов, соединенных паралл-но к-рые позволяют вести парал-ную обработку нескольких транзактов и в совокупности м/б рассмотрены как одно устр-во, включающее несколько парал-ных каналов обслуживания, то такие системы явл-ся многоканальными. Если несколько приборов соединены послед-но, то транзакты обслуживаются послед-но в каждом приборе (имеют несколько фаз обслуживания), то система является многофазной. Если функционирование канала не меняется на протяжении времени функционирования системы, то система является однородной. Иначе, неоднородная. Поток событий. Однородный поток событий: моменты поступления: 0£t1£t2£…£tn£… интервалы поступлений: t1=t1; t2=t2 -t1;…. Неоднородный поток событий: {ti; fi} Детерминированный поток: t = const Случайный поток событий: t ¹ const Поток с ограниченным последствием: интервалы поступлений независимы. Типы поток событий: - стационарный поток событий (Р не зависти от t); - одинарный поток событий (P(k>1,t, t) ~0); - поток без последствия (P не зависит от n (m не зависит от n)); Простой (пуассоновский) поток: - стационарный - ординарный - без последствий
Поток является стационарным, если он определяется интервалом времени наблюдения и не определяется опред-м моментом времени. Поток событий является ординарным, если в сколько угодно малом промежутке времени возникает только одно событие. Поток наз-ся поток без последствий, если кол-во наблюдаемых событий не одном интервале времени не зависит от кол-ва событий, наблюдаемых на др. интервале времени (интервалы времени не пресекаются) Интенсивность потока событий.
N–число событий за время наблюдения. Интенсивность потока соб-й: l=N/Тн Вероятность появления n событий на интервале [t, t+t]:
Канал обслуживания: - по дисциплине обслуживания: - FIFO - LIFO - по приоритету - по закону распределения - по действию при занятом канале: - отказ - ожидание с ограничением по времени или по длине очереди - ожидание Состояние прибора {кол-во заявок в накопителе, кол-во заявок в очерди}
Параметры Q-схемы:
Системы с потерями: LiН=0 Системы с ожиданием: LiН®¥ Дисциплины обслуживания: - алгоритм выбора из очереди - алгоритм обслуживания
Приоритет заявки: - по процессу захвата канала: - абсолютный - относительный - по процессу формирования - статический - динамический Приоритет транзакта является абсолютным, если транзакт может осуществить прерывание обслуживание др. транзакта. Иначе, относительный. Транзакт с максимальным приоритетом гарантированно первым выбирается из очереди. Приоритет явл-ся статическим, если его значение задается до моделирования и более не меняется. Приоритет динамический, если значения зависят от св-в Q-схемы и в процессе моделирования м/б изменены. Алгоритм функционирования приборов: - правила переполнения канала/накопителя - правила ухода по истечению времени - правила выбора маршрута ухода - правила блокировки каналов
Формализация: Q = <W, U, H, Z, R, A> W – поток событий прихода заявок U – поток событий обслуживания заявок Н – множ-во внутренних параметров системы Z – множ-во состояний системы R – оператор сопряжения приборов A – оператор алгоритмов обслуживания Способы исследования: - аналитические модели - компьютерные модели
А-схемы А-схема (комбинированная) позволяет формализовать системы, включающие непрерывные, дискретные, детерминированные, стохастические компоненты. Нотация А-схем позволяет описать алгоритм функционирования систем. Требования: - адекватное математическое описание - основа для построения алгоритмов - основа для аналитического исследования
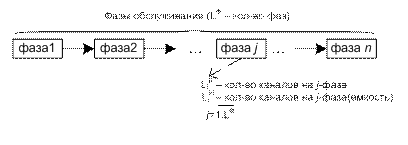
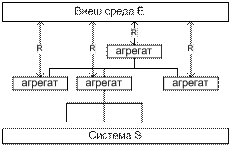
R - оператор сопряжения. Система в терминах А-схем представляет собой совокупность агрегатов(функциональных объектов), характеризуемых вход и выход каналами и алгоритмами функционирования. Вшен среда также представляется по средствам агрегатов. А–схемы поддерживает иерархическое разбиение агрегатов (от общего к частному). Взаимодействие между агрегатами описывается оператором сопряжения R. Оператор R задает взаимооднозначное соответствие между агр.–источником и агр.-приемником сигнала и определяет канал передачи данных и управляющие сигналы.
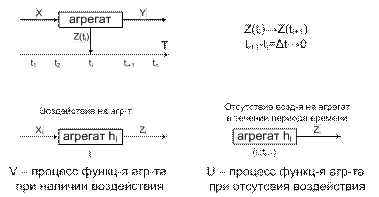
В процессе наблюдения за А-схемой происходит отслеживание состояния всех агр-ов. В общем случае интервал времени между соседними состояния агрегата м/б бесконечно малым. Выделяют 2 режима функционирования агрегата: при наличии и отсутствии внеш воздействий. Состояние в момент времени t0: Z0=Z(t0) Состояние при наличии сигнала в момент tn: Z(tn)=V[t, tn, Z(tn-1),xn] Состояние, если в течение (tn, tn+1) на было сигналов: Z(t)=U[t, tn, Z(tn)] F(V,U) – оператор перехода агр-ов в новые состояния.
V □ - процесс функционирования при регистрации сигнала U ■– проесс функционирования при отсутствии сигнала. Скачек состояния в особый момент времени: Z(tδ)=W[tδ, Z(tδ)] Скачек состояния в момент выдачи вых сигнала: y =G[tδ, Z(tδ)] Z(Y) – подмножество состояний выдачи вых сигнала; Z(tδ) Î Z(Y) А-схема описыавется 2 типами состояний: - состояния, возникающие под воздействием внеш сигнала - состояния, возникающие в процессе функционирования агр-та во внеш среде (состояния особых моментов). Вводятся дополнительные операторы для определения скачка состояний в особый момент W и оператор формирования отклика G. Формализация: A = <T, X, Y, Z, Z(Y), H> Операторы V, U, W, G Взаимодействие: - сигналы - сигнал - конченый набор характеристик - элементарные сигналы передаются мгновенно независимо по элементарным каналам - вход – один элементарный канал - выход – один и более элементарных каналов. Взаимодействие между агрегатами происходит с помощью сигналов. Каждый сигнал описывает-ся конечным набором характеристик. Выделяют элементарные и сложные сигналы. Слож сигналы должны быть дополнительно обработаны. Существует ограничение для вход и выход каналов агрегата.
Определения: случайная величина, вероятностная мера, плотность вероятности, функция распределения. Связь функции распределения с плотностью вероятности (вероятностной мерой).
Случайная величина (СВ) – это функция (или правило), которая определяет вещественное число каждому элементу в пространстве выборки S. Все вероятностные характеристики дискретной СВ Х могут быть вычислены с помощью функции p (x)= P (X = xi), называемой вероятностной мерой дискетной СВ Х. СВ Х считает непрерывной, если существует такая неотрицательная функция f (x), при к-рой для любого множества вещественных чисел В:
Все вероятностные характеристики непрерывной СВ Х могут вычисляться с помощью функции f (x), к-рая называется плотностью распределения вероятностей непрерывной СВ Х. Функция распределения вероятностей (интегральная ф-ция рапред-я вероятностей) F (x) СВ Х определяется для каждого вещественного числа х след образом: F (x)= P (X ≤ x) для -∞< x <∞. Следовательно, F (x) – это вероятность того что, после выполнения эксперимента случайная величина Х получит значение, не превышающие число х. Св-ва ф-ции распред-я: - 0≤ F (x) ≤1 - явл-ся неубывающей функцией -
Плотность распределения вероятностей непрерывной СВ является производной от функции распределения вероятностей: f (x)= F' (x). Функция распределения дискретной СВ: *** P (A) – вероятность наступления события А. Требования к программным моделям. Сущность машинного моделирования системы состоит в проведении на ЭВМ эксперимента с моделью, которая представляет собой некоторый программный комплекс, описывающий формально и (или) алгоритмически поведение элементов системы S в процессе ее функционирования, т. е. в их взаимодействии друг с другом и внешней средой Е. Требованиями пользователя к модели M процесса функцинирования системы S являются: 1. Полнота модели должна предоставлять пользователю возможность получения необходимого набора оценок характеристик системы с требуемой точностью и достоверностью. 2. Гибкость модели должна давать возможность воспроизведения различных ситуаций при варьировании структуры, алгоритмов и параметров системы. 3. Длительность разработки и реализации модели большой системы должна быть по возможности минимальной при учете ограничений на имеющиеся ресурсы. 4. Структура модели должна быть блочной, т. е. допускать возможность замены, добавления и исключения некоторых частей без переделки всей модели. 5. Информационное обеспечение должно предоставлять возможность эффективной работы модели с базой данных систем определенного класса. 6. Программные и технические средства должны обеспечивать эффективную (по быстродействию и памяти) машинную реализацию модели и удобное общение с ней пользователя. 7. Должно быть реализовано проведение целенаправленных (планируемых) машинных экспериментов с моделью системы с использованием аналитико-имитационного подхода при наличии ограниченных вычислительных ресурсов
Требования к проведению машинного эксперимента. Проблемы при проведении машинного эксперимента. Требования к проведению машинного эксперимента: 1. Простота повторений условий эксперимента на ЭВМ с моделью М 2. Возможность управления экспериментом, включая прерывание и возобновление. 3. Легкость управления параметрами воздействия внеш среды. Проблемы при проведении маш-ого эксп-та: 1. Зависимость между последовательностями выходных параметров 2. Определение интервала времени.
Планирование имитационных экспериментов с моделями систем. Основные понятия. Основанная задача планирования машинных экспериментов заключается в получении необходимой информации об исследуемой системе при ограниченных ресурсах (затраты машинного времени, памяти и т.д.) К числу частных задач, решаемых при планировании машинных эксп-ов, относ-ся задачи уменьшения затрат машинного времени на мод-е, уменьшения погрешности результатов мод-я, проверки адекватности модли и т.д. Входные переменные в теории план-я эксп-ов называют факторами, а выходные — реакциями. Стратегическое план-е – ставит своей целью получение необходимой информации о системе S с помощью модели Мм, реализованной на ЭВМ. Цель стр. план-я: 1. Получение функции реакции системы от независимых факторов: y=f(b0,b1,…,bn,x1,x2,…,xk). 2. Нахождение экстремума f(b0,b1,…,bn,x1,x2,…,xk). В качестве результатов планирования используется среднее некотороых распределений, для оценки к-рых применяют выборочные средние, найденные путем многократных прогонов модели ЭВМ. Сходимость выборочных средних с ростом объема выборки называется стохастической. План-е эксп-та представляет собой итерационный процесс, когда выбранная модель плана эксп-та проверяется на реализуемость, а затем, если это необходимо, вносят соответствующие коррективы в модель. Тактическое план-е – определяет способы проведения каждой серии испытания машинной модели Мм. Здесь решаются проблемы: - определения начальных условий и их влияния на достижения установившегося результата при моделировании; - обеспечения точности и достоверности результатов мод-я; - уменьшения дисперсии оценок хар-тик процесса функционирования моделируемых систем; - выбор правил автоматической остановки имитационного эксп-та с моделями.
Архитектура языков моделирования. Требования к языкам имитационного моделирования. Арх-ру ЯИМ, т.е. концепуцию взаимосвязей элементов языка как сложной системы, и технологию перехода от системы S к ее машинной модели М можно представить следующим образом: 1. Объекты мод-я (системы S) описываются (отображаются в языке) с помощью некоторых атрибутов языка; 2. Атрибуты взаимодействуют с процессами, адекватными реально протекающим явл-ям в мод-мой системе S; 3. Процессы требуют конкретных условий, определяющих логическую основу и последовательность взаимодействия этих процессов во времени; 4. условия влияют на события, имеющие место внутри объекта мод-ния и при взимодействии с внеш средой E; 5. События изменяют состояния модели системы М в пространстве и во времени. Типовая схема архитектуры ЯИМ и технология его использования при моделировании систем:
Требования к ЯИМ. § Совмещение. Паралл-но протекающие в реальных системах процессы представляются с помощью последовательно работающей ЭВМ. ЯИМ позволяют обойти эту трудность путём введения понятий системного времени. § Размер. ЯИМ используют динам-ое распределение памяти (компоненты модели системы появляются в ОЗУ и исчезают в зависимости от текущего состояния). Эффект-ть мод-я достигается так же использованием блочных конструкций: блоков, подблоков и т.д. § Изменения. ЯИМ предусматривают обработку списков, отражающих изменения состояний процесса функционирования мод-мой системы на системном уровне. § Взаимосвязь. Для отражения большого количества взаимосвязей между компонентами модели в статике и динамике ЯИМ включаем системно организ-ые логические возможности и реализации теории множ-в. § Стохастичность. ЯИМ используют специальные программные генерации последовательностей случайных числе, программы преобразования в соответствующие законы распределения. § Анализ. ЯИМ предусматривает системные способы статической обработки и анализа результатов моделирования.
GPSS. Косвенная адресация. Пример косвенной адресации. Идея косвенной адресации состоит в том, что каждый транзакт в некотором своем параметре содержит номер того или иного объекта, а в операндах блоков, адресующихся к объектам, записывается ссылка на этот параметр транзакта. При косвенной адресации СЧА определяются как СЧА*параметр. Это означает следующее: - СЧА*j, j – номер параметра активного транзакта (положительное целое число), содержащего номер нужного блока; - СЧА*имя, имя – имя параметра активного транзакта, содержащего номер нужного блока. Например, Q*3 – текущее значение длины очереди, номер которой является значением 3 параметра 3 активного транзакта, SR*Rem – коэффициент использования памяти, номер которой содержится в параметре с именем Rem активного транзакта. Пример: SEIZE P*X1 Занять ОКУ, номер которого содержится в параметре; номер этого параметра определяется значением ячейки Х1. SAVEVALUE 1, X*P2 Поместить в ячейку с номером 1, значение содержащееся в ячейке, номер которой определяется значением параметра 2 транзакта.
Моделирование как метод научного познания. Процессы получения и обработки информации. Формирование и проверка гипотез.
Объект исследования представляет собой некую сущность (элемент, система, компонент и т.д.), о которой необходимо получить сведения(св-ва, характеристики, законы функционирования и т.д.). В общем случае на основании этих сведений формируется шаблон воздействия на объекты с целью достижения определенного эффекта(улучшение характеристик, выявление срытых механизмов функционирования и т.д.).
Изначально исследователь имеет min объем данных об исследуемом объекте. Кроме того, исследователь обладает информацией об окружающей среде данного объекта. На основании этой первичной информации исследователь формирует ряд гипотез относительно того как рассматриваемый объект может взаимодействовать с окружающей средой и к чему это может привести. По сформулированной гипотезе происходит расширение по данным об объекте и организует расширенный эксперимент. На основании экспериментальных данных осуществляется проверка первичных гипотез.
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 439; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.231.116 (0.011 с.) |






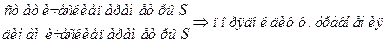
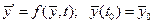
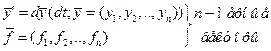
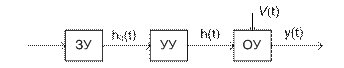
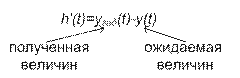

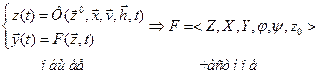


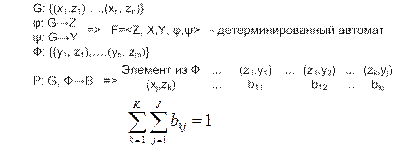
 Сети Петри N =< B, D, I, O >
Сети Петри N =< B, D, I, O >