Прогностическое моделирование (Predictive Modeling)

Здесь, на второй стадии ИАД, используются плоды работы первой, то есть найденные в БД закономерности применяются для предсказания неизвестных значений:

Ø при классификации нового объекта мы можем с известной уверенностью отнести его к определенной группе результатов рассмотрения известных значений его атрибутов;

Ø при прогнозировании динамического процесса результаты определения тренда и периодических колебаний могут быть использованы для вынесения предположений о вероятном развитии некоторого динамического процесса в будущем.

Возвращаясь к рассмотренным примерам, продолжим их на данную стадию. Зная, что некто Иванов - программист, можно быть на 61% уверенным, что его возраст <=30 годам, и на 98% - что он <=60 годам. Аналогично, можно сделать заключение о 84% вероятности того, что некоторое новое юридическое лицо будет находиться в муниципальной собственности, если его основной вид деятельности - "Общеобразовательные детские школы".

Следует отметить, что свободный поиск раскрывает общие закономерности, т. е. индуктивен, тогда как любой прогноз выполняет догадки о значениях конкретных неизвестных величин, следовательно, дедуктивен. Кроме того, результирующие конструкции могут быть как прозрачными, т. е. допускающими разумное толкование (как в примере с произведенными логическими правилами), так и нетрактуемыми - "черными ящиками" (например, про построенную и обученную нейронную сеть никто точно не знает, как именно она работает).

 

Анализ исключений (Forensic Analysis)

Предметом данного анализа являются аномалии в раскрытых закономерностях, то есть необъясненные исключения. Чтобы найти их, следует сначала определить норму (стадия свободного поиска), вслед, за чем выделить ее нарушения. Так, определив, что 84% общеобразовательных школ отнесены к муниципальной форме собственности, можно задаться вопросом - что же входит в 16%, составляющих исключение из этого правила? Возможно, им найдется логическое объяснение, которое также может быть оформлено в виде закономерности. Но может также статься, что мы имеем дело с ошибками в исходных данных, и тогда анализ исключений может использоваться в качестве инструмента очистки сведений в хранилище данных.

 

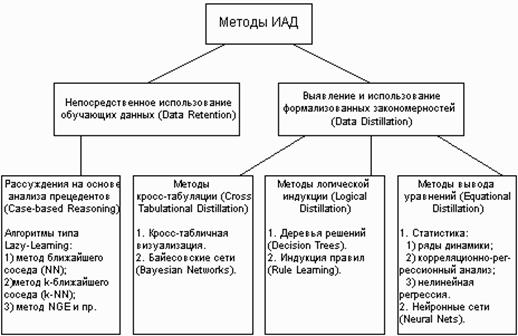
Классификация технологических методов ИАД

Все методы ИАД подразделяются на две большие группы по принципу работы с исходными обучающими данными.

Ø В первом случае исходные данные могут храниться в явном детализированном виде и непосредственно использоваться для прогностического моделирования и/или анализа исключений; это так называемые методы рассуждений на основе анализа прецедентов. Главной проблемой этой группы методов является затрудненность их использования на больших объемах данных, хотя именно при анализе больших хранилищ данных методы ИАД приносят наибольшую пользу.

Ø Во втором случае информация вначале извлекается из первичных данных и преобразуется в некоторые формальные конструкции (их вид зависит от конкретного метода). Согласно предыдущей классификации, этот этап выполняется на стадии свободного поиска, которая у методов первой группы в принципе отсутствует. Таким образом, для прогностического моделирования и анализа исключений используются результаты этой стадии, которые гораздо более компактны, чем сами массивы исходных данных. При этом полученные конструкции могут быть либо "прозрачными" (интерпретируемыми), либо "черными ящиками" (нетрактуемыми).

Две эти группы и входящие в них методы представлены на рис. 7.

 

Рис. 7. Классификация технологических методов ИАД.

 

Логические методы наиболее универсальны. Они что могут работать как с численными, так и с другими типами атрибутов. Построение уравнений требует приведения всех атрибутов к численному виду, тогда как кросс-табуляция, напротив, требует преобразования каждого численного атрибута в дискретное множество интервалов.

Методы кросс-табуляции

Кросс-табуляция является простой формой анализа, широко используемой в генерации отчетов средствами систем оперативной аналитической обработки (OLAP). Двумерная кросс-таблица представляет собой матрицу значений, каждая ячейка которой лежит на пересечении значений атрибутов. Расширение идеи кросс-табличного представления на случай гиперкубической информационной модели является, как уже говорилось, основой многомерного анализа данных, поэтому эта группа методов может рассматриваться как симбиоз многомерного оперативного анализа и интеллектуального анализа данных.

Метод индукции

Индукция правил создает неиерархическое множество условий, которые могут перекрываться. Индукция правил осуществляется путем генерации неполных деревьев решений, а для того чтобы выбрать, какое из них будет применено к входным данным, используются статистические методы. Алгоритмы индукции ассоциативных правил лучше всего подходят для последовательностей и ассоциаций или для задач анализа сходства, таких, как анализ корзины.

 

Одним из способов представления знаний в экспертных системах являются системы правил вида ЕСЛИ (УСЛОВИЕ) ТО (СЛЕДСТВИЕ) С ВЕСОМ (W) В ра­боте представлен индуктивный алгоритм для построения систем правил (ана­логичных используемым в системе Prospector) непосредственно из данных Исход ними данными для работы алгоритма является обучающая выборка D = {(х, у)} состоящая из набора помеченных примеров, где каждый пример х представляет собой вектор значений номинальных признаков Х₁, Х₂,,Х_п, а метка у рассма­тривается как значение номинального классового признака Y Предполагается, что существует (неизвестное) совместное распределение Р признаков Х₁, Х₂,,Х_п, Y. В качестве условия используется конъюнкция элементов типа «признак—значение» X_i = х ∈ Dom(X_i), 1 n, а в качестве следствия указание назначение классового признака Y = у ∈ Dom(Y). Наиболее важными параметрами алгоритма являются максимально допустимая длина конъюнкции левой части правил L и уровень зна­чимости Q критерия, используемого для проверки статистической значимости правил. Выход алгоритма представляет собой набор статистически значимых правил R(D, L, a). Использованием оператора композиции весов для правил с одинаковой правой частью набору правил R(D, L, a)может быть сопоставлен класси­фикатор F_{D, L}, _a: Dom(X₁) * Dom(X₂) * … * Dom(X_n) → Dom(Y). Важной зада­чей при использовании алгоритма является выбор параметров L и a таким образом, чтобы вероятность ошибочной классификации P { F_{D, L}, _a (x)¹ у} с использованием классификатора F_{D, L}, _a была минимальна. В [2] был предложен модифицированный алгоритм, позволяющий осуществлять выбор максимальной длины конъюнкции L на основе метода структурной минимизации эмпирического риска. Нами разработан алгоритм, позволяющий осуществлять одновременную оптимизацию выбора обоих указанных выше параметров Алгоритм основан на вычислении оценок вероятно­стей ошибочкой классификации при различных значениях параметров L и a методом кросс проверки. Используемый в алгоритме способ перебора конъюнкций, составля­ющих условие, позволяет осуществлять интерактивный контроль и автоматический останов процесса вычислений (до достижения наибольшего значения L равного n) по определенным критериям Результаты тестирования алгоритма на базах данных UCI репозитария [3] показывают, что его применение позволяет (при умеренных вы числительных затратах) в определенных ситуациях уменьшить количество правил в R(D, L, a) с одновременным уменьшением вероятности ошибочной классификации.

 

Методы логической индукции

Методы данной группы являются, пожалуй, наиболее выразительными, в большинстве случаев оформляя найденные закономерности в максимально "прозрачном" виде. Кроме того, производимые правила, в общем случае, могут включать как непрерывные, так и дискретные атрибуты. Результатами применения логической индукции могут быть построенные деревья решений или произведенные наборы символьных правил.

Деревья решений являются упрощенной формой индукции логических правил. Основная идея их использования заключается в последовательном разделении обучающего множества на основе значений выбранного атрибута, в результате чего строится дерево, содержащее:

Ø терминальные узлы (узлы ответа), задающие имена классов;

Ø нетерминальные узлы (узлы решения), включающие тест для определенного атрибута с ответвлением к поддереву решений для каждого значения этого атрибута.

В таком виде дерево решений определяет классификационную процедуру естественным образом: любой объект связывается с единственным терминальным узлом. Эта связь начинается с корня, проходит путь по дугам, которым соответствуют значения атрибутов, и доходит до узла ответа с именем класса. Примем допущение, что примеры относятся к двум классам - положительному и отрицательному (в общем случае классов может быть больше).

 

Поскольку исходные данные для индукции часто бывают зашумлены, наилучшим решением с точки зрения прогностической точности является не полное дерево решений, объясняющее все примеры обучающего множества, а упрощенное, в котором некоторые поддеревья свернуты в терминальные узлы. Процесс упрощения, или подрезания (pruning), построенного полного дерева имеет целью избежание переподгонки (overfitting), то есть избыточного усложнения, которое может оказаться следствием излишне буквального следования зашумленным данным.

После подрезания дерева его различные терминальные узлы оказываются на разных уровнях, то есть путь к ним включает разное количество проверок значений атрибутов; другими словами, для прихода в терминальные узлы, лежащие на высоких уровнях дерева, значения многих атрибутов вообще не рассматриваются. Поэтому при построении деревьев решений порядок тестирования атрибутов в узлах решения имеет решающее значение.

Стратегия, применяемая в алгоритмах индукции деревьев решений, называется стратегией разделения и захвата (divide-and-conquer), в противовес стратегии отделения и захвата (separate-and-conquer), на которой построено большое количество алгоритмов индукции правил. Quinlan описал следующий алгоритм разделения и захвата.

 

Пусть:

А - множество атрибутов;

V_i - множество возможных значений атрибута (таким образом, области определения непрерывных атрибутов для построения деревьев решений также должны быть разбиты на конечное множество интервалов).

Тогда:

Ø если все обучающие примеры принадлежат одному классу, то дерево решений есть терминальный узел, содержащий имя этого класса;

Ø в противном случае следует:

а) определить атрибут с наименьшей E-оценкой a_best;

б) для каждого значения v_{best, i} атрибута a_best провести ветвь к поддереву решений, рекурсивно строящемуся на основе примеров со значением v_{best, i} атрибута a_best.

Quinlan предложил вычислять E-оценку следующим образом. Пусть для текущего узла:

 

p - число положительных примеров;

n- число отрицательных примеров;

p_ij- число положительных примеров со значением для;

n_ij- число отрицательных примеров со значением для.

 

Тогда:

где

E-оценка - это теоретико-информационная мера, основанная на энтропии. Она показывает меру неопределенности в классификации, возникающей при использовании рассматриваемого атрибута в узле решения. Поэтому считается, что наибольшую классифицирующую силу имеет атрибут с наименьшей E-оценкой. Однако, определенная рассмотренным образом E-оценка имеет и недостатки: она, в частности, предоставляет при построении дерева преимущество атрибутам с большим количеством значений.

Подрезание дерева решений для улучшения прогностической точности при классификации новых примеров обычно производят над построенным полным деревом, то есть выполняют процедуру поступрощения. Двигаясь снизу-вверх, заменяют узлы решения с соответствующими поддеревьями терминальными узлами до тех пор, пока не будет оптимизирована заданная эвристическая мера.

 

Индукция правил

 

Популярность деревьев решений проистекает из быстроты их построения и легкости использования при классификации. Более того, деревья решений могут быть легко преобразованы в наборы символьных правил - генерацией одного правила из каждого пути от корня к терминальной вершине. Однако, правила в таком наборе будут неперекрывающимися, потому что в дереве решений каждый пример может быть отнесен к одному и только к одному терминальному узлу. Более общим (и более реальным) является случай существования теории, состоящей из набора неиерархических перекрывающихся символьных правил. Значительная часть алгоритмов, выполняющих индукцию таких наборов правил, объединяются стратегией отделения и захвата (separate-and-conquer), или покрывания (covering), начало которой положили работы R. Michalski. Термин "отделение и захват" сформулировали Pagallo и Haussler, охарактеризовав эту стратегию индукции следующим образом:

 

Ø произвести правило, покрывающее часть обучающего множества;

Ø удалить покрытые правилом примеры из обучающего множества (отделение);

Ø последовательно обучиться другим правилам, покрывающим группы оставшихся примеров (захват), пока все примеры не будут объяснены.

Рис. 8 показывает общий алгоритм индукции правил методом отделения и захвата. Разные варианты реализации вызываемых в общем алгоритме подпрограмм определяют разнообразие известных методов отделения и захвата.

 

Рис. 8. Общий алгоритм отделения и захвата для индукции правил.

Алгоритм SEPARATEANDCONQUER начинается с пустой теории. Если в обучающем множестве есть положительные примеры, вызывается подпрограмма FINDBESTRULE для извлечения правила, покрывающего часть положительных примеров. Все покрытые примеры отделяются затем от обучающего множества, произведенное правило включается в теорию, и следующее правило ищется на оставшихся примерах. Правила извлекаются до тех пор, пока не останется положительных примеров или пока не сработает критерий остановки RULESTOPPINGCRITERION. Зачастую полученная теория подвергается постобработке POSTPROCESS.

Процедура FINDBESTRULE ищет в пространстве гипотез правило, которое оптимизирует выбранный критерий качества, описанный в EVALUATERULE. Значение этой эвристической функции, как правило, тем выше, чем больше положительных и меньше отрицательных примеров покрыто правилом-соискателем (candidate rule). FINDBESTRULE обрабатывает Rules, упорядоченный список правил-соискателей, порожденных процедурой INITIALIZERULE.

Новые правила всегда вставляются в нужные места (INSERTSORT), так что Rules постоянно остается списком, упорядоченным по убыванию эвристических оценок правил. В каждом цикле SELECTCANDIDATES отбирает подмножество правил-соискателей, которое затем очищается в REFINERULE. Каждый результат очистки оценивается и вставляется в отсортированный список Rules, если только STOPPINGCRITERION не предотвращает это. Если оценка NewRule лучше, чем у лучшего из ранее найденных правил, значение NewRule присваивается переменной BestRule. FILTERRULES отбирает подмножество упорядоченного списка правил, предназначенное для использования в дальнейших итерациях. Когда все правила-соискатели обработаны, наилучшее правило возвращается.

Основной проблемой, стоящей перед алгоритмами индукции правил, остается избежание переподгонки при использовании зашумленных данных. Средства избежания переподгонки в алгоритмах отделения и захвата могут обрабатывать шум:

Ø на этапе генерирования правил - предупрощение (pre-pruning), реализуемое подпрограммами RULESTOPPINGCRITERION и STOPPINGCRITERION обобщенного алгоритма (их основная идея - остановить генерацию правила или теории, которые еще достаточно общи; таким образом, допускается покрытие ими некоторых отрицательных примеров, если их текущий вид уже считается критерием остановки достаточно ценным); и/или

Ø на стадии постобработки построенной теории - поступрощение (post-pruning), подпрограмма POSTPROCESS общего алгоритма (эти методы заимствуют идею подрезки созданного дерева решений).

Furnkranz классифицирует алгоритмы отделения и захвата по типам производимых концептов.

1. Наборы правил-высказываний (Propositional rule sets). Классические алгоритмы отделения и захвата индуцируют наборы правил на основе троек (атрибут, оператор, значение).

2. Списки решений (Decision lists). Более усложненные алгоритмы обобщают первый подход до индукции упорядоченных наборов правил (называемых списками решений). Такие алгоритмы чаще всего применяются для решения многоклассовых задач, где варианты классификации примеров не ограничиваются определением их положительности или отрицательности.

3. Регрессионные правила (Regression rules). Индукция регрессионных правил позволяет решать задачи с непрерывными классовыми переменными [44]; здесь мы имеем дело с пересечением сфер влияния методов логической индукции и методов вывода уравнений, разделенных на рис. 4 в разных группах.

4. Логические программы (Logic programs). Исследования в области индуктивно-логического программирования породили ряд алгоритмов отделения и захвата, способных решать задачи в терминах более богатого языка логики предикатов первого порядка. На выходе таких алгоритмов могут быть получены программы на Прологе.

Стратегия отделения и захвата не является единственным способом индукции символьных правил. Например, Quinlan предложил алгоритм индукции деревьев решений, который позволяет генерировать компактные списки решений из деревьев решений посредством перевода деревьев решений во множество неперекрывающихся правил, упрощения этих правил и упорядочивания полученных перекрывающихся правил в список решений. В качестве средства генерации правил могут применяться и генетические алгоритмы, воплощающие идею мутаций и отбора лучших правил.