
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цель и задачи математических методов в географии.Содержание книги
Поиск на нашем сайте
Вопросы по математическим методам в географии 1. Цель и задачи математических методов в географии. 2. Ранговая корреляция. 3. Генеральная и выборочная совокупность. 4. Регрессионный анализ, виды регрессий. 5. Определение объема выборочной совокупности. 6. Способы составления уравнения регрессии. 7. Правила составления репрезентативных выборок. 8. Моделирование линейного уравнения регрессии. 9. Артефакт и его использование. 10. Моделирование нелинейного уравнения параболической зависимости. 11. Ошибки выборочных критериев. 12. Моделирование нелинейного уравнения гиперболической зависимости. 13. Степень свободы и ее использование. 14. Факторный анализ и его использование. 15. Определение точности опыта, использование показателя. 16. Этапы факторного анализа. 17. Графическое представление вариационного ряда. Деление выборки на классы. 18. Интерпретация результатов факторного анализа. 19. Показатели ассиметрии и эксцесса. 20. Области применения линейного программирования. 21. Теоретические распределения. 22. Виды транспортных задач. 23. Показатели среднего положения. 24. Способы составления базисного допустимого плана. 25. Показатели разнообразия выборки. 26. Правила составления цепи в матрице. 27. Независимые и сопряженные выборочные совокупности. 28. Решение транспортных задач методом функционала. 29. Использование и расчет критерия Стьюдента. 30. Решение транспортных задач методом потенциала. 31. Использование и расчет наименьшей существенной разницы (НСР). 32. Открытые и закрытые транспортные задачи. 33. Использование и расчет критерия Фишера. 34. Решение транспортных задач дельта – методом 35. Использование и расчет критерия Пирсона. 36. Многоэтапная транспортная задача. 37. Использование дисперсионного анализа. 38. Многопродуктовая транспортная задача. 39. Составление дисперсионного комплекса. 40. Сетевое решение транспортных закрытых задач. 41. Сетевое решение открытых транспортных задач. 42. Информационный анализ и его применение. 43. Меры теории графов, их назначение. 44. Использование информационного анализа в картографии. 45. Основные элементы теории графов. 46. Кластерный анализ и условия его применения. 47. Классификация на основе теории графов. 48. Этапы вычислений в кластерном анализе. 49. Географическое поле и его использование. 50. Правила построения дендрограммы в кластерном анализе. 51. Корреляционный анализ и его использование. 52. Виды связей между явлениями, объектами. 53. Условия для расчета коэффициента корреляции. 54. Моделирование в географии. 55. Условия для расчета корреляционного отношения. 56. Виды моделей и отбор информации. 57. Тренд-анализ. 58. Моделирование уравнения множественной регрессии.
Цель и задачи математических методов в географии. Географические исследования и практические задачи базируются на большом объеме количественной информации, которую необходимо объективно оценить и провести группировку или классификацию, доказать зависимость или провести моделирование, выявить оптимальные условия развития или установить пространственные закономерности развития объектов или явлений, дать прогноз их развития. Эти вопросы успешно решаются с помощью математических методов и соответствующих программ, разработанных для ПЭВМ. Исследователь или практик должен лишь четко сформулировать задачу, выбрать наиболее подходящий для конкретных условий математический метод анализа и дать объективную интерпретацию результатов. Математика позволяет нам решать задачи частные и общие. Например, расход воды в реке рассчитывается на основе специальной частной формулы, а загрязнение воды в реке под воздействием предприятия оценивается с применением факторного анализа – общего для решения многих специальных географических задач. Современные географические методы исследования сравнительно-географический, системный и другие необходимо использовать в сочетании с математическим обоснованием результатов. Математические методы позволяют широко использовать системный анализ, как наиболее совершенный. Любой географический объект исследования может быть представлен как система – определенный объект, состоящий из множества частей, которые взаимосвязаны не только между собой, но и с соседними объектами-системами. Установить целостность и структуру, иерархичность, величину и направленность связей в системе, их характер позволяют математические методы путем создания формализованных систем. Системный подход основан на исследовании объектов как систем, создает единую теоретическую модель. Системный анализ представляет собой совокупность методологических средств, позволяющих обосновать проблемы научно-практического характера. Успешное использование системного анализа возможно при реализации следующих важнейших принципов, опирающихся на математические методы:выявляется и формулируется конечная цель исследования; система-объект рассматривается как единое целое, в ней выявляются все взаимосвязи и их результаты; строится обобщенная комбинированная модель (модели), где отображаются структура, иерархия и взаимосвязи. Выделяются две группы систем: материальные и абстрактные. Традиционные методы географии изучают материальные системы. Социальные системы через техногенез могут оказывать воздействие на природные. По развитию выделяют системы статичные (предприятия) и динамичные (ландшафт). По характеру взаимодействия системы делятся на закрытые (в них не поступает и из них не выводится вещество, происходит лишь обмен энергией) и открытые (постоянно происходит ввод и вывод вещества и обмен энергией). В открытой системе, например, ландшафте постоянно протекающие процессы и явления создают подвижное равновесие, т.е. некоторую стабильность в определенных условиях среды и общества. Среди абстрактных систем на основе различных систематизирующих отношений можно выделить: функциональные (математическая модель), структурные (глобус), временные (прогноз погоды), геометрические (линия регрессии на графике). В научную литературу введено понятие управляющая система, которая рассматривается как схематическое отображение реальных объектов. Она задается элементами, схемой и координатами. Элементы определяются через их свойства. Схема показывает характер соединений между элементами. Координаты показывают относительное положение выделенных элементов управляющей системы. Любая управляющая система не мыслится без понятия функции – отображения одного множества в другом как действие с реальными предметами или как вещественный процесс (например, функция растительности – создание органического вещества из неорганического с использованием солнечной энергии в процессе фотосинтеза).
Ранговая корреляция. В географических исследованиях иногда приходится обрабатывать быстро и с наименьшими затратами фактический материал, даже если получаются менее точные результаты. В некоторых случаях работают с качественной информацией или с громоздкими вычислениями. В таких случаях для установления зависимости между признаками используется ранговая корреляция. Процесс упорядочения вариант по какому-либо признаку (например, увеличение или уменьшение количества населения по районам) называют ранжированием. Каждому члену ранжированного ряда присваивается ранг. Для обозначения рангов, как правило, используются числа в пределах единиц и десятков, например: 1, 2, 3,..., n. Ранговую корреляцию можно применять для всех упорядоченных признаков (например, экспертные оценки, баллы, бонитеты). Объем сопряженных выборок должен быть не менее пяти. Коэффициент ранговой корреляции характеризуется следующими свойствами. 1. Если ранжированные варианты выборочных совокупностей имеют один и тот же ранг независимо от цели ранжирования, то коэффициент корреляции должен быть равен +1, т. е. существует полная положительная функциональная зависимость. 2. Если ранги вариант в сравниваемых рядах выборочных совокупностей расположены в обратной последовательности, то коэффициент корреляции равен –1, т. е. будет иметь место полная обратная функциональная зависимость. 3. В других случаях коэффициент ранговой корреляции имеет значения между +1 и –1, что больше соответствует фактической связи между признаками. Для расчета зависимости (х, у)существуют следующие коэффициенты ранговой корреляции: коэффициент неупорядоченности r н и коэффициент Спирмена r с. Коэффициент ранговой корреляции Спирмена рассчитать легче, чем коэффициент неупорядоченности, поэтому в естественных науках предпочтение отдается r с. Коэффициент Спирмена представляет собой следующее соотношение:
где d – разность между сопряженными рангами; х' – величины рангов, заменяющие фактические варианты или качественные признаки по аргументу х; у' – величины рангов, заменяющие фактические варианты или качественные признаки по функции у; N п – количество сопряженных пар. Достоверность полученного рангового коэффициента можно установить аналогично достоверности коэффициента корреляции. Линейная зависимость Линейная регрессия на графике изображается в виде прямой так, чтобы точки эмпирической линии располагались по обе стороны ее и по возможности ближе к ней. Известно следующее уравнение линейной регрессии: y = ax + b (6.1) где у – значение зависимой переменной (признак); х – значение независимой переменной (фактор, влияющий на признак); а – коэффициент регрессии, показывающий степень зависимости между переменными (может быть также выражен тангенсом угла наклона линии регрессии к оси абсцисс); b – ордината линии, показывающая смещение начала прямой относительно начала координат. Гиперболическая зависимость При проведении исследований может быть установлена нелинейная зависимость между аргументом и функцией, представляющая собой на графике кривую в виде гиперболы. Общее уравнение регрессии для гиперболической зависимости имеет вид y = a/x + b (6.5) где х – аргумент; у – функция; а и b – коэффициенты, величину которых следует установить. Расчет сводится к следующему. Чтобы установить вид зависимости между функцией и аргументом, по исходным данным строится график. Затем при вычислении параметров а и b по способу координат точек подбираются две точки, расположенные на кривой или около нее по методу, описанному для линейной регрессии. Параболическая зависимость Общее уравнение параболы n -го порядка имеет вид y = axn + bxn– 1 + cxn– 2 + … + kx + l. Если ограничиться второй ступенью независимой переменной величины х,будем иметь частный случай параболы второго порядка: y = ax 2 + bx + c Множественная регрессия Если при установлении зависимости между признаками используется больше одной независимой переменной, то применяют множественный регрессионный анализ. Проведение такого анализа возможно в следующих условиях: распределение зависимой переменной при различных значениях независимых должно быть близко к нормальному; дисперсия зависимой переменной при разных значениях признаков х должна считаться одинаковой. С увеличением числа признаков и в случаях нелинейной множественной регрессии необходимо использовать ЭВМ. Поэтому рассмотрим простой вариант множественной линейной регрессии без применения ЭВМ, когда один признак зависит от двух факторов. Общее уравнение линейной множественной регрессии имеет вид y = a + bx + cz (6.9) Для вычисления параметров а, b, с составляется система уравнений. Этапы факторного анализа. Первый этап. Производится вычисление коэффициентов корреляции между всеми изучаемыми параметрами. Второй этап. Для описания параметров используется линейная модель (параметры выражаются через скрытые гипотетические факторы линейно). Основная модель факторного анализа может быть записана в виде формулы: zj=a_j1 F_1+a_j2 F_2+⋯+a_jm F_m+d_j u_ji где zj – параметр, F1 – фактор; aji – приближение (коэффициент) факторного отображения (нагрузки). Первый член правой части равенства показывает долю первого фактора в исследуемых явлениях, второй – долю второго фактора, последний – долю независимого фактора (остаток). Чем больше величина коэффициента факторного отображения при факторе, тем больше роль данного фактора в рассматриваемом явлении. Третий этап. Проводим группировку параметров с целью определения факторов. Четвертый этап. Находим первое приближение факторного отображения. Предполагается, что полученные факторы не коррелируют между собой. Для каждой строки матрицы R^x вычисляем сумму коэффициентов корреляции. Пятый этап. Возводим редуцированную матрицу в квадрат. Для этого необходимо каждое число возвести в квадрат в первом столбце матрицы и суммировать результаты. Шестой этап. Вычисляем коэффициенты при первом факторе F1. Седьмой этап. Проводим поиск фактора, который учитывал бы максимум остаточной общности. Для этого после учета F1 необходимо построить матрицу R1 используя коэффициенты первого фактора. Теоретические распределения В статистике используются различные виды теоретических распределений: нормальное распределение, биноминальное распределение, распределение Пуассона и др. Каждое из теоретических распределений имеет специфику и свою область применения в различных отраслях знаний. Чаще всего в качестве теоретического распределения используется нормальное распределение или закон К. Гаусса-А. Лапласа. Нормальное распределение признака наблюдается в тех случаях, когда на величину вариантов, входящих в состав вариационного ряда, действует множество случайных, независимых или слабо зависимых факторов, каждый из которых играет в общей сумме незначительную роль. Нарушение нормального характера распределения часто является свидетельством неоднородности совокупности. Нормальное распределение определяется двумя параметрами: средней арифметической () и средним квадратическим отклонением (). Подчиненность закону нормального распределения проявляется тем точнее, чем больше случайных величин действуют вместе. Если ни одна из случайно действующих причин по своему действию не окажется преобладающей над другими, то закон распределения очень близко подходит к нормальному. В условиях нормального распределения существует следующая зависимость между величиной среднего квадратического отклонения и количеством наблюдений: в промежутке между при t=+1 и t= -1 заключается 68,26% всех значений признаков; между при t=+2 и t= -2 располагается 95,44% всех значений признаков; между при t=+3 и t= -3 находится 99,73% значений признаков. На рис. 8.5 показано нормальное распределение с одно-, двух-, трехсигмовыми пределами. На практике почти не встречаются отклонения, которые превышают. Отклонение может считаться максимально возможным. Это положение называют “правилом трех сигм”. В математической статистике нормальное распределение играет роль некоторого стандарта, с которым сравнивают другие распределения. Виды транспортных задач Транспортные задачи могут быть открытыми, учитывать время транспортировки родукции, затраты на производство единицы продук-ции, многоэтапными, многопродуктовыми. Все они, как и закрытая транспортная задача, являются частным случаем более сложной ямбда-задачи. Ограничения в транспортную задачу вводят при учете времени транспортировки дукции. Для этого в искомом оптимальном плане не должны быть такие перевозки между поставщиками и потребителями, временная продолжительность которых больше заданной величины. В географических исследованиях должны учитываться не только транспортные, но и производственные затраты. Такие задачи получили название транспортно-производственных. В качестве cij = Si + tij высту-пают транспортно-производственные затраты, т. е. Si – затраты на произ-водство единицы продукции (себестоимость, цена единицы продукции или приведенные удельные затраты) i-м поставщиком; tij – затраты на перевозку продукции между i-м поставщиком и j-м потребителем. Если увеличить или уменьшить на одну и ту же величину все показатели cijв матрице или в строке, или в столбце, то свойства матрицы не изменят-ся. Суммарные мощности поставщиков равны суммарному спросу по-требителей. Следовательно, какой бы ни была стоимость производства, потребители для удовлетворения своего спроса возьмут продукцию у всех поставщиков. От каких поставщиков получит каждый потребитель продукцию, зависит от транспортных затрат. Решение открытой транспортно-производственной задачи должно учи-тывать показатель Si, например себестоимость продукции. При суммар-ной мощности поставщиков, предположим, на 20 единиц превышающих суммарный спрос потребителей, у последних появляется свобода выбора в получении продукции от более выгодных поставщиков, поэтому опти-мальный план может быть экономически более эффективным. Дельта-метод Аганбегяна Для решения закрытых и открытых транспортных задач А. Г. Аганбегян (1961) разработал дельта-метод для ручной обработки. Отличие построения цепей в дельта-методе: • цепь строится незамкнутая; • цепь начинается в клетке с кружком (с поставкой), которая находится в минусовой строке; в этой клетке поставка уменьшается и она становится отрицательной вершиной цепи; • перемещение поставки в конец открытой цепи производится как в методе потенциалов с чередованием положительных и отрицательных вершин; • в этом методе не требуется количества кружков (клеток с поставка-ми), равного m + n – 1; • в исходном плане число кружков равно числу столбцов и лишь в ходе решения появляются новые клетки с кружками (поставками); • в незамкнутой цепи вершинами бывают клетки без кружков (без поставок); они положительны, так как в них вносится поставка; • характеристика незамкнутой цепи рассчитывается как алгебраиче-ская сумма показателей ∆Сij или в ее вершинах; так как при распре-делении поставок по цепи функционал увеличивается, характеристика цепи всегда положительная; она показывает, насколько увеличивается в функционал, если передвинуть по цепи поставку, равную 1, из минусовой строки в плюсовую.
35. Критерий Пирсона (хи-квадрат, χ2). Для оценки соответствия или расхождения полученных эмпирических данных и теоретических (рас-четных, прогнозных) распределений применяются статистические кри-терии согласия. Среди них наибольшее распространение получил непараметрический критерий К. Пирсона – хи-квадрат. Его можно использовать с различными формами распределения совокупностей. Как и любой другой статистический критерий, он не доказывает справедливость нулевой гипотезы, а лишь устанавливает с определенной вероятностью ее согласие или несогласие с экспериментальными данными. Критерий применяется при условии наличия не менее 5 наблюдений или частот в каждой группе, классе или совокупности. Малые частоты объединяют. Вычисление проводят по формуле: χ2 = ∑ [(φ – φ΄)2 / ∑ φ΄], (1.26) где φ, φ΄– наблюдения или частоты в опыте соответственно эмпириче-ски или теоретически ожидаемые. Значения χ2 могут быть только положительными и возрастать от нуля до бесконечности. Если вычисленный критерий хи-квадрат больше табличного (теоретического) значения, нулевая гипотеза, которая предполагает соответствие эмпирического и теоретического распределений, отвергается, при χ2выч < χ2табл нулевая гипотеза принимается. Достоверность различий можно определить по правилу Романовского: нулевая гипотеза отвергается, если соблюдается неравенство: D = (χ2 – ν) / >3 Степень свободы при проверке гипотезы о нормальном распределе-нии вычисляется по формуле ν = k – 3, где k – число классов. Различие между экспериментальными вариантами и теоретическими считаются достоверными, если D > 3. Критерий Пирсона тем меньше, чем меньше различаются эмпирические и теоретические частоты. Он не позволяет обнаружить различия, которые скрадывает группировка (объединение малых частот в одну группу). Его удобно использовать, так как не требуется вычислений средних дисперсий. 39. 40. Сетевая задача: Оптимальное планирование перевозок может быть произведено непосредственно на схеме сети путей сообщения Схема состоит из (или дуг) и узлов (или вершин). Вершинами являются пункты или (центры агрегации) погрузки и выгрузки а также все реальные узловые пункты сети. Вершины без погрузки и выгрузки данного груза являются транзитными. Каждый участок (звено) сети между двумя соседними вершинами обычно рассматривают как две дуги противоположного направления с движением в одну сторону по каждой дуге. Сетевая и матричная модели в большинстве случаев взаимозаменяемы. Но есть и особые ситуации, так, например, при большом числе потребителей и поставщиков преимущество имеет сетевая постановка задачи; эта же форма применяется при оптимизации перевозок с учетом ограничений пропускной способности участков транспортной сети.
Тренд-анализ. Используют динамические ряды (тренд-анализ). Они представляют собой однородные статистические величины, показывающие изменение явления или процесса во времени. С помощью тренд-анализа характеризуются тенденции изменения явления во времени, подбираются статистические модели, описывающие эти изменения, производится поиск промежуточных значений путем интерполяции, предсказание результатов значений в перспективе (экстраполяция). Динамические ряды бывают простые (описание одного явления), сложные (описание нескольких явлений), производные (составленные из средних или относительных величин), моментные (оценка события за определенный момент времени), интервальные (анализ явления за год, полгода, месяц). Для создания линии тренда по данным диаграммы применяются регрессионный анализ, описывающий взаимодействие между переменными. Следует лишь выбрать один из шести способов аппроксимации данных: линейная, логарифмическая, полиномиальная, степенная, экспоненциальная, скользящая средняя.
Вопросы по математическим методам в географии 1. Цель и задачи математических методов в географии. 2. Ранговая корреляция. 3. Генеральная и выборочная совокупность. 4. Регрессионный анализ, виды регрессий. 5. Определение объема выборочной совокупности. 6. Способы составления уравнения регрессии. 7. Правила составления репрезентативных выборок. 8. Моделирование линейного уравнения регрессии. 9. Артефакт и его использование. 10. Моделирование нелинейного уравнения параболической зависимости. 11. Ошибки выборочных критериев. 12. Моделирование нелинейного уравнения гиперболической зависимости. 13. Степень свободы и ее использование. 14. Факторный анализ и его использование. 15. Определение точности опыта, использование показателя. 16. Этапы факторного анализа. 17. Графическое представление вариационного ряда. Деление выборки на классы. 18. Интерпретация результатов факторного анализа. 19. Показатели ассиметрии и эксцесса. 20. Области применения линейного программирования. 21. Теоретические распределения. 22. Виды транспортных задач. 23. Показатели среднего положения. 24. Способы составления базисного допустимого плана. 25. Показатели разнообразия выборки. 26. Правила составления цепи в матрице. 27. Независимые и сопряженные выборочные совокупности. 28. Решение транспортных задач методом функционала. 29. Использование и расчет критерия Стьюдента. 30. Решение транспортных задач методом потенциала. 31. Использование и расчет наименьшей существенной разницы (НСР). 32. Открытые и закрытые транспортные задачи. 33. Использование и расчет критерия Фишера. 34. Решение транспортных задач дельта – методом 35. Использование и расчет критерия Пирсона. 36. Многоэтапная транспортная задача. 37. Использование дисперсионного анализа. 38. Многопродуктовая транспортная задача. 39. Составление дисперсионного комплекса. 40. Сетевое решение транспортных закрытых задач. 41. Сетевое решение открытых транспортных задач. 42. Информационный анализ и его применение. 43. Меры теории графов, их назначение. 44. Использование информационного анализа в картографии. 45. Основные элементы теории графов. 46. Кластерный анализ и условия его применения. 47. Классификация на основе теории графов. 48. Этапы вычислений в кластерном анализе. 49. Географическое поле и его использование. 50. Правила построения дендрограммы в кластерном анализе. 51. Корреляционный анализ и его использование. 52. Виды связей между явлениями, объектами. 53. Условия для расчета коэффициента корреляции. 54. Моделирование в географии. 55. Условия для расчета корреляционного отношения. 56. Виды моделей и отбор информации. 57. Тренд-анализ. 58. Моделирование уравнения множественной регрессии.
Цель и задачи математических методов в географии. Географические исследования и практические задачи базируются на большом объеме количественной информации, которую необходимо объективно оценить и провести группировку или классификацию, доказать зависимость или провести моделирование, выявить оптимальные условия развития или установить пространственные закономерности развития объектов или явлений, дать прогноз их развития. Эти вопросы успешно решаются с помощью математических методов и соответствующих программ, разработанных для ПЭВМ. Исследователь или практик должен лишь четко сформулировать задачу, выбрать наиболее подходящий для конкретных условий математический метод анализа и дать объективную интерпретацию результатов. Математика позволяет нам решать задачи частные и общие. Например, расход воды в реке рассчитывается на основе специальной частной формулы, а загрязнение воды в реке под воздействием предприятия оценивается с применением факторного анализа – общего для решения многих специальных географических задач. Современные географические методы исследования сравнительно-географический, системный и другие необходимо использовать в сочетании с математическим обоснованием результатов. Математические методы позволяют широко использовать системный анализ, как наиболее совершенный. Любой географический объект исследования может быть представлен как система – определенный объект, состоящий из множества частей, которые взаимосвязаны не только между собой, но и с соседними объектами-системами. Установить целостность и структуру, иерархичность, величину и направленность связей в системе, их характер позволяют математические методы путем создания формализованных систем. Системный подход основан на исследовании объектов как систем, создает единую теоретическую модель. Системный анализ представляет собой совокупность методологических средств, позволяющих обосновать проблемы научно-практического характера. Успешное использование системного анализа возможно при реализации следующих важнейших принципов, опирающихся на математические методы:выявляется и формулируется конечная цель исследования; система-объект рассматривается как единое целое, в ней выявляются все взаимосвязи и их результаты; строится обобщенная комбинированная модель (модели), где отображаются структура, иерархия и взаимосвязи. Выделяются две группы систем: материальные и абстрактные. Традиционные методы географии изучают материальные системы. Социальные системы через техногенез могут оказывать воздействие на природные. По развитию выделяют системы статичные (предприятия) и динамичные (ландшафт). По характеру взаимодействия системы делятся на закрытые (в них не поступает и из них не выводится вещество, происходит лишь обмен энергией) и открытые (постоянно происходит ввод и вывод вещества и обмен энергией). В открытой системе, например, ландшафте постоянно протекающие процессы и явления создают подвижное равновесие, т.е. некоторую стабильность в определенных условиях среды и общества. Среди абстрактных систем на основе различных систематизирующих отношений можно выделить: функциональные (математическая модель), структурные (глобус), временные (прогноз погоды), геометрические (линия регрессии на графике). В научную литературу введено понятие управляющая система, которая рассматривается как схематическое отображение реальных объектов. Она задается элементами, схемой и координатами. Элементы определяются через их свойства. Схема показывает характер соединений между элементами. Координаты показывают относительное положение выделенных элементов управляющей системы. Любая управляющая система не мыслится без понятия функции – отображения одного множества в другом как действие с реальными предметами или как вещественный процесс (например, функция растительности – создание органического вещества из неорганического с использованием солнечной энергии в процессе фотосинтеза).
Ранговая корреляция. В географических исследованиях иногда приходится обрабатывать быстро и с наименьшими затратами фактический материал, даже если получаются менее точные результаты. В некоторых случаях работают с качественной информацией или с громоздкими вычислениями. В таких случаях для установления зависимости между признаками используется ранговая корреляция. Процесс упорядочения вариант по какому-либо признаку (например, увеличение или уменьшение количества населения по районам) называют ранжированием. Каждому члену ранжированного ряда присваивается ранг. Для обозначения рангов, как правило, используются числа в пределах единиц и десятков, например: 1, 2, 3,..., n. Ранговую корреляцию можно применять для всех упорядоченных признаков (например, экспертные оценки, баллы, бонитеты). Объем сопряженных выборок должен быть не менее пяти. Коэффициент ранговой корреляции характеризуется следующими свойствами. 1. Если ранжированные варианты выборочных совокупностей имеют один и тот же ранг независимо от цели ранжирования, то коэффициент корреляции должен быть равен +1, т. е. существует полная положительная функциональная зависимость. 2. Если ранги вариант в сравниваемых рядах выборочных совокупностей расположены в обратной последовательности, то коэффициент корреляции равен –1, т. е. будет иметь место полная обратная функциональная зависимость. 3. В других случаях коэффициент ранговой корреляции имеет значения между +1 и –1, что больше соответствует фактической связи между признаками. Для расчета зависимости (х, у)существуют следующие коэффициенты ранговой корреляции: коэффициент неупорядоченности r н и коэффициент Спирмена r с. Коэффициент ранговой корреляции Спирмена рассчитать легче, чем коэффициент неупорядоченности, поэтому в естественных науках предпочтение отдается r с. Коэффициент Спирмена представляет собой следующее соотношение:
где d – разность между сопряженными рангами; х' – величины рангов, заменяющие фактические варианты или качественные признаки по аргументу х; у' – величины рангов, заменяющие фактические варианты или качественные признаки по функции у; N п – количество сопряженных пар. Достоверность полученного рангового коэффициента можно установить аналогично достоверности коэффициента корреляции.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 509; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.016 с.) |

 , или
, или 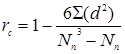 , (5.16)
, (5.16)


