
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы линейных неоднородных уравнений (СЛНУ)Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим систему неоднородных уравнений
Пусть Пусть Вычитая из (7.4) выражение (7.5), получим:
Согласно (7.3) В нашем случае Таким образом:
Теорема 7.2 Общее решение представляется в виде суммы произвольного частного решения этой системы и общего решения соответствующей ей однородной системы. Следствие 1 Разность двух произвольных решений систем линейных неоднородных уравнений является решением соответствующей системы линейных однородных уравнений. Следствие 2 Сумма любого частного решения системы линейных неоднородных уравнений с любым частным решением соответствующей системы линейных однородных уравнений дает частное решение системы линейных неоднородных уравнений. Замечание 2. В формуле (5.5) Пример 7.2
Матричные уравнения 1. Рассмотрим матричное уравнение
где A — квадратная невырожденная (det A ≠ 0) матрица порядка n, B — матрица размера n × m и X — неизвестная матрица. Так как матрица A — невырожденная, то существует обратная матрица A−1. Умножим обе части уравнения слева (операция умножения матриц некоммутативна!) на матрицуA−1. По определению обратной матрицы, получим
Таким образом, искомое решение матричного уравнения определяется формулой
Обратите внимание на то, что количество строк матрицы B должно быть равно порядку матрицы A. 2. Рассмотрим матричное уравнение
где A — квадратная невырожденная (det A ≠ 0) матрица порядка n, B — матрица размера m × n и X — неизвестная матрица. Так как матрица A — невырожденная, то существует обратная матрица A−1. Умножим обе части уравнения справа на матрицу A−1. По определению обратной матрицы, получим
Таким образом, искомое решение матричного уравнения:
Обратите внимание на то, что количество столбцов матрицы B должно быть равно порядку матрицы A. Решить матричное уравнение.
Записываем в матричном виде AX=B Равенство AX=B обычно называют матричным уравнением, и если матрица А невырожденная, то можно найти решение уравнения AX=B с помощью обратной матрицы А -1
Пусть |А| откуда A -1 (AX) = (A -1 A) X = EX = А-1 B или X = А -1 B. Последнее равенство даёт нам все решения матричного уравнения Для А -1 det |А| = 4 (11) + 3 (4) + 18 (-3) = 44 + 12 - 54 = 56 - 54 = 2 Вычислим алгебраические дополнения элементов матрицы А: A11 = 11 A12 = -4 A13 = -3 A21 = -3 A22 = 2 A23 = 1 A31 = -36 A32 = 12 A33 = 10
x1 = 3, x2 = -1, x3 = 1, x4 = 7, x5 = 2, x6 = -1 -17-
-18-
-19- ------ -20- Векторы. Линейные операции над векторами. Проекция вектора на ось. Декартовы координаты векторов и точек.Скалярное произведение векторов, его основные свойства, координатное выражение.
Обозначения: a, ¯a, ¯AB. Определение 5.2. Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Вектор называется нулевым, если его начальная и конечная точки совпадают. Нулевой вектор не имеет определенного направления. Определение 5.3. Два вектора называются равными,если они коллинеарны, имеют одинаковую длину (модуль) и одинаковое направление. Замечание.Таким образом, мы изучаем так называемые свободные векторы, начальная точка которых может быть выбрана произвольно. Векторы, для которых важна точка приложения, называются присоединенными (связанными) и используются в некоторых разделах физики.
Суммой
Наряду с правилом треугольника часто пользуются (равносильным ему) правилом параллелограма: если векторы
Сложение многих векторов производится при помощи последовательного применения правила треугольника (см. рис. 3, где изображено построение суммы четырех векторов
Разность
Произведение Сложение векторов и умножение вектора на число называются линейными операциями над векторами. Имеют место следующие две основные теоремы о проекциях векторов: 1). Проекция суммы векторов на какую-нибудь ось равна сумме ее проекций на эту же ось:
2). При умножении вектора на число его проекция умножается на то же число:
В частности, если
то
и
Если
Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными. Признаком коллинеарности двух векторов
является пропорциональность их координат:
Тройка векторов 1). Вектор 2). Каждый из векторов 3). Векторы Каким бы ни был вектор
коэффициенты этого разложения являются координатами вектора
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1622; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.135.39 (0.01 с.) |

 (7.4)
(7.4) .
. – решение этой системы, т.е.
– решение этой системы, т.е.  (7.5)
(7.5) .
.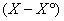 является решением соответствующего однородного уравнения.
является решением соответствующего однородного уравнения. .
. или
или  (7.4).
(7.4). - частное решение системы.
- частное решение системы.

 ,
, 

 0. Умножая обе части AX=B на А -1 слева, получим А -1 (AX) = А -1 B,
0. Умножая обе части AX=B на А -1 слева, получим А -1 (AX) = А -1 B,











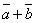 двух векторов
двух векторов 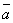 и
и  называется вектор, который идет из начала вектора
называется вектор, который идет из начала вектора 
 .
.
 ,
,  ).
).
 двух векторов
двух векторов 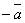 . Легко видеть, что
. Легко видеть, что  . Таким образом, построение разности равносильно прибавлению к «уменьшаемому» вектора, обратного «вычитаемого».
. Таким образом, построение разности равносильно прибавлению к «уменьшаемому» вектора, обратного «вычитаемого». (или также
(или также  ) вектора
) вектора 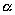 называется вектор, модуль которого равен произведению модуля вектора
называется вектор, модуль которого равен произведению модуля вектора 
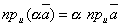 .
. ,
, 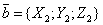 ,
, ,
, .
. , то для любого числа
, то для любого числа  .
.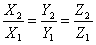 .
. ,
,  ,
,  называется координатным базисом, если эти векторы удовлетворяют следующим условиям:
называется координатным базисом, если эти векторы удовлетворяют следующим условиям: ,
,  ,
,  .
. ;
;


