
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение линейной системыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте В настоящей разработке основным объектом исследования является линейная стационарная система, которая описывается системой линейных дифференциальных уравнений следующего вида:
В этих уравнениях Матрицы Соотношение Многие вопросы теории управления, связанные с изучением математического объекта, заданного соотношениями (1.1), не имеют аналогов в теории обыкновенных дифференциальных уравнений. Однако, прежде чем изучать математические свойства этого объекта, необходимо ввести терминологию и соответствующие понятия, которые устанавливали бы связь этой математической модели и реальных систем управления. Множество значений вектора Вектор Через Пространство пар Введем множество мгновенных значений управляющих воздействий Говорят, что входное воздействие С учетом введенных понятий можно дать определение изучаемого математического объекта. Определение. Линейной системой с непрерывным временем называется система, описываемая соотношениями (1.1), где Таким образом, термином линейная система обозначается линейная, конечномерная, динамическая система с непрерывным временем. Отметим основные моменты идеализации реальных физических систем, допущенные в этом определении. 1. Предполагается, что матрицы системы 2. Рассматриваются линейные уравнения. Реальные системы описываются, как правило, нелинейными уравнениями. Однако, исследование линейных систем имеет важное значение по следующим причинам: а) имеется много динамических систем, движение которых описывается с помощью линейных уравнений; б) линейная теория имеет законченный вид, разработаны достаточно эффективные численные методы решения линейных задач; в) с помощью линейной теории можно изучать нелинейные динамические системы в окрестности их номинальных траекторий. Таким образом, линейная теория служит основой для изучения нелинейных систем. Примеры систем управления и их Математические модели Реальные системы управления, как правило, достаточно сложны. Приведенные ниже примеры используются для иллюстрации основных задач теории управления. Поэтому рассматриваемые системы управления отличаются максимальной простотой и наглядностью. Пример 1.1. Предположим, что некоторая материальная точка Пусть известно, что в начальный момент времени
и в течение всего движения этой точки сила
Можно поставить задачу: определить силу
за минимально возможное время
Согласно второму закону Ньютона уравнение движения точки
Точку
Поставленная задача называется задачей о быстродействии. При решении задач управления пользуются фазовыми координатами и фазовым пространством. В данном случае фазовыми координатами являются две переменные
Фазовые координаты дают возможность записать граничные условия (1.2) и (1.4) в виде
а уравнение (1.6) в виде системы двух дифференциальных уравнений первого порядка
Точка Пример 1.2. Рассмотрим материальную точку массы
где Проектируя уравнение (1.9) на горизонтальную и вертикальнуюоси координат, получим следующие уравнения движения:
где
где
где
|
||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 683; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.01 с.) |

 (1.1)
(1.1) – векторы–столбцы размерности
– векторы–столбцы размерности  соответственно;
соответственно;  – называется входом системы или управлением (управляющим воздействием);
– называется входом системы или управлением (управляющим воздействием);  – выход системы или вектор выходных переменных (выходная величина);
– выход системы или вектор выходных переменных (выходная величина);  – состояние системы или вектор фазовых координат (траектория движения) системы. С другой стороны,
– состояние системы или вектор фазовых координат (траектория движения) системы. С другой стороны,  имеют размерность,
имеют размерность, 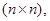

 соответственно. Элементы этих матриц не зависят от времени, в этом случае система (1.1) называется стационарной.
соответственно. Элементы этих матриц не зависят от времени, в этом случае система (1.1) называется стационарной.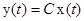 называется уравнением наблюдения линейной системы или уравнением выхода. Оно используется при решении задачи наблюдаемости. При исследовании вопросов устойчивости и управляемости системы это соотношение не учитывается.
называется уравнением наблюдения линейной системы или уравнением выхода. Оно используется при решении задачи наблюдаемости. При исследовании вопросов устойчивости и управляемости системы это соотношение не учитывается. . Для системы (1.1)
. Для системы (1.1)  -мерным векторным пространством
-мерным векторным пространством  .
. называется состоянием системы в момент времени
называется состоянием системы в момент времени 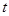 , а координаты этого вектора относительно какого-либо базиса, выбранного в пространстве состояний, называют переменными состояния.
, а координаты этого вектора относительно какого-либо базиса, выбранного в пространстве состояний, называют переменными состояния. обозначим множество моментов времени, для которых рассматривается движение (1.1). Обычно
обозначим множество моментов времени, для которых рассматривается движение (1.1). Обычно  или с полуинтервалом
или с полуинтервалом  .
. называют обычно пространством событий или фазовым пространством. Точка
называют обычно пространством событий или фазовым пространством. Точка  .
.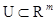 . Заметим, что в качестве множества мгновенных значений управлений рассматривается, вообще говоря, неограниченное множество.
. Заметим, что в качестве множества мгновенных значений управлений рассматривается, вообще говоря, неограниченное множество. в состояние
в состояние  . Под движением системы подразумевается изменение во времени ее состояния, т. е. функцию
. Под движением системы подразумевается изменение во времени ее состояния, т. е. функцию  .
. при любом
при любом  ;
; 
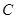 – постоянные матрицы размерности
– постоянные матрицы размерности  массы
массы  может двигаться только по прямой линии, вдоль которой на точку действует сила
может двигаться только по прямой линии, вдоль которой на точку действует сила  . Положение точки
. Положение точки  (рис. 1.1).
(рис. 1.1). выполнены условия
выполнены условия (1.2)
(1.2) . (1.3)
. (1.3)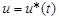 , под действием которой точка
, под действием которой точка  перемещается в другое заданное состояние, например,
перемещается в другое заданное состояние, например, (1.4)
(1.4) . (1.5)
. (1.5) . (1.6)
. (1.6) является управляющим воздействием или управлением.
является управляющим воздействием или управлением.
 и
и  , связанные с переменной
, связанные с переменной  равенствами
равенствами .
. (1.7)
(1.7) (1.8)
(1.8) на плоскости
на плоскости  является фазовой точкой системы (рис. 1.2). С изменением времени
является фазовой точкой системы (рис. 1.2). С изменением времени  , возникающая в результате отделения от нее частиц с элементарной массой
, возникающая в результате отделения от нее частиц с элементарной массой  . Тогда масса точки является величиной переменной
. Тогда масса точки является величиной переменной  и ее движение можно описать векторным уравнением Мещерского [7, с.25], которое соответствует второму закону Ньютона для точки с переменной массой
и ее движение можно описать векторным уравнением Мещерского [7, с.25], которое соответствует второму закону Ньютона для точки с переменной массой , (1.9)
, (1.9) – вектор абсолютной скорости точки
– вектор абсолютной скорости точки  ,
,  – неизменная часть массы точки,
– неизменная часть массы точки,  – реактивная масса точки;
– реактивная масса точки;  ,
,  – вектор относительной скорости отделяющейся частицы;
– вектор относительной скорости отделяющейся частицы;  – вес.
– вес. (1.10)
(1.10)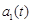 и
и  – проекции вектора
– проекции вектора 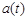 на оси
на оси  и
и  . Допуская, что абсолютная величина вектора
. Допуская, что абсолютная величина вектора  (1.11)
(1.11) ,
,  ,
,  – угол между вектором
– угол между вектором  (рис.1.3). В матричной форме система (1.11) запишется так:
(рис.1.3). В матричной форме система (1.11) запишется так: , (1.12)
, (1.12) .
.



