Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача максимального быстродействияСодержание книги
Поиск на нашем сайте Для задачи о максимальном быстродействии, когда функционалом, минимум которого отыскивается, является время
уравнение для переменного
Заметим, что задачу о минимуме любого функционала (4.2) можно свести к задаче о быстродействии, введя новую переменную
Пользуясь теоремой о максимуме, можно фактически определять оптимальные управления Пример 4.1. Пусть система управления описывается уравнениями вида
где Требуется решить задачу оптимального перевода этой системы из произвольной точки Матрицы
Согласно критерию управляемости исходная система управляема. Можно применить принцип максимума, который в данном случае является необходимым и достаточным условием оптимальности, т.к. эта задача о максимальном быстродействии с начальным состоянием Построим решение указанной задачи оптимального управления в соответствии с принципом максимума. Функция
Из условия максимума (4.6) получим
Функции
Общее решение этой системы можно записать так:
где Проанализируем полученный результат. 1) При
2) При 3) При
4) При 5) При Эти результаты позволяют заключить, что оптимальные траектории системы (4.9) можно построить при управлениях
Аналогично, подставляя в уравнения (4.9) управления На всех семействах траекторий можно выделить те траектории, которые проходят через начало координат. Те части выделенных траекторий, которые оканчиваются в начале координат называются линиями переключений.
Эти линии представлены на рис. 4.3. На рисунке приняты следующие обозначения: линии Изображающая точка, начальное положение которой не лежит на одной из линий переключения, должна перемещаться согласно принципу максимума вдоль одной из линий семейств траекторий в соответствии с системой уравнений (4.9) при определенных значениях управлений
КОНТРОЛЬНАЯ РАБОТА
Вариант 1 Задача 1. Построение импульсной переходной матрицы системы. Линейная динамическая система описывается следующей нормальной системой дифференциальных уравнений:
Построить импульсную переходную матрицу системы с помощью обратного преобразования Лапласа.
|
|||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 1092; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.005 с.) |

 ,
,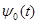 отпадает и функция
отпадает и функция  (4.3) принимает вид
(4.3) принимает вид .
. и дополнительное уравнение
и дополнительное уравнение .
. , доставляющие минимум функционалу (4.2) при учете уравнений связи (4.1).
, доставляющие минимум функционалу (4.2) при учете уравнений связи (4.1). (4.9)
(4.9) – компоненты вектора управления, удовлетворяющие условиям
– компоненты вектора управления, удовлетворяющие условиям 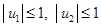 .
. фазового пространства в начало координат.
фазового пространства в начало координат. и
и  в данном случае имеют вид
в данном случае имеют вид ,
,  .
. и конечным состоянием
и конечным состоянием 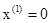 .
. . (4.10)
. (4.10) при
при  ;
; при
при 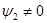 . (4.11)
. (4.11) ,
, 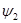 определяются как ненулевое решение сопряженной системы уравнений, которая в этом случае принимает вид
определяются как ненулевое решение сопряженной системы уравнений, которая в этом случае принимает вид . (4.12)
. (4.12) ,
, – произвольные постоянные.
– произвольные постоянные. и
и  функция
функция  , а функция
, а функция  ;
;  вначале равно +1, а затем –1.
вначале равно +1, а затем –1. :
:  .
. и
и  ;
;  .
.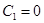 функция
функция 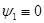 , поэтому в выражении (4.10)
, поэтому в выражении (4.10)  можно положить равным любому допустимому значению. Значение же управления
можно положить равным любому допустимому значению. Значение же управления 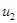 в зависимости от знака постоянной
в зависимости от знака постоянной  может быть равно либо +1, либо –1. Таким образом, в этом случае
может быть равно либо +1, либо –1. Таким образом, в этом случае  – произвольное допустимое;
– произвольное допустимое;  .
.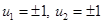 . Подставляя последовательно указанные управления в систему (4.9) и интегрируя ее, получим четыре семейства траекторий, из которых можно построить оптимальную траекторию, ведущую в начало координат. Например, подставляя в (4.9)
. Подставляя последовательно указанные управления в систему (4.9) и интегрируя ее, получим четыре семейства траекторий, из которых можно построить оптимальную траекторию, ведущую в начало координат. Например, подставляя в (4.9)  , получим
, получим
 откуда находим
откуда находим  . После интегрирования этого уравнения определим семейство траекторий
. После интегрирования этого уравнения определим семейство траекторий 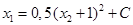 , одна из которых при
, одна из которых при 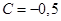 проходит через начало координат. Полученное семейство траекторий изображено на рис. 4.1. На этом же рисунке пунктиром изображено семейство траекторий, соответствующее управлениям
проходит через начало координат. Полученное семейство траекторий изображено на рис. 4.1. На этом же рисунке пунктиром изображено семейство траекторий, соответствующее управлениям  и
и  .
. и
и  , после интегрирования получаем соответственно два семейства фазовых траекторий. Эти фазовые траектории изображены на рис. 4.2.
, после интегрирования получаем соответственно два семейства фазовых траекторий. Эти фазовые траектории изображены на рис. 4.2.
 соответствует часть фазовой траектории при
соответствует часть фазовой траектории при  и
и  , линии
, линии  – при
– при  и
и  – при
– при  , линии
, линии  – при
– при  и
и  до пересечения с одной из линий переключения (рис. 4.3). В момент пересечения происходит переключение управления и движение в дальнейшем будет происходить вдоль линии переключения в начало координат.
до пересечения с одной из линий переключения (рис. 4.3). В момент пересечения происходит переключение управления и движение в дальнейшем будет происходить вдоль линии переключения в начало координат.