
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача с фиксированными концами траекторийСодержание книги
Поиск на нашем сайте Предположим, что на некоторой гладкой одномерной кривой
в котором функцию Определим необходимые условия, которым должна удовлетворять функция Для сравнения функционалов придадим функции Определим приращение функционала
Разложим
где Первый член разложения (3.19) обозначается При
где приняты следующие обозначения:
В то же время, согласно предположению о том, что на кривой
Для того, чтобы неравенство (3.21) выполнялось при любых
Таким образом, необходимым условием экстремума является равенство нулю первой вариации функционала. Проинтегрируем второй член подынтегрального выражения в (3.20) по частям:
Так как
В результате
Теперь к выражению (3.23) применим лемму Лагранжа, которая утверждает: если непрерывная функция На основании леммы Лагранжа из равенства (3.23) можно сделать важный вывод: если
Уравнение (3.24) называется уравнением Эйлера. Оно играет центральную роль в вариационном исчислении. С его помощью можно фактически определить функцию, на которой может достигаться экстремум. Решения уравнения Эйлера называются экстремалями. Общее решение его содержит две неопределенные постоянные, для определения которых требуется удовлетворение двух условий. Как правило, в качестве таких условий задаются значения функции Выполнив полное дифференцирование по
и уравнение Эйлера можно записать в следующем виде:
где
Из (3.25) следует, что в общем случае уравнение Эйлера является нелинейным дифференциальным уравнением второго порядка и поэтому его решить нелегко. Следует заметить, что вывод уравнения Эйлера через лемму Лагранжа можно считать корректным, если заранее предполагается, что у функции Уравнение Эйлера можно проинтегрировать лишь в некоторых частных случаях [9, с.15–18]. В случае многомерной системы необходимыми условиями экстремума функционала
на множестве непрерывно дифференцируемых функций
Решение уравнений Эйлера (3.24) или (3.25) определяет собой возможную экстремаль функционала Действительно, как показывает разложение (3.19), если первая вариация обращается в нуль, то, поскольку при достаточно малом
Поэтому в случае минимума
Второй член этого выражения можно преобразовать, применив интегрирование по частям, с учетом того, что
Следовательно,
где
Но так как для того, чтобы кривая
для максимума необходимо
Для многомерной системы достаточным условием минимума функционала, т.е. условием Лежандра, является условие положительности квадратичной формы
и произвольных
|
||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 452; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.009 с.) |

 , проходящей через точки
, проходящей через точки 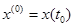 и
и  , достигается слабый относительный минимум функционала
, достигается слабый относительный минимум функционала , (3.17)
, (3.17) предполагаем непрерывной и имеющей непрерывные частные производные по всем аргументам до второго включительно.
предполагаем непрерывной и имеющей непрерывные частные производные по всем аргументам до второго включительно. , где
, где  , а
, а  – произвольная гладкая функция, удовлетворяющая условиям
– произвольная гладкая функция, удовлетворяющая условиям  и
и  , т.е. варьируемая кривая должна проходить через концы интервала.
, т.е. варьируемая кривая должна проходить через концы интервала.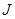 :
: . (3.18)
. (3.18) в ряд Маклорена по степеням
в ряд Маклорена по степеням  :
: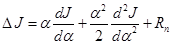 , (3.19)
, (3.19) – остаток более высокого порядка малости относительно первых членов разложения.
– остаток более высокого порядка малости относительно первых членов разложения.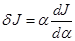 и называется первой вариацией. Первая вариация линейна. Второй член – обозначается
и называется первой вариацией. Первая вариация линейна. Второй член – обозначается 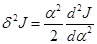 и называется второй вариацией, она нелинейна.
и называется второй вариацией, она нелинейна. , приращение
, приращение  , (3.20)
, (3.20) ;
;  .
.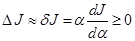 . (3.21)
. (3.21)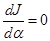 . (3.22)
. (3.22) .
. и
и  , то
, то .
. . (3.23)
. (3.23) обладает тем свойством, что
обладает тем свойством, что 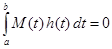 для любой гладкой функции
для любой гладкой функции 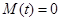 для всех
для всех  .
. . (3.24)
. (3.24) и
и  .
.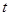 второго члена уравнения (3.24) с учетом того, что
второго члена уравнения (3.24) с учетом того, что  , получим
, получим ,
, , (3.25)
, (3.25)

 .
. , так и вторая производная
, так и вторая производная  .
.
 с фиксированными конечными значениями
с фиксированными конечными значениями 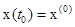 ,
,  при условии двойной дифференцируемости по всем своим аргументам функции
при условии двойной дифференцируемости по всем своим аргументам функции  являются уравнения Эйлера
являются уравнения Эйлера .
. .
. , в случае максимума
, в случае максимума  . Очевидно, что
. Очевидно, что .
. и
и  :
: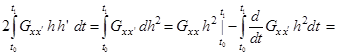
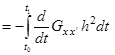 .
. ,
, ;
; 
 , необходимо
, необходимо 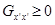 . Действительно, легко подобрать такую функцию
. Действительно, легко подобрать такую функцию  было мало, а
было мало, а  велико. Для такой функции знак второй вариации будет совпадать со знаком
велико. Для такой функции знак второй вариации будет совпадать со знаком  , и мы приходим к следующему необходимому условию (условию Лежандра):
, и мы приходим к следующему необходимому условию (условию Лежандра): , должно выполняться неравенство
, должно выполняться неравенство ; (3.26)
; (3.26) . (3.27)
. (3.27) при
при 
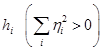 .
.


