
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постановка задачи об управляемостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рассмотрим задачу об управляемости многомерными системами, функционирование которых описывается нормальной системой линейных дифференциальных уравнений. Система уравнений в матричной форме имеет следующий вид:
где Определение. Система (2.1) называется вполне управляемой, если для двух произвольных точек Пусть
Теорема 2.1. Для того, чтобы система (2.1) была вполне управляемой, необходимо и достаточно, чтобы вектор–строки матриц Доказательство теоремы построено на формуле Коши для уравнения (2.1) с начальным условием
Однако необходимые и достаточные условия управляемости системы (2.1), сформулированные в этой теореме, практически трудно использовать для исследования конкретных систем управления в связи с тем, что определение матрицы Критерий управляемости В стационарном случае критерий управляемости принимает простую и компактную форму. Пусть заданы матрицы системы
Управляемость стационарной системы (2.1) связанасо свойствами матрицы Лемма 2.1. Если ранг матрицы Доказательство этой леммы можно найти в [4, с.86]. Из этой леммы, в частности, следует, что прибавление каждого последующего элемента вида Сформулируем теперь основной (в смысле управляемости) результат теории линейных стационарных систем. Теорема 2.2. (критерий управляемости стационарной системы). Линейная стационарная п-мерная система (2.1) вполне управляема тогда и только тогда, когда ранг Доказательство. Достаточность. Предположим, что ранг матрицы
Сформулированное утверждение равнозначно следующему: если существует некоторый отрезок Для доказательства последнего утверждения продифференцируем
Учитывая формулу (1.20), можем записать
где Известно [4, с.62], что матрица
а поэтому имеем
или
Используя свойство (2.6), из равенств (2.5) легко получить соотношения
Положив здесь
Это в свою очередь возможно только в том случае, если ранг матрицы Необходимость условий теоремы будет установлена, если докажем, что из линейной независимости вектор-функции (2.2) при Предположим, что ранг матрицы
Учитывая утверждение леммы 2.1, приходим к выводу, что
для всех целых Принимая во внимание, что матрицу
то для линейной комбинации векторов (2.4) получим выражение
Если в этом равенстве за вектор
что означает линейную зависимость векторов (2.2). Замечание. В случае, если вектор управления в системе (2.1) одномерный, матрица
Соотношения (2.3) и (2.10) назовем условиями вполне управляемости стационарных систем. Определение. Система (2.1) называется вполне управляемой на заданном промежутке
Согласно доказанной теореме 2.2 свойство управляемости системы полностью определяется алгебраическими свойствами пары матриц
|
||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 540; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.009 с.) |

 , (2.1)
, (2.1) – векторы-столбцы размерности
– векторы-столбцы размерности  и
и  соответственно;
соответственно;  – постоянные матрицы размерности
– постоянные матрицы размерности  и
и  соответственно.
соответственно. и
и  из фазового пространства
из фазового пространства  и двух произвольных значений
и двух произвольных значений  и
и  аргумента
аргумента 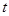 существует такая функция управления
существует такая функция управления 
 , при которой решение уравнения (2.1) удовлетворяет условиям
, при которой решение уравнения (2.1) удовлетворяет условиям  и
и  .
. – фундаментальная матрица однородной системы уравнениям (2.1). Тогда матрица импульсных переходных функций
– фундаментальная матрица однородной системы уравнениям (2.1). Тогда матрица импульсных переходных функций  и нормированная фундаментальная матрица
и нормированная фундаментальная матрица  . (2.2)
. (2.2)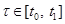 были линейно независимыми на всяком произвольном промежутке
были линейно независимыми на всяком произвольном промежутке  .
. .
. и
и  .
.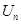 размером
размером  , первые
, первые  (или просто
(или просто  ) и т. д., последние
) и т. д., последние 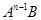 . Матрицу
. Матрицу 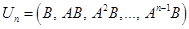 .
. равен рангу матрицы
равен рангу матрицы  , то дальнейшее прибавление столбцов вида
, то дальнейшее прибавление столбцов вида  ,
,  , не увеличивает ранга матрицы.
, не увеличивает ранга матрицы. либо увеличивает ранг матрицы на некоторое постоянное число, либо не меняет ранга. В последнем случае и прибавление всех последующих столбцов вида
либо увеличивает ранг матрицы на некоторое постоянное число, либо не меняет ранга. В последнем случае и прибавление всех последующих столбцов вида  . (2.3)
. (2.3) матрицы
матрицы  при
при  и
и  линейно независимы на произвольном интервале
линейно независимы на произвольном интервале 
 , что имеет место тождество
, что имеет место тождество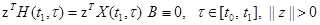 . (2.4)
. (2.4) раз тождество (2.4) по переменной
раз тождество (2.4) по переменной 
 (2.5)
(2.5) ,
, – обратная матрица по отношению к матрице
– обратная матрица по отношению к матрице  фундаментальных решений однородного уравнения для уравнения (2.1).
фундаментальных решений однородного уравнения для уравнения (2.1). удовлетворяет уравнению
удовлетворяет уравнению ,
,
 . (2.6)
. (2.6)
 , имеем
, имеем (2.7)
(2.7) вытекает равенство ранга матрицы
вытекает равенство ранга матрицы  , что
, что . (2.8)
. (2.8) (2.9)
(2.9) .
. ,
, .
. ,
,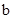 , а поэтому необходимое и достаточное условие вполне управляемости принимает форму
, а поэтому необходимое и достаточное условие вполне управляемости принимает форму . (2.10)
. (2.10) и
и  из фазового пространства
из фазового пространства  можно указать такую функцию управления
можно указать такую функцию управления  , что решение уравнения(1) удовлетворяет краевым условиям
, что решение уравнения(1) удовлетворяет краевым условиям и
и  .
. . Именно, если матрица
. Именно, если матрица  , составленная указанным выше образом, имеет полный ранг, то система управляема.
, составленная указанным выше образом, имеет полный ранг, то система управляема.


