
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Управляемость и стабилизируемость системСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Управляемость. Общие положения При создании систем управления необходимо установить возможность перевода объекта из заданной начальной точки или области в заданную конечную точку или область, т.е. управляемость системы. Управляемость зависит от структуры системы, состава органов управления, значений параметров, располагаемой энергии управления. В простых случаях эта задача решается интуитивно на основе опыта и знаний. Однако в сложных случаях возможны ошибки при выборе структуры управления, в результате чего объект управления не будет обладать указанными свойствами. Существуют различные виды управляемости в зависимости от условий перехода и ограничений, накладываемых на управление. Типы переходов иллюстрируются рис. 1.7. В случае (рис. 1.7а) рассматривается переход из произвольной точки n-мерного пространства состояний, в произвольную точку этого пространства, причем никаких ограничений на характер движения, кроме конечности времени перехода ti – t0, не накладывается ( Переход из заданной области пространства состояний полной размерности n в заданную область меньшей размерности иллюстрируется рис. 1.7г. Противоположным предыдущему, является случай, когда управление должно обеспечить перевод системы из любой точки области меньшей размерности в любую точку области полноразмерной области (рис. 1.7в). Рис. 1.7д соответствует управляемости в малом. Управление должно обеспечить переход из любой точки Х0 пространства состояний Rn в любую точку малой n-мерной окрестности Случай (рис. 1.7е) соответствует переходу из заданной области подпространства меньшей размерности m<n в замкнутую область того же подпространства (случай неполной управляемости). Важное практическое значение имеет случай, когда задается множество программных траекторий Х0(t) перехода из одной точки Х0(t0) в другую Х0(t1). Система считается управляемой, если существуют управления, обеспечивающие движение по заданной траектории при условии: Х(t0)= Х0(t0), Х(t1)= Х0(t1). Определим свойство управляемости и установим критерий управляемости. Пусть объект задан уравнением:
где Х – вектор фазовых координат, U – вектор управления, Rn, Rr – пространства фазовых координат и допустимых управлений соответственно. При этом допустимое множество Ut значений управления совпадает со всем пространством Rr, и допустимым управлением является любая кусочно-непрерывная вектор-функция, принимающая значения из Rr. Объект называется вполне или полностью управляемым, если для любой пары точек Х0 и Хf на Rn существует допустимое управление на конечном интервале [t0, tf], переводящее объект из точки X(t0)=X0 в точку X(tf)=Xf.
Для линейного стационарного объекта можно принять t0=0 и зафиксировать одну из точек, например, положить Х0=0 или Xf=0. Уравнение линейного объекта
где А, В – матрицы коэффициентов. При произвольном начальном условии решение уравнения (1.124) имеет вид:
При Х0=0
где К(t,τ) – переходная матрица системы. Тогда задача перевода объекта (1.124) из произвольной начальной точки X(t0)=X0 в точку X(tf)=Xf равносильна задаче его перевода из начальной точки X(t0)=0 в точку X(tf)=Xf – К(tf, t0)Х0. Аналогично, задача перевода объекта (1.124) из начальной точки X(t0)=X0 в произвольную конечную точку X(tf)=Xf равносильна задаче его перевода из начальной точки X(t0)=К0-Х-1(tf,t0) в точку X(tf)=0. Объект называется вполне управляемым, если для любой точки Xf из Rn существует допустимое управление на конечном интервале [t0,tf], переводящее объект из точки X(t0)=0 в точку X(tf)=Xf, или объект называется вполне управляемым, если для любой точки Xf из Rn существует допустимое управление на конечном интервале [t0,tf], переводящее объект из точки X(t0)=X0 в точку X(tf)=0. 1.2.2.Критерии управляемости Для нестационарного линейного объекта
где A(t),B(t) – матрицы коэффициентов. Решение уравнения (1.127) будем искать в виде х=Ху, где Х=Х(t) – решение уравнения
Поэтому
Интегрирование последнего уравнения дает решение:
а, следовательно, для х=Ху получим
Используя свойство решения Х(t0)=I, а, значит, и Х-1(t0)=I, можно записать
и ввести матрицу Коши для системы (1.127) К(t,s)=Х(t)Х-1(s), К(t0,t0)=Е. Матрица Коши обладает очевидным свойством К(t0,t0)= К(t,s) К(s,t0). Таким образом, решение системы уравнений (1.127) можно представить в виде
Объект называется вполне управляемым, если для любой точки Хf из rn существует допустимое управление на конечном интервале [t0,t1], переводящее любой объект из точки Х(t0)=0 в точку Х(tf)=Хf, или объект называется вполне управляемым, если для любой точки Х0 из rn существует допустимое управление на конечном интервале [t0,tf], переводящее объект из точки Х(t0)=Х0 в точку Х(tf)=0. Рассмотрим критерий управляемости для линейных непрерывных систем. Теорема. Непрерывная линейная система (1.124) является полностью управляемой тогда и только тогда, когда симметрическая матрица размера nхn
положительно определена для некоторого t1>t0. Доказательство. Прежде всего, рассмотрим квадратную форму
где Очевидно, что r=кв есть некоторая матрица, а Таким образом,
а следовательно, матрица n как минимум положительно полуопределена и для положительной определенности нужно доказать ее невырожденность. Достаточность. Из уравнения (1.125) для t=tf получим
В качестве управления выберем функцию
где у – некоторый вектор. Подставим u(
Тогда, учитывая, что матрица n не вырождена, а следовательно, существует n-1, пусть
Подставив (1.132) в (1.130) и (1.129), получим
Это требуемый результат и, как следствие, система является управляемой. Необходимость. Полагаем, что система (1.124) управляема, т.е. независимо от начального состояния Х0 может быть реализовано управление u(t), обеспечивающее переход из (t0, х0) в состояние (tf, хf). Для простоты осуществим переход из х0=0 в хf
После интегрирования левой и правой частей получим
Обращаясь к (1.128), можем записать
и считаем, что матрица является вырожденной, т.е.
а это противоречит понятию управляемости. Тогда в (1.133) мы должны положить, что n(tf, t0) является невырожденной матрицей. Отметим, что управляемость является свойством динамической системы и не зависит от избранной системы координат, т.е. не зависит от канонической формы представления системы. Можно отметить также, что функция (1.130)
представляет собой закон управления с целью перехода системы из заданного начального положения к началу координат. Отсюда очевидна связь понятий управляемости и управления. Можно также показать, что функция (1.130) минимизирует «работу» управления Для стационарных систем вопрос об управляемости может быть решен на основе следствия рассмотренной теоремы. 1.2.3.Управляемость линейных стационарных объектов Введем в рассмотрение матрицу управляемости размером (nхnr) Y=[B AB A2B … An-1B]. (1.135) Справедлив следующий критерий управляемости: линейный стационарный объект (1.124) вполне управляем тогда и только тогда, когда ранг матрицы управляемости равен n. В соответствии с теоремой Гамильтона-Кэли, любая квадратная матрица удовлетворяет своему характеристическому уравнению. Так как характеристическое уравнение матрицы А имеет вид: det(SE-A)=Sn-C1Sn-1-C2Sn-2-…-Cn=0, то, используя теорему, можно записать для матрицы А соотношение An=C1An-1+C2An-2+…+CnE. (1.136) Докажем необходимость и достаточность утверждения. Необходимость. Известно, что система вида
Учитывая, что показательная функция em разлагается в ряд Тейлора следующего вида
можно еАt представить в виде
обозначим в (1.137)
Тогда при х(0)=0 из (1.137) с учетом (1.138) получаем для х(tf)
Умножив обе части равенства (1.136) справа на В, получим
Умножим обе части последнего равенства на А
Подставим в последнее равенство выражение для АnВ
или
Проделав аналогичные операции l раз будем иметь
т.е. при любом l An+1B является линейной комбинацией матриц AкB, Таким образом, Х(tf) представляется в виде линейной комбинации векторов, представляющих собой столбцы матрицы управляемости (1.135) и при любом допустимом управлении точка Х(tf) принадлежит подпространству, порожденному столбцами матрицы управляемости Y. Поэтому, если ранг матрицы Y меньше n, то существуют точки, не принадлежащие указанному подпространству, куда нельзя перевести объект (1.124) из точки Х(0)=0. Достаточность. Пусть ранг матрицы Y равен n. При Х(0)=0 и t= tf имеем
Объект вполне управляем, если приведенное интегральное уравнение при произвольном хf и rn имеет решение в классе допустимых управлений. Будем искать решение в виде
где z – вектор из rn. Подставив это выражение в интегральное уравнение, получим Х=Dz, где
Таким образом, вопрос о существовании решения интегрального уравнения свелся к вопросу о существовании решения алгебраического уравнения. Это уравнение имеет решение при произвольном хf, если det D Допустим противное: det(D)=0. Тогда соответствующее однородное уравнение имеет ненулевое решение, т.е. существует вектор хL≠0 такой, что Умножив слева на
В силу непрерывности подинтегрального выражения последнее равенство возможно, если при всех
Но, учитывая, что
после дифференцирования (1.139) по
или при
Заметим, что Из последних равенств следует, что ненулевой вектор Таким образом, управляемость объекта полностью определяется матрицами А и В. Поэтому критерий управляемости можно сформулировать следующим образом: пара (А,В), в которой А и В - матрицы размерности Свойство управляемости не зависит от выбора системы координат. Если объект вполне управляем, то его область управляемости совпадает со всем фазовым пространством. 1.2.4.Каноническая форма управляемости Если объект не вполне управляем, то он не может быть переведён из точки
такую, что
и вектор-столбец матрицы В качестве Используя (1.140), преобразуем (1.124)
где Для обратной матрицы
где
Учитывая определение обратной матрицы
откуда следует, что
Таким образом, из (1.143) можно утверждать, что все вектор - столбцы Тогда для (1.141) можно записать
Так как все вектор - столбцы матрицы Следовательно, используя первое из соотношений (1.143) и не забывая, что
Очевидно, что
Учтём также, что все вектор - столбцы матрицы В лежат в
Следовательно, поведение
Структурная схема вполне управляемой системы S, которую формально можно разбить на две подсистемы  и и  , может быть представлена, как на рис. 1.8а. Если же управляющее воздействие U не подаётся на вход подсистемы , может быть представлена, как на рис. 1.8а. Если же управляющее воздействие U не подаётся на вход подсистемы  и отсутствует связь и отсутствует связь  , то получим пример не вполне управляемой системы (рис. 1.8б). , то получим пример не вполне управляемой системы (рис. 1.8б).
Для иллюстрации приведения к канонической форме рассмотрим систему:
Матрица управляемости и её ранг равны:
Следовательно, система не вполне управляема. Неуправляемой координатой является Матрица Т принимает вид
Обратная матрица
Отсюда следует
1.2.5.Стабилизируемость Если линейный объект не вполне управляем, то его вектор состояния можно представить в виде
где Из ранее доказанного критерия управляемости следует, что объект не может быть переведён из точки Стационарный линейный объект
называется стабилизируемым, если в представлении Очевидно, что вполне управляемый объект является стабилизируемым, так как x=0. Асимптотически устойчивый объект является стабилизируемым, так как при В случае канонической формы управляемости составляющая имеет вид
поэтому в этой системе координат Из канонической формы управляемости видно, что объект является стабилизируемым в том и только в том случае, если матрица Пример 1.6. Смесительный бак (см. пример 1.2) при условии
Как было показано, эта система не является управляемой. Матрица
|
||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 1164; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.01 с.) |

 ). Если в пространстве состояний задана замкнутая область G и должен обеспечиваться переход из любой точки этой области в произвольную точку без выхода за пределы области G, то существует ограничение типа неравенств в пространстве состояний (рис. 1.7б) этой области в произвольную точку без выхода за пределы области G, то существует ограничение типа неравенств в пространстве состояний (рис. 1.7б).
). Если в пространстве состояний задана замкнутая область G и должен обеспечиваться переход из любой точки этой области в произвольную точку без выхода за пределы области G, то существует ограничение типа неравенств в пространстве состояний (рис. 1.7б) этой области в произвольную точку без выхода за пределы области G, то существует ограничение типа неравенств в пространстве состояний (рис. 1.7б). точки Х0 (
точки Х0 ( ).
).
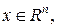
 ,
,

 (1.124)
(1.124) . (1.125)
. (1.125) , (1.126)
, (1.126)
 ,
, 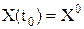 , (1.127)
, (1.127) . Подстановка в (1.127) дает уравнение
. Подстановка в (1.127) дает уравнение
 .
. .
.
 .
.

 , (1.128)
, (1.128)
 – некоторый вектор состояния.
– некоторый вектор состояния. – вектор-строка
– вектор-строка  . Тогда
. Тогда  – есть вектор-столбец.
– есть вектор-столбец.
 . (1.129).
. (1.129). (1.130),
(1.130), ) в уравнение (1.129)
) в уравнение (1.129) .(1.131)
.(1.131) . (1.132).
. (1.132). .
. 0. Для этого используем управление из (1.130) и запишем
0. Для этого используем управление из (1.130) и запишем .
.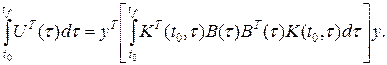
 , (1.133)
, (1.133) Так как
Так как  – непрерывны, то из (1.133) следует, что
– непрерывны, то из (1.133) следует, что  =0 и, подставив в (1.129) и учитывая, что х0=0, получим
=0 и, подставив в (1.129) и учитывая, что х0=0, получим ,
, , (1.134)
, (1.134) при переходе из х(t0) к началу координат на фиксированном отрезке [t0,tf], т.е. получено решение частной задачи оптимального управления, о котором речь пойдет несколько позже.
при переходе из х(t0) к началу координат на фиксированном отрезке [t0,tf], т.е. получено решение частной задачи оптимального управления, о котором речь пойдет несколько позже. имеет переходную матрицу
имеет переходную матрицу  поэтому решение уравнения имеет следующий вид:
поэтому решение уравнения имеет следующий вид: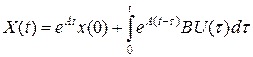 . (1.137)
. (1.137) ,
, , (1.138)
, (1.138) .
.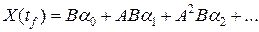
 .
. .
. ,
, .
.
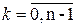 .
.



 и подставив выражение для D, получим
и подставив выражение для D, получим .
.
 . (1.139)
. (1.139) ,
, , получим
, получим ,
,
 .
. .
. ортогонален всем вектор - столбцам матрицы управляемости У, а это невозможно, так как по условиям ранг матрицы У равен n. Следовательно, допущение о том, что
ортогонален всем вектор - столбцам матрицы управляемости У, а это невозможно, так как по условиям ранг матрицы У равен n. Следовательно, допущение о том, что  , неверно. Критерий управляемости доказан.
, неверно. Критерий управляемости доказан. и
и 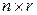 соответственно, называются вполне управляемой, если объект вполне управляем.
соответственно, называются вполне управляемой, если объект вполне управляем. в точку, которая не принадлежит подпространству
в точку, которая не принадлежит подпространству 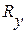 , порождённому вектор – столбцами матрицы управляемости У. Область управляемости совпадает с подпространством
, порождённому вектор – столбцами матрицы управляемости У. Область управляемости совпадает с подпространством 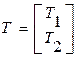 , (1.140)
, (1.140)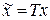 , причём
, причём ,
,  ,
,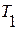 образуют базис l-мерного пространства, а вектор – столбцы
образуют базис l-мерного пространства, а вектор – столбцы 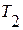 вместе с вектор - столбцами
вместе с вектор - столбцами 
 (1.141)
(1.141) можем произвести разбиение на подматрицы
можем произвести разбиение на подматрицы  и
и 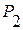 следующим образом:
следующим образом: ,
, .
. ,можем получить
,можем получить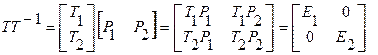 , (1.142)
, (1.142) . (1.143)
. (1.143) из
из 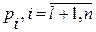 из
из  , напротив, лежат только вне
, напротив, лежат только вне 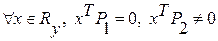 .
. ,
,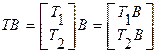 . (1.144)
. (1.144)
 лежат в
лежат в  , которая соответствует неуправляемой координате
, которая соответствует неуправляемой координате  , так как
, так как  состоит из вектор – столбцов, лежащих строго в
состоит из вектор – столбцов, лежащих строго в  .
. состоит из вектор - столбцов, которые могут содержать ненулевые элементы, соответствующие управляемым координатам. Следовательно, в общем случае
состоит из вектор - столбцов, которые могут содержать ненулевые элементы, соответствующие управляемым координатам. Следовательно, в общем случае .
. , так как все элементы строк, соответствующие неуправляемым координатам, должны быть равными нулю. (Иначе, просто неуправляемость по этим координатам нарушается). Тогда
, так как все элементы строк, соответствующие неуправляемым координатам, должны быть равными нулю. (Иначе, просто неуправляемость по этим координатам нарушается). Тогда  и, учитывая все предыдущее, (1.141) принимает вид
и, учитывая все предыдущее, (1.141) принимает вид . (1.145)
. (1.145) полностью независимо, тогда как на
полностью независимо, тогда как на  оказывает влияние
оказывает влияние 


 . Тогда в качестве базиса в
. Тогда в качестве базиса в 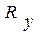 можем принять строки:
можем принять строки:  , которые дополним строкой
, которые дополним строкой  .
.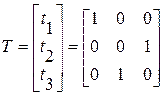 .
.
 .
. ,
, – вектор ортогональный всем элементам из
– вектор ортогональный всем элементам из  , называемого подпространством неуправляемости.
, называемого подпространством неуправляемости.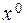 в точку
в точку  , если
, если  или
или  принадлежат
принадлежат  ,
, при
при 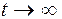 .
.
 , тогда U(t)=0.
, тогда U(t)=0. ,
,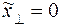 только при
только при  .
. является асимптотически устойчивой, т.е. её собственные значения отрицательные вещественные части. Стабилизируемость объекта полностью определяется матрицами А и В.
является асимптотически устойчивой, т.е. её собственные значения отрицательные вещественные части. Стабилизируемость объекта полностью определяется матрицами А и В. описывается дифференциальным уравнением состояния
описывается дифференциальным уравнением состояния
 , откуда следует, что система является стабилизируемой. Это означает, что при неправильном значении приращения концентрации оно в итоге будет стремиться к нулю.
, откуда следует, что система является стабилизируемой. Это означает, что при неправильном значении приращения концентрации оно в итоге будет стремиться к нулю.


