
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение задач оптимального управления на основе методов вариационного исчисления.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задача с закрепленными концами и фиксированным временем Она формулируется как задача Лагранжа: требуется отыскать допустимую пару (х, u), где х - вектор состояния, а u - вектор управления, таких, чтобы:
В этом случае функция Лагранжа (1.238) имеет вид
а уравнение Эйлера-Лагранжа
Если ввести функцию Гамильтона
то
Задача с подвижными концами и фиксированным временем. В этом случае задача оптимального управления может быть задачей Лагранжа, Больца и Майера. Формулируется она следующим образом: найти допустимую пару (х, u) таких, чтобы
Используя прием Лагранжа, преобразуем эту задачу в простейшую задачу Больца:
где
В этом случае уравнения Эйлера совпадают с (1.244) и (1.246), но одновременно появляются в соответствии с условиями трансверсальности (1.230) дополнительные уравнения, которые легко получить из (1.230), заменив fo на L:
Задача с нефиксированным временем. В этой задаче, в отличие от (1.247), в явном виде могут входить начальный и конечный моменты времени, и она формулируется следующим образом: найти допустимую пару (х, u) таких, чтобы
После преобразования этой задачи в задачу Больца получим
где G и L имеют прежнюю структуру, а уравнение Эйлера совпадает с (1.244) или (1.246), кроме того, должны быть включены условия трансверсальности (1.249), которые в связи с вариацией начального и конечного моментов времени дополняются (учитывая (1.251), (1.243), (1.245)) уравнениями в соответствии с (1.233):
Пример 1.11. Уравнение системы Минимизировать Решение. Уравнение объекта
причем
Матрица управляемости
следовательно, система управляема. Для определения оптимального управления воспользуемся методом вариационного исчисления (формула Лагранжа-Эйлера). Функция Лагранжа
Неизвестные С1 и С2 определяются из краевых условий. Для этого найдем законы изменения фазовых координат. Подставляя управление в уравнение объекта и интегрируя обе части, определим закон изменения координаты
Аналогично из уравнения объекта, найдем
Решая краевую задачу, определим С1, С2, С3, С4.
Оптимальное управление имеет вид:
Пример 1.12. Система описывается уравнением
где Оценить управляемость системы. Найти управление U(t) такое, что Решение. Управляемость
Функция Лагранжа
Гамильтониан
Из второго уравнения системы следует
Из граничных условий определяем
Из условия
Из
Из граничных условий
Из системы уравнений
находим
После подстановки
Тогда оптимальное управление имеет вид:
Пример 1.13. Уравнение системы
Найти, используя уравнение Эйлера – Лагранжа, оптимальные u(t), минимизирующие Решение. Составим гамильтониан
Из уравнений Эйлера-Лагранжа:
имеем
Найденное управление u подставим в уравнение объекта. Решая систему, найдем:
Используя краевые условия, определим С1, С2, С3, С4:
Ответ: Пример 1.14. Найти U(t), минимизирующее при неопределенном
для системы Решение. Составим гамильтониан:
Уравнения Эйлера-Лагранжа имеют вид:
Составим характеристическое уравнение
Используя граничные условия, получим:
Так как в задаче конечный момент времени
Подставляя вместо
Решим уравнения 1)
пусть
Условию y>1 удовлетворяет корень
2) Для второго корня
пусть
Корни данного уравнения не удовлетворяют условию y>1. Далее найдем
Пусть Ответ:
где Пример 1.15. Уравнение системы
Найти, используя уравнение Эйлера – Лагранжа, оптимальные u(t), минимизирующие
Решение. Составим гамильтониан:
Из уравнений Эйлера-Лагранжа:
получим:
Найденное управление u подставим в уравнение объекта. Решая систему, найдем:
Используя краевые условия, определим С1, С2, С3, С4:
Так как координата
Тогда оптимальное управление имеет вид Пример 1.16. Уравнение системы Найти, используя уравнение Эйлера – Лагранжа и условия трансверсальности, оптимальное управление u(t), минимизирующее Решение. Запишем гамильтониан
Так как координаты
С учетом ограничения, наложенного на координату
После подстановки Решая это уравнение, получим два корня Пусть
Ответ:
Контрольные вопросы и задания 1. Сформулируйте общую постановку задачи оптимального управления. 2. Приведите классификацию задач оптимального управления. 3. Какие задачи различают в зависимости от критерия оптимальности? 4. Сформулируйте задачу Лагранжа и покажите метод ее решения. 5. Чем отличается задача с подвижными концами и фиксированным временем от задачи Лагранжа? Сформулируйте ее постановку и укажите особенности метода решения задачи. 6. Что означают условия трансверсальности? 7. В чем заключается особенность задач с нефиксированным временем? Сформулируйте постановку задачи. Какие дополнительные условия при этом следует учитывать? 8. Определите оптимальное управление объектом заданным уравнением
9. В процессе перехода из фиксированного начального
10.Определить оптимальное управление объектом
1.4.5.Принцип максимума Понтрягина В прикладных задачах зачастую на управление накладывают ограничения типа неравенств. В таких задачах управление может иметь разрывы. Метод множителей Лагранжа не позволяет определить число и местоположение точек разрыва, и поэтому в таких случаях он не позволяет находить оптимальное управление. Такие задачи эффективно решаются с помощью принципа максимума, который Л.С.Понтрягин сформулировал в 1953 году как необходимое условие экстремума для задач оптимального управления. Задача с закрепленными концами и фиксированным временем. При отсутствии ограничений на фазовые координаты задачу оптимального управления можно сформулировать как задачу Лагранжа:
Все функции fi непрерывны по Xi, Uj, t и непрерывно дифференцируемы no x1,...,xn, t. Отличие от соответствующей задачи Лагранжа заключается в том, что ограничение задается в виде включения uÎU, где U - допустимое множество значений управления, и не требуется гладкость (непрерывная дифференцируемость) функций f± по управлению. Допустимым принимается управление u(t), принадлежащее к классу кусочно-непрерывных функций и принимающее значения из допустимого множества U. Фазовая траектория называется допустимой, если она является кусочно-гладкой. Пара (u(t)rx(t)) называется допустимой для задачи (1.253), если u(t) и x(t) являются допустимыми управлением и траекторией и x(t) при u(t)= x(t) удовлетворяет уравнениям и краевым условиям этой задачи. Составим функцию Лагранжа:
где Гамильтониан
назван функцией Понтрягина и отличается от Н в вариационных задачах отсутствием ограничений на управление, имеющих в данном случае вид включения u Î U. Тогда задача сводится к следующей:
Функционал J максимизируется, хотя функционал J в исходной задаче минимизируется, так как множитель y0= -1. Пусть (х*(t),u*(t),у*(t)) - решение задачи (1.256). Тогда задача (1.256) равносильна следующим двум:
С учетом (1.254) эти выражения будут иметь вид
Граничные условия для (1.257), (1.258) те же (1.256). Задача (1.257) - простейшая задача вариационного исчисления. Для нее необходимые условия имеют вид
Решение задачи (1.258) очевидно: управление u* доставляет максимум в этой задаче в том и только в том случае, если всюду на [t0, tf], кроме точек разрыва u*(t), выполнено равенство
Условия задачи (1.257) совместно с условием (1.261) составляют необходимые условия задачи (1.253), называемые принципом максимума Понтрягина. Уравнения (1.260) совпадает с уравнениями объекта и поэтому их можно не рассматривать. Уравнения (1.259) называют сопряженными уравнениями или сопряженной системой. Принцип максимума. Для того, чтобы допустимая для задачи (1.253) пара (u*(t), x*(t)) была решением, необходимо, чтобы существовали такие не обращающиеся одновременно в нуль константа Задача с подвижными концами Рассмотрим следующую задачу Больца:
Функции Приемом Лагранжа эту задачу можно свести к следующей простейшей вариационной задаче:
где Как и в случае задачи с закрепленными концами, последняя задача расщепляется на две и получаются необходимые условия в форме принципа максимума. Допустимая пара (u(t), х(t)) для задачи (1.262) определяется так же, как и для задачи (1.253). Принцип максимума. Для того, чтобы допустимая для задачи (1.262) пара (u*(t),x*(t),t Î [t0,tf]), была ее решением, необходимо: 1) существование таких необращающихся одновременно в нуль константы 2) выполнение условий трансверсальности (1.249), (1.252). Рассмотрим связь между принципом максимума и методом множителей Лагранжа. Функция Понтрягина (1.255) отличается от гамильтониана, введенного ранее тем, что в ней не учтено ограничение на управление. Сопряженные уравнения (1.259) совпадают с уравнениями Эйлера-Лагранжа Задача максимального быстродействия Эта задача формулируется следующим образом: найти допустимое управление, переводящее заданный объект из начальной точки (множества) в конечную (конечное множество) за минимальное время. Она является частным случаем задачи с подвижными концами и нефиксированным временем. Если положить t0=0, то критерий оптимальности имеет вид J=tf, поэтому в данном случае g0=tff f0=0 и функция Понтрягина
Рассмотрим задачу максимального быстродействия, когда объект описывается линейными дифференциальными уравнениями:
Эта задача называется линейной задачей максимального быстродействия. В матричной форме уравнения объекта имеют вид
Предполагается, что эти уравнения являются уравнениями в отклонениях, поэтому конечное состояние, в которое нужно перевести объект, есть начало координат (x(tf)). Функция Понтрягина
где
или сопряженной системе уравнений
Согласно принципу максимума, оптимальное управление находят из условия
где Если выполняются так называемые условия нормальности, то сумма В этом случае из последнего тождества следует, что координаты
В частном случае, когда ограничение имеет вид
Условие оптимальности. Введем в рассмотрение (n´n) матрицы Для объекта Теорема об n интервалах. Если в линейной задаче максимального быстродействия объект является нормальным, и его характеристическое уравнение det (A-sE)=0 имеет только действительные корни, то оптимальное управление Если характеристическое уравнение имеет комплексные корни, то число переключений зависит от начальных условий. Оно может быть сколь угодно большим, но конечным. Пример 1.17. Требуется за минимальное время достичь заданного перемещения по координате
Граничные условия Решение. Так как объект требуется перевести из начального состояния в конечное за минимальное время, то функционал примет вид:
Составим гамильтониан:
Гамильтониан достигает максимального значения в том случае, если управление по знаку совпадает с функцией f2, тогда:
Найдем момент переключения. Момент переключения для
Момент переключения для
Решая уравнение, получим:
Составим уравнение
Получим Ответ: Момент переключения
Пример 1.18. Требуется за заданное время Т достичь максимальное перемещение по координате Состояние системы описывается уравнениями:
Найти Решение Используем принцип максимума Понтрягина. Задача с подвижным правым концом. Приведем к задаче Больца.
Функция Понтрягина
Условие максимума
Откуда
Условия трансверсальности (правый конец)
где
Определим точку разрыва (момент переключения)
откуда получаем:
Определим траекторию
В момент переключения
Ответ:
Контрольные вопросы 1. Какова область применения метода оптимизации с использованием принципа максимума Понтрягина? 2. Сформулируйте задачу оптимизации при фиксированном времени с закрепленными концами. 3. Приведите необходимые условия принципа максимума и сформулируйте его. 4. Каковы особенности задачи оптимизации с подвижными концами. Сформулируйте принцип максимума для этой задачи. 5. Дайте формулировку задачи оптимального быстродействия. Сформулируйте ее постановку. 6. Приведите условия решения задачи оптимального быстродействия. 7. Определите оптимальное по быстродействию управление объектом, уравнение которого представляет колебательное звено
где р - постоянная. 1.4.6.Метод динамического программирования Этот метод стабилизации многошаговых процессов, основу которого составляют: - принцип оптимальности; - инвариантное погружение; - функциональное управление, получаемое на основе принципа оптимальности и инвариантного погружения. Основная идея метода заключается в следующем. Вместо решения исходной задачи ее включают в некоторое семейство задач оптимизации (инвариантное погружение). При этом может оказаться, что между отдельными задачами существуют простые соотношения и среди задач найдутся такие, которые легко решаются. Тогда, используя решение и соотношения, связывающие отдельные семейства, получают решение исходной задачи. Например, требуется найти минимум функции вида:
где
В последнем соотношении
В (1.265) параметр m можно рассматривать как дискретное время Введем так называемую функцию Беллмана
Очевидно
Но второе слагаемое в последнем выражении есть Вга, поэтому функция Беллмана удовлетворяет функциональному уравнению
или в силу независимости Вm от xm+1
причем Решая (1.266) с учетом последнего условия, получим Таким образом, метод динамического программирования сводит задачу минимизации скалярных функций от n переменных к n задачам минимизации скалярных функций одной переменной. В результате существенно снижается объем вычислений. При числовом решении задачи без использования метода динамического программирования при Gi (i=1,...,n) - конечных множествах, состоящих каждая из i точек, методом перебора потребовалось бы рассмотреть in вариантов, а с использованием метода динамического программирования - всего i×n вариантов. При использовании (1.266) вычисление Вm производится в направлении возрастания аргумента, т.е. в "прямом времени", поэтому уравнение (1.266) называют прямым уравнением Беллмана. Уравнение Беллмана в обратном времени называют обратным уравнением Беллмана. Для получения обратного уравнения Беллмана производят инвариантное погружение исходной задачи в семейство задач:
где При m=1 имеем
Введем функцию Беллмана
Очевидно,
или
В более сложных случаях при выводе уравнения Беллмана используется принцип оптимальности. Принцип оптимальности В общем случае принцип оптимальности формулируется следующим образом: оптимальная стратегия (поведение) обладает тем свойством, что, каковы бы ни были начальное состояние и решения на начальном этапе, решения на последующем этапе должны составлять оптимальную стратегию относительно состояния, которое получается в результате принятия решений на начальном этапе. В задачах оптимального управления оптимальность определяется функционалом (критерием оптимальности) J(u(t),x(t)), состояние -фазовым вектором x(t), стратегия - это управление u(t) на всем интервале [t0, tf], решение - это выбор управления. Для задачи оптимизации справедлив принцип оптимальности, обладающий марковским свойством. По определению, задача оптимального управления обладает марковским свойством, если после выбора управления на интервале [t, t¢] влияние процесса управления (u(t), x(t)) на оставшемся интервале [t¢, tf ] на величину функционала J(u(t),x(t)) зависит только от состояния x ¢(t¢) в конце начального интервала и выбора управления в последующие моменты времени, т.е. на интервале [t', tf]. Для формулировки принципа оптимальности рассмотрим задачу
Для этой задачи справедлив принцип оптимальности, формулируемый следующим образом: для оптимальности допустимой для задачи (1.268) пары (u*(t), x*(t)) необходимо, чтобы при любом t' Î [t0, tf] управление u*[t',tf] было оптимальным относительно состояния x*(t), в котором окажется объект в момент t' при использовании на начальном отрезке времени t0<t<t' управления u*[t0,t']. Этот принцип называют прямым принципом оптимальности. Это утверждение доказывается от противного. Допустим, что утверждение неверно, и существует допустимое управление | ||
|
| Поделиться: |

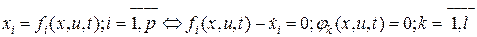 ;
;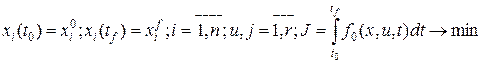 . (1.242)
. (1.242) , (1.243)
, (1.243)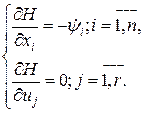 (1.244)
(1.244)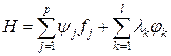 , (1.245)
, (1.245) и уравнения приобретают вид
и уравнения приобретают вид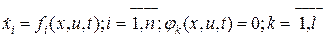 ;
; . (1.247)
. (1.247)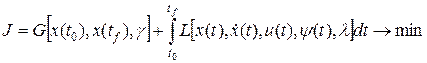 , (1.248)
, (1.248) .
.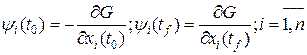 . (1.249)
. (1.249) (1.250)
(1.250)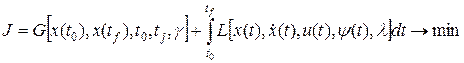 , (1.251)
, (1.251)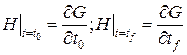 . (1.252)
. (1.252)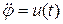 . Найти матрицы А и В, определить управляемость системы. Привести к виду
. Найти матрицы А и В, определить управляемость системы. Привести к виду  .
. так, чтобы
так, чтобы 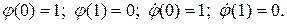

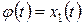 .
.
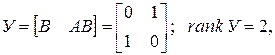

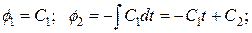
 .
. .
. .
. .
.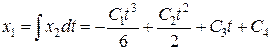 .
.
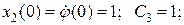
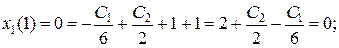
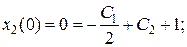

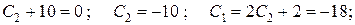
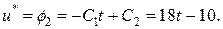


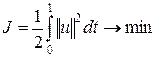 при условии
при условии 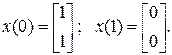
 .
.
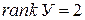 , следовательно, система наблюдаема.
, следовательно, система наблюдаема.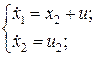
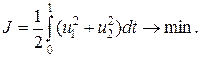
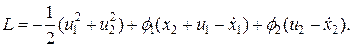

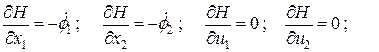
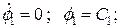
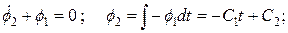
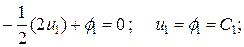
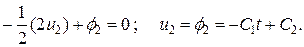
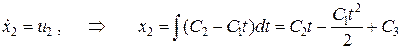 .
.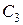

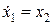 следует
следует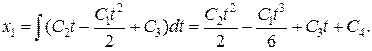
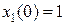 следует
следует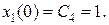
 следует
следует
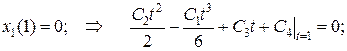
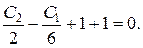
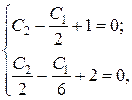
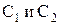
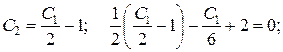

 получим:
получим:


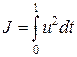 при начальных условиях
при начальных условиях 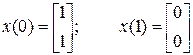 .
.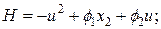

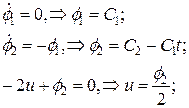


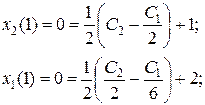
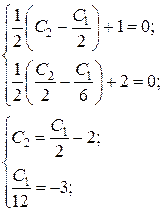
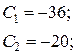
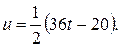
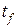
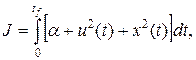

 .
.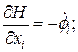
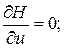
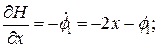
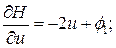


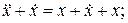
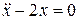 .
.
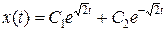 .
.

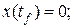
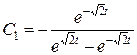 .
.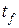 не фиксирован, то необходимо записать условия трансверсальности. Для этого составим функцию G. Так как на начальное и конечное состояние объекта ограничения не наложены, то G=0. Тогда условия трансверсальности примут вид:
не фиксирован, то необходимо записать условия трансверсальности. Для этого составим функцию G. Так как на начальное и конечное состояние объекта ограничения не наложены, то G=0. Тогда условия трансверсальности примут вид: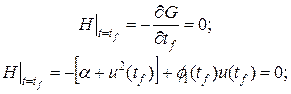
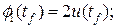


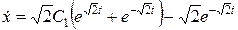 .
.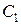 её значение и приводя подобные слагаемые, получим:
её значение и приводя подобные слагаемые, получим: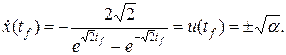
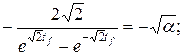
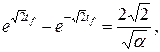
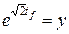
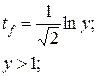
 .
.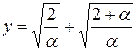 .
. выполним аналогичные операции.
выполним аналогичные операции.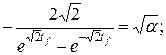
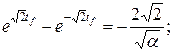



 , тогда
, тогда 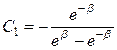 .
.
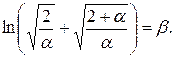

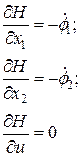
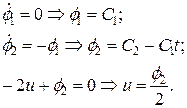
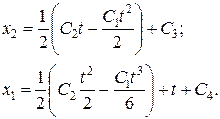

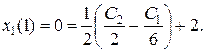
 не закреплена, то необходимо использовать условия трансверсальности. По условию задачи на координату
не закреплена, то необходимо использовать условия трансверсальности. По условию задачи на координату 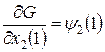 , тогда
, тогда
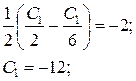

 .
. при
при  . Определить
. Определить 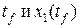 .
.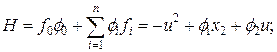
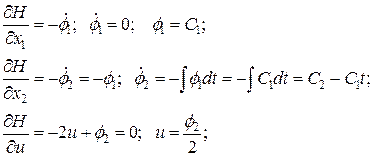


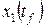 , запишем функцию G:
, запишем функцию G:
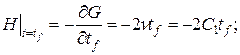




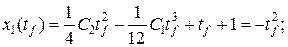

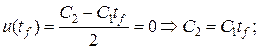




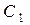 во второе уравнение системы и приведя подобные слагаемые, получим квадратное уравнение относительно
во второе уравнение системы и приведя подобные слагаемые, получим квадратное уравнение относительно  .
.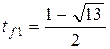 и
и 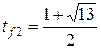 . Так как
. Так как 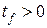 , то условию задачи удовлетворяет второй корень
, то условию задачи удовлетворяет второй корень  .
.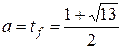 .
.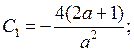


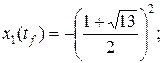

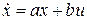 ,
, в фиксированное конечное состояние
в фиксированное конечное состояние 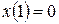 при условии минимума функционала
при условии минимума функционала .
.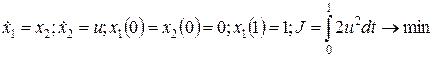 .
.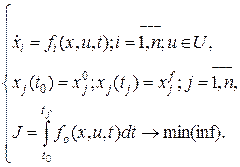 (1.253)
(1.253) , (1.254)
, (1.254) , (1.255)
, (1.255) . (1.256)
. (1.256) ;
; .
.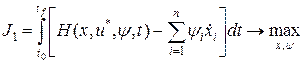 ; (1.257)
; (1.257)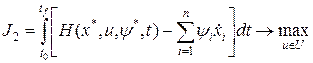 . (1.258)
. (1.258) ; (1.259)
; (1.259) . (1.260)
. (1.260)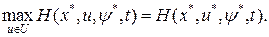 (1.261)
(1.261)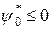 и решение
и решение 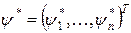 сопряженной системы (1.259) при х (t) =x*(t) и u(t)=u*(t), что при любом t Î [t0, tf], кроме точек разрыва u*(t) функция
сопряженной системы (1.259) при х (t) =x*(t) и u(t)=u*(t), что при любом t Î [t0, tf], кроме точек разрыва u*(t) функция  достигает при u(t)=u*(t) максимума, т.е. выполняется соотношение (1.261).
достигает при u(t)=u*(t) максимума, т.е. выполняется соотношение (1.261).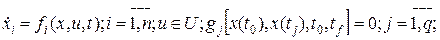
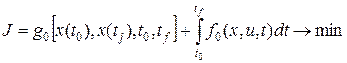 (1.262)
(1.262) непрерывны и непрерывно дифференцируемы. Функции
непрерывны и непрерывно дифференцируемы. Функции 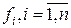 обладают такими же свойствами, что и (1.253).
обладают такими же свойствами, что и (1.253).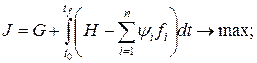
 .
.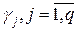 и решения
и решения 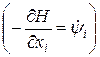 , если фазовое ограничение отсутствует (функция
, если фазовое ограничение отсутствует (функция 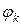 от фазовых координат не зависит). Они не содержат уравнений Эйлера-Лагранжа
от фазовых координат не зависит). Они не содержат уравнений Эйлера-Лагранжа 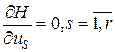 , которые определяют условия стационарности. Вместо них имеется условие максимума. Если ограничения на управление задается метод неопределенных множителей Лагранжа нахождения экстремума функции, из получим недостающие уравнения Эйлера-Лагранжа.
, которые определяют условия стационарности. Вместо них имеется условие максимума. Если ограничения на управление задается метод неопределенных множителей Лагранжа нахождения экстремума функции, из получим недостающие уравнения Эйлера-Лагранжа.
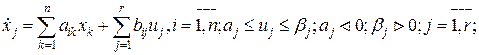
 . (1.263)
. (1.263)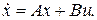
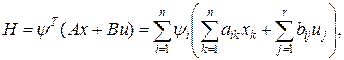
 подчиняется сопряженному уравнению
подчиняется сопряженному уравнению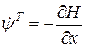 ,
,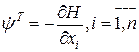 .
.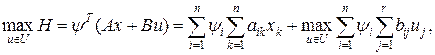
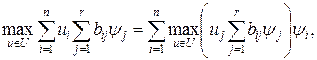
 .
. обращается в нуль только в изолированных точках.
обращается в нуль только в изолированных точках.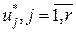 оптимального управления u* кусочно-постоянны и принимают крайние значения aj или bj:
оптимального управления u* кусочно-постоянны и принимают крайние значения aj или bj: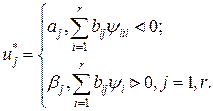

 .
.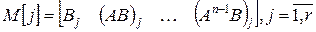 ,где
,где  – j-е столбцы матриц
– j-е столбцы матриц  .
.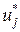 кусочно-постоянны, принимают только крайние значения и имеют не более n интервалов постоянства, т.е не более n-1 переключений.
кусочно-постоянны, принимают только крайние значения и имеют не более n интервалов постоянства, т.е не более n-1 переключений.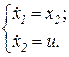
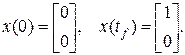 Найти время переключения
Найти время переключения 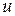 и
и 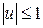 .
.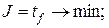
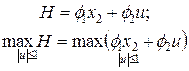 .
.
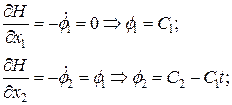
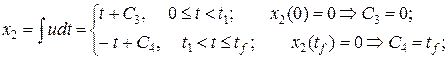
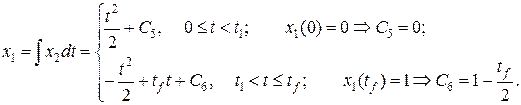
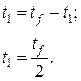

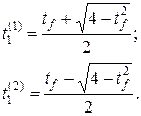
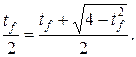
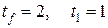 .
.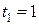 .
. ;
;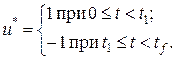
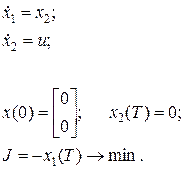
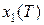 и траектории
и траектории  .
.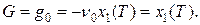
 или
или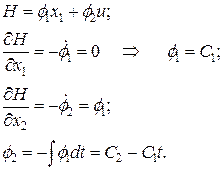
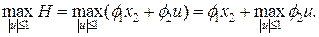


 -момент переключения.
-момент переключения.
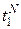
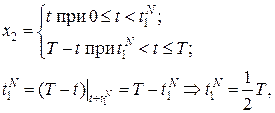

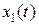


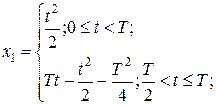
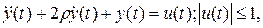
 , (1.264)
, (1.264)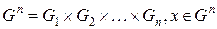 - прямое произведение областей (множеств) определения функций fi (xi). Рассмотрим семейство задач
- прямое произведение областей (множеств) определения функций fi (xi). Рассмотрим семейство задач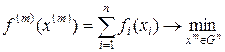 . (1.265)
. (1.265)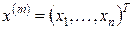 .
.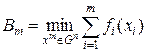 .
. .
.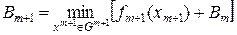 ,
,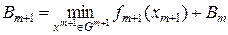 , (1.266)
, (1.266)
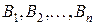 и
и 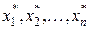 . Решением исходной задачи будут Вn и
. Решением исходной задачи будут Вn и  .
.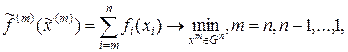

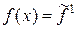 .
.
 ,
,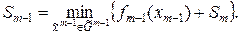 (1.267)
(1.267) (1.268)
(1.268)


