
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы синтеза оптимальных систем управленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 1.4.1.Общие положения
Задача синтеза оптимальной системы состоит в том, чтобы для заданного объекта рассчитать регулятор и программатор, которые в определенном смысле наилучшим образом решают поставленную задачу управления. В соответствии с этим рассматриваются две задачи: - синтез оптимального программатора; - синтез оптимального регулятора. Математически эти задачи могут быть сформулированы единообразно и решаются одними и теми же методами. Но целесообразно их раздельное рассмотрение, так как решение первой задачи - определение программного управления, а второй - управление с обратной связью. Программное управление - это управление в виде функции от времени, управление с обратной связью - управление в виде функции от фазовых координат. Системы с оптимальным программатором называют оптимальными по режиму управления, а системы с оптимальным регулятором - оптимальными по переходному режиму. Система называется оптимальной, если оптимальными являются программатор и регулятор. 1.4.2.Общая постановка задачи оптимального управления Задача синтеза оптимальных систем управления формулируется как вариационная задача. Пусть уравнение объекта задается в нормальной форме
или в скалярном виде
На управление и фазовый вектор могут быть наложены ограничения в виде уравнений связи
или в виде включения в множества
где Ut, Xt, - некоторые заданные множества, зависящие от времени. Причем
т.е. Ut - подмножество r-мерного пространства; Xt - подмножество n-мерного пространства. Краевые (граничные) условия - ограничения на фазовый вектор в начальный t0 и конечный tf моменты времени:
Вектор X(to) называют левым, а вектор X(tf) - правым концом траектории. Критерий оптимальности, являющийся числовым показателем качества системы, задается в виде функционала J=J[u(t),x(t)]. (1.210) Задача оптимального управления формулируется следующим образом: при заданных уравнении объекта управления (1.207), ограничениях (1.208) и краевых условиях (1.209) требуется найти такие программное управление U*{t) или управление с обратной связью U*[X(t),t] и фазовую траекторию X*(t), при которых критерий (1.210) принимает минимальное {или максимальное) значение. Управления U* (t), U*[X(t),t] и траектория X*(t) называются оптимальными. Классификация задач оптимального управления По виду ограничения разделяют задачи оптимального управления: классического типа, когда ограничения задаются в виде равенства
неклассического типа, когда ограничения задаются в виде неравенств
Задачи неклассического типа можно преобразовать к задачам классического типа введением дополнительных переменных. По виду краевых условий различают задачи: - с фиксированными (закрепленными) концами, когда каждое из множеств Xo,Xf состоит из одной точки [X (t0) =X0;X (tf) =Xf;X0,Xf - заданные точки]; - с подвижным правым концом (Xf состоит более, чем из одной точки), с подвижным левым концом (Х0 состоит более, чем из одной точки), с подвижными концами (оба конца подвижны); - со свободным правым концом (Xf совпадает со всем фазовым пространством, т.е. на правый конец никаких ограничений не наложено). По времени начала и окончания процесса различают задачи: - с фиксированным временем, когда начальный t0 и конечный tf моменты времени фиксированы; - с нефиксированным временем, когда один из моментов времени t0 или tf не фиксирован. По критерию оптимальности различают: - задачу Больца; при этом критерий имеет вид
- задачу Лагранжа; при этом критерий имеет вид
- задачу Майера; при этом критерий имеет вид
Задача Майера в частном случае, когда функционал имеет вид J=g0[X(tf),tf] называется задачей терминального управления, когда функционал имеет вид J=[tf-t0] - задачей максимального (оптимального) быстродействия. Путем преобразования переменных можно перейти от одной задачи к другой, в этом смысле они эквивалентны. 1.4.3.Метод классического вариационного исчисления (метод множителей Лагранжа) Понятия вариационного исчисления. Переменная величина J[X(t)] называется функционалом, зависящим от функции X(t), если каждой функции X(t) (из некоторого класса функций) соответствует число J. Аналогично можно определить функционалы, зависящие от нескольких функций. Функционал J[X(t)] достигает на X*{t) минимума, если его значение на любой близкой к X*(t) кривой X(t} не менее, чем J[X*(t)], т.е.
Аналогично определяется кривая, на которой реализуется максимум. В этом случае Введем понятие близости кривых. Кривые X(t) и
где x - достаточно малое число На рис.1.2представлены кривые, близкие в смысле нулевого и первого порядка соответственно.
Рис.2.Кривые близкие в смысле нулевого (а) и первого (б) порядков.
Если функционал J[X(t)] достигает на кривой X* (t) минимума (максимума) по отношению ко всем кривым, близким к X*(t) в смысле близости нулевого порядка, то такой минимум (максимум) называется сильным. Если же этот функционал достигает минимума (максимума) лишь по отношению к кривым, близким к X*(t) в смысле близости 1-го порядка, то такой минимум (максимум) называют слабым. Разность функций Простейшая задача вариационного исчисления. Уравнение Эйлера Исследуем на экстремум функционал
где Искомая функция, для которой J[X(t)] принимает экстремальное значение, удовлетворяет краевым условиям X(t0)=X0; X(tf)=Xf. (1.212) Задача о нахождении экстремума функционала (1.211) при условиях (1.212), в которой X0, Xf - заданные числа, называется вариационной задачей с закрепленными концами. Непрерывно дифференцируемые функции X(t), определенные на [t0,tf] и удовлетворяющие условиям (1.212), называются допустимыми функциями. Допустим, решение этой задачи - X*(t). Тогда возьмем некоторую функцию X(t) и составим параметрическое семейство кривых
где a - некоторое число. Закрепим концы кривых этого семейства в концевых точках: X(t0,a)=X0; X(tf,a)=Xf. (1.214) Подставим выражение (1.213) в функционал (1.211) с учетом определения вариации и ее производной
получим
В связи с нашим предположением, что X*(t) - решение задачи (1.211), (1.212), то J(a) имеет экстремум при a=0, так как X (t,0}=Х*(t). Тогда можно использовать необходимое условие экстремума функции одной переменной:
из которого после подстановки в него (1.216) получим
Используя (1.213) и (1.216) представим это уравнение в виде
После интегрирования по частям 2-го слагаемого с учётом того, что
Используя краевые условия (1.214) и подставляя это выражение в (4.11), получим окончательно
В выражении (1.218) под интегралом стоит произведение вариации 3x(t) r, которая является произвольной величиной на (а, b) и некоторая функция
заданная на функции Тогда в соответствии с основной леммой вариационного исчисления из (1.218) следует, что
которое выполняется на экстремалях X*(t). Действительно, пусть
на отрезке [t1, t2] Î [t0, tf ] и сохраняет на нем знак. Тогда в силу произвольности выбора Итак, мы получили необходимое условие экстремума задачи (1.211), (1.212) в виде уравнения (1.219), которое носит имя Эйлера. В развернутом виде (после дифференцирования по t) это уравнение принимает вид с учетом
Его решения x(t,C1,C2), где C1,C2 - постоянные, определяемые граничными условиями (1.212), называется экстремалями. Если функционал (1.211) содержит
при выполнении граничных условий
Повторяя все действия, выполненные при выводе уравнения Эйлера, нетрудно показать, что экстремум функционала (1.222) является решением уравнения Эйлера-Пуассона:
Решение этого уравнения х(t,C1, C2, С3, С4) содержит постоянные d, которые определяются из граничных условий (1.223). Задача с подвижными концами и нефиксированным временем начала и конца Если концы подвижны, а время зафиксировано, то в этом случае вариационная задача состоит в определении экстремума функционала
Как и ранее, составим параметрическое семейство кривых (1.213), причем концы этих кривых принадлежат кривым X(t0) и X(tf):
Подставляя (1.213) в (1.225) и учитывая (1.215), получим
Используя, как и ранее, необходимые условия экстремума
в котором, интегрируя по частям второе слагаемое под интегралом и используя (2,3) и (1.216), получим
Так как функция x*(t) должна доставлять экстремум при фиксированных х* (t0) и x*(tf), то она должна удовлетворять уравнению Эйлера
а в силу произвольности
которые называются условиями трансверсальности. Если в вариационной задаче оставить свободными также t0, tf, то функционал (1.225) принимает вид
Проделав выкладки как и ранее, но учитывая, что g0 является функцией t0, tf, уравнение (1.228) принимает вид:
В силу независимости вариаций
Уравнение Эйлера-Лагранжа Рассмотрим задачу Эйлера-Лагранжа, состоящую в отыскании экстремума функционала
при условиях
где В отличие от предыдущих задач на аргументы функционала наложены не только краевые условия (1.236), но и дополнительные ограничения (связи (1.235), (1.236)) и они уже не являются независимыми. Для решения задачи (1.234)- (1.237) составим функцию Лагранжа:
где y0, yi, lk- так называемые коэффициенты Лагранжа, причем y0, lk - константы, a yiв общем случае - функция времени (в задачах оптимизации обычно полагают, что y0=-1). Задача (1.234)- (2.27} сводится к решению простейшей вариационной задачи:
Эта задача имеет смысл, если только не все множители y0, yi, lk равны одновременно нулю. В задаче (1.239) роль аргумента играет вектор у=(x, y, l)т и в силу (1.219) уравнения Эйлера для всех составляющих вектора у имеют вид
Можно проверить, что уравнения (1.241) совпадают с (1.235) и (1.236), поэтому для решения задачи (2. 23)-(1.236) достаточно уравнений (1.240), ограничений (1.235), (1.236) и краевых условий (1.237). Уравнения (1.240) называются уравнениями Эйлера-Лагранжа.
|
||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 1164; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

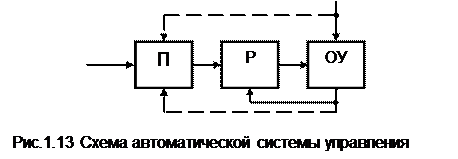
 . (1.207)
. (1.207) ,
, – фазовый вектор;
– фазовый вектор; – вектор управления.
– вектор управления. ,
, , (1.208)
, (1.208) ,
, . (1.209)
. (1.209) ;
; .
. ,
, ,
, .
.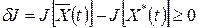 .
. для всех кривых, близких к X*(t).
для всех кривых, близких к X*(t). близки в смысле близости нулевого порядка, если разность
близки в смысле близости нулевого порядка, если разность 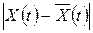 мала. Кривые X(t) и
мала. Кривые X(t) и  близки в смысле 1-го порядка, если малы разности
близки в смысле 1-го порядка, если малы разности  и
и  ,и, наконец, указанные кривые близки в смысле k-го порядка, если
,и, наконец, указанные кривые близки в смысле k-го порядка, если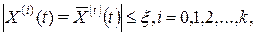
 - производные i-го порядка;
- производные i-го порядка;
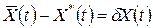 называют вариацией аргумента X(t) функционала J[X(t)].
называют вариацией аргумента X(t) функционала J[X(t)]. , (1.211)
, (1.211) - непрерывная и трижды дифференцируемая функция своих аргументов.
- непрерывная и трижды дифференцируемая функция своих аргументов. , (1.213)
, (1.213)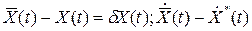 , (1.215)
, (1.215) . (1.216)
. (1.216) ,
, .
.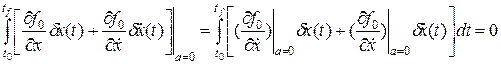 . (1.217)
. (1.217)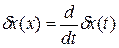 имеем:
имеем: .
. . (1.218)
. (1.218) ,
, , доставляющей экстремум функционалу (1.211).
, доставляющей экстремум функционалу (1.211). , (1.219)
, (1.219)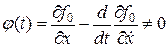 , (1.220)
, (1.220) , а, следовательно и dx(t), выберем dx(t) такую, чтобы она сохраняла знак на [t1, t2] и dх (t) =0 при t Î [t0, t1] и t Î [t2,tf]. Тогда интеграл (1.218) будет отличен от нуля, а, следовательно, предположение (1.220) неверно.
, а, следовательно и dx(t), выберем dx(t) такую, чтобы она сохраняла знак на [t1, t2] и dх (t) =0 при t Î [t0, t1] и t Î [t2,tf]. Тогда интеграл (1.218) будет отличен от нуля, а, следовательно, предположение (1.220) неверно. ,
, . (1.221)
. (1.221)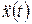 , что встречается в задачах управления, то следует рассмотреть задачу поиска экстремума функционала
, что встречается в задачах управления, то следует рассмотреть задачу поиска экстремума функционала , (1.222)
, (1.222)
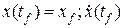 . (1.223)
. (1.223) . (1.224)
. (1.224) . (1.225)
. (1.225) . (1.226)
. (1.226) . (1.227)
. (1.227) и тот факт, что экстремум J достигается на х*(t)=x(t,0), получим уравнение
и тот факт, что экстремум J достигается на х*(t)=x(t,0), получим уравнение ,
, . (1.228)
. (1.228) и
и  и их независимости, то и уравнениям
и их независимости, то и уравнениям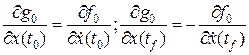 , (1.230)
, (1.230) . (1.231)
. (1.231) (1.232)
(1.232) .
. и из условий оптимальности х*(t) получим условия (1.229), (1.230) и дополнительно к условиям трансверсальности условия
и из условий оптимальности х*(t) получим условия (1.229), (1.230) и дополнительно к условиям трансверсальности условия . (1.233)
. (1.233) , (1.234)
, (1.234) ; (1.235)
; (1.235) ; (1.236)
; (1.236)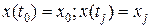 (1.237)
(1.237) все fi,jk - дифференцируемые по своим аргументам функции.
все fi,jk - дифференцируемые по своим аргументам функции.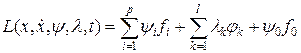 , (1.238)
, (1.238) . (1.239)
. (1.239) , (1.240)
, (1.240) . (1.241)
. (1.241)


