
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы с адаптацией в особых фазовых состоянияхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Недостаток адаптивных систем с контуром самонастройки – сложность реализации вычислительных блоков для определения условий экстремума, снижение надежности функционирования. В отдельных случаях задача адаптации решается более простыми средствами, используя особенности нелинейных систем. В нелинейных системах могут возникать автоколебательные или скользящие режимы, что может быть использовано для получения дополнительной информации об управляемом, процессе либо особый режим преднамеренно организуется, придавая системе свойства адаптации к параметрическим или внешним возмущениям. Рассмотрим два класса таких систем: релейные автоколебательные системы и адаптивные системы с переменной структурой. 2.5.1.Релейные автоколебательные системы управления
В нелинейной системе, состоящей из релейного элемента и линейной части с передаточной функцией W0(p) (рис. 2.8), используя метод гармонической линеаризации, можно определить зависимость параметров автоколебаний от параметров линейной части. Пусть передаточная функция линейной части
где Т1, Т2 – постоянные времени, константы; k0(t) – переменный коэффициент усиления. Уравнение релейного элемента
При g(t) = 0 общее уравнение для оператора нелинейной системы
Гармоническая линеаризация релейного элемента
Поэтому (3) можно записать
откуда при условии p = jw находятся амплитуда и частота автоколебаний:
Таким образом,
Поддерживая амплитуду автоколебаний на заданном уровне, можно создать систему, адаптирующуюся к указанному параметрическому возмущению.
На рис. 9 приведена такая система с регулируемым уровнем ограничения релейного элемента. На основании (2.73) амплитуда автоколебаний может поддерживаться на постоянном уровне при изменениях k0(t) за счет изменения уровня ограничения реле [u0+Du0(t)]. Уравнения системы: релейного элемента
Уравнение фильтра, настроенного на частоту автоколебаний a0 yф = kфpy(t). (2.75) Уравнение двухполупериодного выпрямителя сигнала автоколебаний za = |yф|. (2.76) Уравнение исполнительного устройства для перестройки уровня ограничения релейного элемента
где Уравнение основного контура
После гармонической линеаризации (2.78) получим
откуда параметры автоколебаний
Пусть экстремальный режим определяется следующими значениями: a = a0; k0(t) = k0; Du0(t) = 0; Dz = 0, (2.81) тогда можно определить значение опорного напряжения z(a0):
Линеаризация (2.82) по постоянной составляющей даст z(a0) = 2kфa0w0/p. (2.83) Учитывая (2.80) и (2.81), получим
При изменении коэффициента k0(t) будут изменяться амплитуда автоколебаний и среднее выпрямленное напряжение za. Появляющееся рассогласование Dz=z(a0)-za, будет воздействовать на изменение уровня ограничения релейного элемента Du0(t) таким образом, чтобы уменьшалась до нуля величина Dz. 2.5.2.Адаптивные системы с переменной структурой В системах с переменной структурой за счет нелинейного сочетания различных линейных структур удается организовать специфическое вынужденное движение – скользящий режим – режим перехода от движения, соответствующего одной линейной структуре, к движению, соответствующему другой линейной структуре. Этот переход осуществляется логическим переключателем связей в системе в зависимости от ее фазового состояния. Такой переход осуществляется с большой частотой, в пределе стремящейся к бесконечности. После возникновения скользящего режима движение системы происходит вдоль границы переключения и становится независимым от параметров управляемого объекта. Поэтому переменные параметры объекта не оказывают влияния на динамические свойства системы с переменной структурой, находящейся в скользящем режиме. Пусть система с переменной структурой описывается дифференциальными уравнениями
где xi – фазовые координаты; ai(t) – переменные параметры системы; u – управление. Известны диапазоны изменения параметров:
Управление выбирают в следующем виде:
где yi – коэффициенты, являющиеся разрывными функциями фазового состояния системы
Гиперповерхность g=0 является поверхностью разрыва коэффициентов yi, т.е. вдоль этой поверхности происходит движение в скользящем режиме. Так как уравнение движения по поверхности g=0 зависит только от постоянных коэффициентов ci, выбираемых из условия обеспечения требуемого качества переходных процессов, то движение в скользящем режиме не зависит от переменных параметров ai(t).
Для обеспечения скользящего режима необходимо выбирать значения постоянных коэффициентов ai и bi в соответствии с условием gdg/dt < 0 или неравенствами
При постоянных значениях ai и bi условия (22) накладывают ограничения на выбор коэффициентов поверхности скольжения сi из допустимой области  при изменениях параметров ai(t) в заданном диапазоне при изменениях параметров ai(t) в заданном диапазоне 
На рис. 2.10 для двумерного случая заштрихована область изменения коэффициентов поверхности скольжения ci, полученная из условий обеспечения скользящего режима. При этом cmax выбирают из условий (2.89), а cmin – из условия максимальной заданной длительности переходного процесса tmax. Если в экстремальном режиме функционирования системы необходимо поддерживать максимальное быстродействие в переходных процессах, то в процессе изменения параметров объекта ai(t) необходимо определять значение cmax и перестраивать коэффициенты поверхности скольжения при их несоответствии этому значению. Такая задача может быть решена адаптивной системой с переменной структурой, использующей информацию о наличии скользящего режима в системе. Принцип действия такой адаптивной системы заключается в следующем. В начале переходного процесса в регуляторе формируется функция переключения g0 = cminx1+x2, (2.90) где cmin – определяется либо из максимальной заданной длительности переходного процесса, либо из условия (2.89) при минимальных значениях ai(t) из диапазона На поверхности g0 (в данном случае прямая) возникает скользящий режим при любых значениях ai(t) из заданного диапазона. Факт возникновения скользящего режима регистрируется индикатором, выходной сигнал которого скачкообразно изменяется при уменьшении относительной длительности пребывания системы в состоянии одной из имеющихся структур, т.е. при повторных изменениях знака функции g0. По сигналу индикатора скользящего режима функция переключения перестраивается с g0 на g1: g1 = (cmin+Dc)x1+x2. (2.91) В системе вновь возникает скользящий режим, но уже на линии переключения g1=0. С помощью индикатора скользящего режима происходит дальнейшее перестроение функции переключения gi = (cmin+iDc)x1+x2, (2.92) до тех пор, пока значение коэффициента (cmin+iDc) не превысит значение Сmax, после чего скользящий режим по условию (2.89) возникнуть не сможет, и перестроение функции переключения закончится. Движение фазовой точки после того момента будет происходить по близкой к границе gmax=cmaxx1+x2=0 фазовой траектории одной из структур без скользящего режима (рис. 2.11). Шаг приращения Dс должен выбираться в зависимости от допустимого перерегулирования h в переходном процессе. Таким образом, за счет предельного по условию (2.89) режима работы поддерживается максимальное быстродействие системы управления при изменении параметров объекта.
2.5.3.Пример адаптивной системы управления с переменной структурой В большинстве случаев к СУ предъявляются порой противоречивые требования: максимального быстродействия в случае аварийных ситуаций и максимальной точности в нормальных режимах работы. В таких случаях используют нелинейные алгоритмы управления, которые при малых отклонениях выходной координаты являются линейными, обеспечивающими высокую точность управления, а в аварийных режимах – приближаются к релейным, обеспечивая быстрое изменение выходной координаты объекта.
Существует множество разновидностей таких алгоритмов, которые в общем виде можно представить в такой форме
где e – ошибка регулирования; Т – постоянная времени интегрирующего звена; F1(e), F2(e) – нелинейные функции от e. В качестве Fі(e) можно использовать следующие: F(e) = e2sign e; F(e) = ae3; (2.94) F(e) = ae5 и т.д., где а – константа. При этом на управляющее воздействие наложены ограничения
где Jmin, Jmax – минимальное и максимальное значения управления J(t).
На рис. 2.12 приведена функциональная схема нелинейного адаптивного регулятора с идентификацией коэффициента усиления объекта (см. рис. 2.7) и переменной структурой. 2.5.4.Контрольные вопросы и упражнения 1. Каковы преимущества релейных автоколебательных систем и систем с переменной структурой по сравнению с самонастраивающимися системами? 2. Покажите зависимость амплитуды автоколебаний релейной системы от характеристик релейного элемента и параметров линейной части системы. 3. Приведите структурную схему адаптивной релейной системы управления. 4. В чем заключается сущность скользящего режима системы управления? 5. Каковы необходимые условия существования скользящего режима. 6. В чем заключается принцип действия адаптивной системы в скользящем режиме? 7. Приведите пример адаптивной системы управления. Обучающиеся системы Обучающиеся системы создаются на основе принципа обучения, заключающегося в постепенном накоплении опыта формирования поведения системы при высокой степени неопределенности ее исходных состояний, по результатам которого происходит улучшение функционирования системы. Способы накопления опыта могут быть разные, однако у всех есть общая черта – постепенное выделение «области знаний» из всей совокупности незнания. Это нашло отражение в использовании методов распознавания образов (классификации). Под классификацией понимается установление по результатам накопленного опыта границ между определенными классами сложных ситуаций. Задача автоматического обучения классификации формулируется следующим образом. Каждой возможной ситуации из множества рассматриваемых ставится в соответствие точка некоторого пространства х. Заранее известно, что в пространстве х необходимо выделить две или большее число областей или классов ситуаций.
Существует два подхода к обучению такому разделению: 1) обучение с поощрением, когда к классифицирующему автомату предъявляют ряд случайных точек из множества в пространстве х и сообщают информацию о принадлежности этих точек определенным классам. После цикла обучения автомат строит разделяющую поверхность и в дальнейшем может отличать принадлежность разным классам любых точек в пространстве х; 2) обучение без поощрения, когда автомат определяет факт компактного расположения нескольких точек по наблюдениям и строит разделяющие поверхности на основе меры близости компактных групп точек к разделяющей поверхности. Сложность обучения заключается в том, что не всегда классы из близко расположенных друг к другу точек строго отделимы, т.е. возможно пересечение классов. 2.6.1.Метод секущих плоскостей Пусть требуется разделить три фигуры, состоящие из набора точек. В автомат вводят сначала значения двух точек 1 и 2 (рис. 2.13). Автомат запоминает их и строит произвольную плоскость, разделяющие эти точки (точка 2 принадлежит классу В). После предъявления точки 3 эта точка оказывается выше плоскости I и, следовательно, должна быть отнесена к классу В. Однако известно, что эта точка из класса А. Противоречие разрешается построением новой плоскости II. При появлении новых точек 4 и 5 противоречий не возникает, и автомат не проводит новых плоскостей. При появлении точки 6 возникает противоречие между этой точкой, принадлежащей классу В и точками 4 и 5. Тогда сначала строят плоскость III, разделяющую точки 1 и 6, а затем плоскость IV, разделяющую точки 5 и 6. Постепенно области, где точки противоречат разделению, сужаются и вероятность возникновения противоречий уменьшается. После цикла обучения построению разделяющих поверхностей можно отбросить лишние участки и получить разделяющую поверхность, состоящую из нескольких гиперплоскостей. 2.6.2.Метод потенциальных функций Обычно задача обучения классификации рассматривается как задача разделения на два класса: Q и R. В детерминированной постановке оба класса не пересекаются друг с другом и могут быть четко отделены друг от друга. Метод потенциальных функций позволяет за конечное число показов входных сигналов из обучающей последовательности построить разделяющую функцию Ф(х), принимающую положительные значения в точках, соответствующих классу Q и отрицательное в точках, соответствующих классу R. Ф(х) в N-мерном пространстве признаков должна быть ограничена и представима линейной комбинацией ограниченных на х функций
где ci – неизвестные коэффициенты, обеспечивающие «достаточную гладкость» Ф(х); ji –система функций разложения. Причем должно соблюдаться условие
где li – последовательность положительных чисел, для которой
Каждой входной ситуации
Ввиду ограниченности линейно независимой системы функций ji(х) функция При появлении точек из обучающейся последовательности х1, х2, …, хк строится потенциальная функция для каждой точки. Для первой точки х1
Для второй точки х2
При невыполнении (2.99) k2(x) получается из k1(x) добавлением со знаком множества Q или R (по принадлежности х2) потенциала k(x1,x2). На n-м шаге обучения строится потенциальная функция
где xs,xq – значения, подстановка которых в предшествующий потенциал приводила к ошибке. На (n+1)-м шаге обучения возможны следующие сочетания:
При совпадении знаков множества Q или R (по принадлежности xn+1) и функции kn(xn+1)
При несовпадении знаков необходимо исправление kn(x):
где k(x,xn+1) имеет знак «+» в (2.102) для n = 3 и знак «–» в (2.102) для n = 4. Таким образом, алгоритм построения разделяющей функции можно записать в следующем виде
Алгоритм (2.105) обеспечивает конечное число исправлений ошибок, если функция Ф(х) строго разделяет множества Q и R и представима разложением (2.96). Число исправлений в этом случае не превышает k, т.е.
На основании (2.106) следующий вывод об уменьшении числа исправлений k при прочих равных условиях с увеличением 2.6.3.Вероятностные алгоритмы обучения Трудноразделимые классы ситуаций требуют при автоматической классификации и распознавании образов вероятностных методов. При этом существенное значение приобретают априорные сведения о вероятностных характеристиках принадлежности объектов к тем или иным классам. Если априорные сведения достаточно полны, тогда можно использовать классический байесовский подход теории статистических решений, основанные на минимизации функции среднего риска R:
где х – предъявляемые для классификации ситуации; Х – пространство ситуаций с классами Хk, Xm; Pk – априорная вероятность ситуации в Хk; Fkm – функция потерь, характеризующая ошибочность отнесения ситуации класса Хk к классу Xm, M – число неизвестных заранее классов, причем функция потерь Fkm в классическом подходе выбирается либо постоянной, либо ее можно представить в виде
pk(x) – условная плотность распределения ситуаций класса Xk. Границы между классами Хk и Xm определяются с помощью характеристических функций вида
также зависящих от вектора параметров Подставляя (2.108), (2.109) в (2.107), получим параметрическую форму записи функции среднего риска R(c):
Учитывая, что в (2.110) средний риск R(
Второе слагаемое в (2.111) определяет чувствительность характеристических функций
по знаку которой можно определить принадлежность ситуаций х к классу Xl или Xm (соответственно при Результатом решения уравнения (2.111) является экстремальное значение вектора параметров
или в виде дифференциальных уравнений в случае непрерывных c(t)
где Г[n], Г(t) – квадратные матрицы, определяющие шаг итерации и сходимости значений вектора В случае разделения пространства ситуаций Х только на два класса Х1 и Х2 средний риск R(
Необходимые условия минимума среднего риска
Отсюда разделяющая функция
Правило решения об отнесении ситуаций к классам выглядит так: если если В классическом подходе используются постоянные функции потерь F11, F12, F21, F22 в виде
поэтому разделяющую функцию
или
где
Следовательно, правило классификации (2.118) можно теперь представить таким образом:
Итак классическое байесовское правило классификации заключается в вычислении отношения правдоподобия l(x) и сравнении его с фиксированным порогом h, который зависит от выбранного правила оценки априорных вероятностей P1 и Р2. Нетрудно видеть, что отсутствие априорной информации об отношении правдоподобия лишает возможности использовать классический подход в задачах классификации и распознавания образов. В таких случаях используют методы обучения. 2.6.4.Обучение с поощрением Пусть разделяющая функция имеет вид
На этапах обучения сообщается информация о принадлежности ситуаций х к классам
Поощрение правильного распознавания или его ошибочность определяется в соответствии с неравенствами
и функцией штрафа в виде выпуклой функции разности у и
Учитывая, что разделяющая функция
тогда функция штрафа
Подставив ее в выражение среднего риска R из (2.115), получим
где P(x) = P1p1(x) + P2p2(x) – совместная плотность распределения В соответствии с условием среднего риска
определяются итеративные алгоритмы обучения в дискретном виде
и в непрерывном виде
Если вместо функции штрафа (2.126) взять выпуклую функцию J(c) в виде среднеквадратической ошибки аппроксимации разделяющей функции с помощью
то минимизацию J(c) можно осуществить в соответствии с условием
или
Обозначив
Учитывая, что
откуда можно получить дискретные алгоритмы:
если
если Таким образом, неизвестная разделяющая функция 2.6.5.Самообучение В отличие от обучения с поощрением самообучение происходит только по предъявляемым ситуациям без дополнительной информации о принадлежности ситуации к определенному классу. Теперь система должна автоматически определять не только принадлежность ситуации к классам, но и количество классов, которое, очевидно, не должно быть равно числу предъявленных ситуаций, а меньше его. Информация о количестве классов может быть получена из выражения совместной плотности распределения
входящей в формулу среднего риска
где
По числу максимумов М совместной плотности распределения р(х) определяется число классов, поэтому при самообучении задача заключается в восстановлении совместной плотности распределения р(х) путем ее аппроксимации в виде
где j(х) – выбранная вектор-функция с ортонормированными компонентами;
В результате минимизации функционала
получаем в дискретном виде алгоритм определения ат:
Минимизируя средний риск (2.139), можно получить разделяющую функцию fkm. Например, для случая двух максимумов М=2 (классов) средний риск
Условия минимума R:
где Разделяющая функция имеет вид
Отсюда дискретные алгоритмы самообучения
если
если где Г1 и Г2 – матрицы коэффициентов, определяющие сходимость вектора 2.6.6.Персептронная модель автоматической классификации Рассмотрим принцип действия персептрона МАРК-1 (рис. 2.14). В качестве воспринимающего устройства в персептроне использовано поле рецепторов в виде фотоэлектрического устройства, состоящего из нескольких сотен фотоэлементов. Каждый фотоэлемент может находиться в одном из двух состояний: 0 и 1. Выходные сигналы фотоэлементов поступают на входы «ассоциативных элементов» А, число которых сравнимо с числом фотоэлементов. Каждый А-элемент имеет несколько входов и один выход. Входы А-элементов соединяются с выходами фотоэлементов случайным образом и со случайными знаками. В процессе обучения случайные связи сохраняются неизменными. А-элементы осуществляют алгебраическое суммирование поданных на их входы сигналов с фотоэлементов и сравнивают получаемую сумму с постоянным числом Q в соответствии с алгоритмом
где
Выходные сигналы А-элементов после переключения на независимые переменные коэффициенты lj складываются
и поступают на вход регулирующего элемента R, который может находиться в одном из двух состояний: 0 или 1 в зависимости от положительности суммы (2.148), т.е.
В процессе обучения персептрон должен выдавать выходной сигнал 0 при предъявлении объектов класса А и выдавать 1 при предъявлении объектов класса В. Обучение заключается в том, что коэффициенты lj при каждом показе объектов класса А и получении на выходе А-элементов сигналов 1 увеличиваются на некоторую величину, а при показе объектов класса В уменьшаются на эту величину. Постепенно правильность ответов на предъявляемые объекты увеличивается, так как повышается сумма (2.148) при правильной классификации. По окончании обучения на последовательности объектов конечной длины автомат распознает с определенной точностью объекты классов А и В, если они и не предъявлялись ему на этапе обучения. Решающее правило имеет вид:
Значение коэффициентов li изменяются в соответствии с правилом обучения:
2.6.7.Примеры адаптивных систем управления с использованием метода самообучения Идентификация вероятностных характеристик возмущающих воздействий Возмущающие воздействия объектов управления имеют стохастический характер и зачастую плотности распределения имеют сложный характер, отличающийся от гауссовского распределения. Используя изложенный выше алгоритм классификации, можно определить центры классов, их дисперсии и вероятности. Рассмотрим случай двух классов. Условия минимума среднего риска имеют следующий вид:
где uk – центр k-го класса. Разделяющая функция
Условие (2.152) определяет оптимальные значения параметров смеси Решение уравнений (2.152), (2.153) для случая двух классов приводит к следующим выражениям:
если
если где gi(t) – коэффициент, удовлетворяющий следующим условиям:
Тогда при четной функции потерь разделяющая линия определяется равенством:
а решающее правило имеет вид:
Дисперсия определяется следующим образом:
где При квадратичной функции потерь минимизируется дисперсия, поэтому центры классов u1, u2 определяются по формулам:
2.6.8.Адаптивное управление объектами при контролируемых возмущающих воздействиях В большинстве промышленных объектов возмущающие воздействия представляют собой смеси двух классов. Если идентифицировать вероятностные характеристики возмущающих воздействий, можно использовать их для адаптации управляющего воздействия. Рассмотрим случай аддитивной помехи. В зависимости от того, какие вероятностные характеристики возмущающего воздействия определяются, изменяется и алгоритм управляющего устройства. Если идентифицируются только оценки центров классов возмущающего воздействия, то алгоритм имеет вид
где m1, m2 – коэффициенты усиления объекта соответственно по управляющему и возмущающему входам; q1(t) – вероятность появления управляющего воздействия u1(t). y* – задание. Если алгоритм изучения предусматривает вычисление вероятности появления классов в смеси
где p1(t) – текущее значение вероятности появления первого класса в смеси; q2(t) – неизвестный параметр. В случае вычисления вероятности появления классов в смеси в управляющем устройстве управляющее воздействие определяется по формуле
где Ниже приведены структурные схемы СУ в соответствии с полученными алгоритмами. Алгоритм (2.156) определяет случайную, (2.157) – смешанную и (2.158) – регулярную стратегии управления. СУ со случайной стратегией применяют в случаях, когда возмущающие воздействия сравнительно медленно меняются во времени, а объект имеет стационарные параметры. Возмущающие воздействия полностью контролируемые.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 634; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.73.117 (0.017 с.) |


 (2.68)
(2.68) (2.69)
(2.69) (2.70)
(2.70) (2.71)
(2.71) (2.72)
(2.72)
 (2.73)
(2.73)

 . (2.74)
. (2.74) (2.77)
(2.77)
 (2.78)
(2.78) (2.79)
(2.79)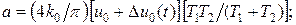 (2.80)
(2.80) .
. (2.82)
(2.82) (2.84)
(2.84) (2.85)
(2.85) . (2.86)
. (2.86) (2.87)
(2.87) (2.88)
(2.88) – постоянные величины.
– постоянные величины. (2.89)
(2.89)

 (2.93)
(2.93) (2.95)
(2.95)
 Расположение границ между областями неизвестно, и нет определения правил, по которым можно определить принадлежность той или иной точки любой из заданных областей. Цель обучения заключается в построении поверхности, разделяющей предъявленные точки из указанного множества на заданное число классов.
Расположение границ между областями неизвестно, и нет определения правил, по которым можно определить принадлежность той или иной точки любой из заданных областей. Цель обучения заключается в построении поверхности, разделяющей предъявленные точки из указанного множества на заданное число классов. (2.96)
(2.96) (2.97)
(2.97)
 в пространстве Х ставится в соответствие потенциальная функция двух переменных:
в пространстве Х ставится в соответствие потенциальная функция двух переменных: . (2.98)
. (2.98) ограничена по модулю при
ограничена по модулю при 
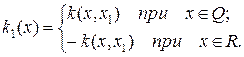 (2.99)
(2.99) (2.100)
(2.100) (2.101)
(2.101) (2.102)
(2.102) (2.103)
(2.103) (2.104)
(2.104) (2.105)
(2.105) (2.106)
(2.106) , т.е. чем более компактны разделяющие множества, тем меньше требуется исправлений ошибок для полного разделения множеств.
, т.е. чем более компактны разделяющие множества, тем меньше требуется исправлений ошибок для полного разделения множеств. (2.107)
(2.107)
 (2.108)
(2.108) – фиксированный вектор параметров;
– фиксированный вектор параметров; (2.109)
(2.109) . (2.110)
. (2.110) (2.111)
(2.111) и граничную или разделяющую любые классы xl и xm функцию
и граничную или разделяющую любые классы xl и xm функцию (2.112)
(2.112) или
или  ).
). , (2.113)
, (2.113) (2.114)
(2.114) (2.115)
(2.115) . (2.116)
. (2.116) получает следующий вид:
получает следующий вид: . (2.117)
. (2.117) то
то  ;
; то
то  . (2.118)
. (2.118)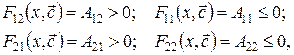 (2.119)
(2.119) можно записать иначе:
можно записать иначе: (2.120)
(2.120) (2.121)
(2.121) – отношение правдоподобия l(x);
– отношение правдоподобия l(x); – фиксированный порог h.
– фиксированный порог h. (2.122)
(2.122) . (2.123)
. (2.123) и
и  :
:
 – правильное распознавание;
– правильное распознавание; – неправильное распознавание
– неправильное распознавание
 (2.124)
(2.124)
 (2.125)
(2.125) принимает вид
принимает вид (2.126)
(2.126) (2.127)
(2.127) , (2.128)
, (2.128) , (2.129)
, (2.129) (2.130)
(2.130) , т.е.
, т.е. (2.131)
(2.131) , (2.132)
, (2.132) (2.133)
(2.133) , получим
, получим (2.134)
(2.134) получим
получим (2.135)
(2.135) (2.136)
(2.136) (2.137)
(2.137) (2.138)
(2.138) (2.139)
(2.139) – функция потерь;
– функция потерь; (2.140)
(2.140) – неизвестные коэффициенты.
– неизвестные коэффициенты. , (2.141)
, (2.141) (2.142)
(2.142) (2.143)
(2.143) (2.144)
(2.144)


 (2.145)
(2.145) и
и (2.146)
(2.146)
 (2.147)
(2.147)


 , (2.148)
, (2.148) (2.149)
(2.149)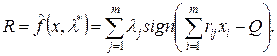 (2.150)
(2.150) (2.151)
(2.151) (2.152)
(2.152) (2.153)
(2.153) , характеризующие центры классов.
, характеризующие центры классов. (2.154)
(2.154)
 (2.155)
(2.155)


 .
.
 при
при 
 при
при 

 – дисперсия класса.
– дисперсия класса.


 (2.156)
(2.156) и
и  , управляющее воздействие для случая двух классов имеет вид
, управляющее воздействие для случая двух классов имеет вид (2.157)
(2.157) (2.158)
(2.158) – заданная вероятность.
– заданная вероятность.



