
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модели динамики в пространстве состоянийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для описания динамики стационарных систем в классической теории управления используются дифференциальные уравнения вида:
где y, U- выходные и входные переменные соответственно. Другой формой описания системы управления является использование передаточных функций
где Y(s),U(s) - изображения по Лапласу выходной и входной координаты соответственно. Однако поведение системы во времени характеризуется не только выходными величинами, но и выходными величинами всех составляющих систем элементов. Комплекс таких величин, полностью характеризующих состояние, порождает пространство состояний системы, т.е. характеризует поведение во времени всех динамических элементов, составляющих систему. Пространством состояний называется метрическое пространство, каждый элемент которого полностью определяет состояние рассматриваемой системы. Состояние понимается в данный момент времени, т.е. как мгновенное состояние. В большинстве случаев достаточно использовать евклидово пространство состояний с евклидовой метрикой. Метрическим пространством называется множество X, в котором задано расстояние между каждыми двумя элементами xÎX и yÎY в виде действительной функции r(x,y), удовлетворяющей трем аксиомам: 1. r(x,y)=0 тогда и только тогда, когда x=y; 2. r(x,y)=r(y,x) (аксиома симметрии); 3. r(x,z)£r(x,y)+r(y,z) (аксиома треугольника). Пусть n - порядок системы, равный числу динамических элементов, тогда движение системы характеризуется траекторией движения n – мерного вектора в пространстве Примерами таких элементов могут служить электрическая цепь с индуктивностью и омическим сопротивлением, механическая система с массой и сопротивлением в виде вязких сил трения и др. При этом дифференциальные уравнения системы представляются в нормальной форме Коши. Если возмущающие воздействия являются детерминированными, то систему можно представить в виде известных функций времени и уравнение указанной системы записать в виде
где В более сложном и общем случае рассматриваемая область пространства состояний разделена на подобласти, для каждой из которых задана своя непрерывная функция, удовлетворяющая указанному условию в области определения. Поведение системы на границах подобластей доопределяется, т.е. определяется дополнительными условиями, например, условиями непрерывности. Если система описывается уравнением (1.3), то процесс в этой системе описывается решением уравнения (1.3) при определенном начальном условии Таким образом, системой в нормальной форме Коши называют систему дифференциальных уравнений первого порядка, разрешенных относительно производных. В общем случае стационарную систему, описываемую линейными дифференциальными уравнениями, можно представить в виде
где
В матричной форме указанную систему записывают в следующем виде
Матрицы-столбцы Вектор F называют вектором возмущения или просто возмущением, а его j-ая координата - j-м возмущающим воздействием. Таким образом, движение системы, описываемой уравнением n–го порядка, характеризуется траекторией движения n - мерного вектора в пространстве Для нестационарных систем уравнение состояния содержит матрицы как функции времени
При наличии аддитивного белого шума уравнение состояния имеет вид
где V0(t) - случайный процесс в виде белого шума:
Q0(t) - матричная функция времени, называемая матрицей интенсивностей. В случае Q0=const она называется матрицей спектральных плотностей белого шума. 1.1.2.Примеры вывода уравнений состояния Уравнение состояния электродвигателя манипулятора Рассмотрим электродвигатель постоянного тока, используемый в качестве исполнительного элемента в манипуляторах. Уравнение электрической цепи:
где U - напряжение сети; eg - ЭДС электродвигателя, i я - ток якоря, Lя - индуктивность якоря. Уравнение механической цепи:
где Mc - момент сопротивления, J - момент инерции, W - угловая скорость вращения электродвигателя, b - коэффициент. Момент электродвигателя:
где Km - коэффициент. ЭДС электродвигателя:
где Ke - коэффициент. После подстановки (1.11-1.13) в (1.9) и (1.10) получим:
Из (1.14) и (1.15) следует:
где Уравнение состояния электродвигателя:
Если обозначить
получим
где
Структурная схема электродвигателя приведена на рис. 1.1. Уравнение движения манипулятора
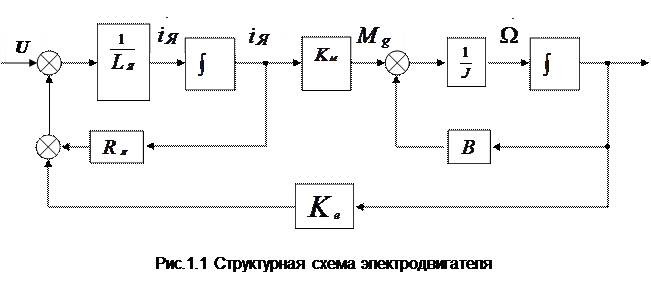
Пусть задан манипулятор с цилиндрической рабочей зоной (рис.1.2). Для вывода уравнения воспользуемся уравнениями Лагранжа второго рода:
гдеi Qi - обобщенные силы, Ek, En - кинетическая и потенциальная энергии системы. Рассмотрим три основные степени подвижности по координатам r,j,z. Размеры ориентирующего узла и объекта в схвате считаем существенно малыми по сравнению с остальными линейными размерами манипулятора. Тогда ориентирующий узел можно представить как твердое тело, что существенно упрощает задачу. Считаем все элементы абсолютно твердыми телами. Рука считается однородным стержнем длиной l и массой m1. Схват с грузом представляет собой точечную массу m. Масса частей, участвующих только в поступательном движении по координатам z и во вращательном движении по координатам j, равна m2. Соответствующий момент инерции, приведенный к вертикальной оси, равен J. Приведенный момент инерции частей, участвующих во вращательном движении, равен J1. Вращающиеся части приводов по координатам r и z учитываются дополнительными приведенными массами Кинетическая энергия манипулятора представляет сумму кинетических энергий отдельных частей.
Потенциальная энергия
где Выбирая обобщенные координаты g1=r, g2=j, g3=z и производя необходимые преобразования в соответствии с (1.19),получим уравнение движения в матричной форме:
где
Fr, Fz – силы, развиваемые приводами по координатам r и z, M - момент, развиваемый приводом по координате j. Уравнение состояния интегро-диффенцирующего звена
Принципиальная схема приведена на рис 1.3.а
В качестве переменных состояния выбираем напряжение на конденсаторах, характеризующее накопленное количество электричества. Получим
Так как
то после подстановки и соответствующих преобразований получим такое уравнение состояния:
Выходная величина y=U2=U1-UC1. Структурная схема приведена на рис 1.3б. Уравнение состояния смесительного бака
Уравнение баланса масс для бака имеет вид:
Мгновенный расход выходного потока F(t) зависит от высоты жидкости h:
где k - константа. При постоянной площади сечения бака S
Тогда уравнения баланса примут вид:
Установившееся состояние при F10=const, F20=const, F0=const, V0=const, C0=const:
При небольших отклонениях от установившегося состояния:
где m1, m2 - рассматриваются как входные переменные, а x1, x2 - переменные состояния. Линеаризация (1.24) и (1.25) приводит к уравнениям
Введем параметр - время заполнения бака:
Исключив x(t) из (1.27), получим линеаризованное дифференциальное уравнение:
где
Если определить выходные переменные в виде:
то уравнение (1.29) можно дополнить линеаризованным уравнением выходной переменной
где 1.1.3.Общее решение дифференциальных уравнений Решение дифференциальных уравнений в матричной форме выполняется с использованием фундаментальной матрицы. Уравнение (1.5) называется неоднородным. Однородное уравнение имеет вид
Пусть Любую такую систему называют фундаментальной системой решений уравнения (1.30). Матрица, составленная из этой системы решений, называется фундаментальной матрицей уравнений (1.6) и (1.30):
Если при t=t0 фундаментальная матрица обращается в единичную, то она называется нормированной. Используя произвольную фундаментальную матрицу Ф(t),нормированную матрицу X(t,t0) можно представить в виде:
где Е - единичная матрица. Нормированная фундаментальная матрица обладает следующими свойствами:
Рассмотрим методику решения дифференциальных уравнений в матричной форме. Пусть динамика системы описывается уравнением в скалярной форме:
где x - неизвестный скаляр, а - константа. Решение этого уравнения известно:
Разложение (1.33) в ряд Тейлора приводит к следующему выражению
Для определения характеристического уравнения системы (1.32) используются преобразование Лапласа уравнения (1.32):
где p - оператор Лапласа. По аналогии с рассмотренным случаем находят характеристическое уравнение системы при векторных переменных. Допустим, в однородном матричном уравнении начальные условия имеют вид X(0)=E. Разложим X(t) в ряд Тейлора в окрестности X(0):
Очевидно С учетом (1.15) получим
Следовательно, решение однородного уравнения (1.6) имеет вид:
Характеристическое уравнение получим путем преобразования по Лапласу (1.38).
откуда характеристическое уравнение:
С помощью нормированной фундаментальной матрицы решение неоднородного уравнения (1.5) при всех t и X(t0)=X0 можно представить в виде соотношения
которое называется формулой Коши. Если матрица А постоянная, то матрица X(t,t0) зависит только от разности (t-t0) и имеет вид
Матричная функция
Уравнение, сопряженное с (1.30), имеет вид:
Если Z(t,t0) – нормированная фундаментальная матрица этого уравнения, т.е.
При решении задач оптимального управления удобно пользоваться также операторным методом решения систем дифференциальных уравнений. Этот метод состоит в том, что посредством интегрального преобразования Лапласа от дифференциального уравнения переходят к вспомогательному алгебраическому уравнению. Затем находят решение преобразованного уравнения, после чего при помощи обратного преобразования получают решения дифференциального уравнения:
Пусть требуется найти решение линейных дифференциальных уравнений с постоянными коэффициентами.
где
где Преобразование Лапласа приводит к уравнению
где
Решением полученного уравнения имеет вид
Обратное преобразование только для второго слагаемого дает решение дифференциального уравнения с нулевыми начальными условиями. Пример 1.1. Тогда
Решение вспомогательного уравнения имеет вид
Для вычисления обратного преобразования раскладываем правую часть на простейшие дроби:
При помощи таблицы преобразования Лапласа по этому изображению находим оригинал:
Операторный метод удобно использовать также для решения линейных систем с постоянными коэффициентами. Пусть дана задача Коши:
при условии det(aik)¹0. Преобразование Лапласа
Из этой вспомогательной системы находим Yk (p), производим обратное преобразование и получим решение. Пример 1.2. Найти общее решение системы:
Пусть y1 (0)=с, y2(0)=с2. После преобразования получим
откуда
Выполнив обратное преобразование, получим общее решение
1.1.4.Преобразование дифференциальных уравнений Преобразование дифференциальных уравнений к нормальной форме Дифференциальное уравнение, разрешимое относительно старшей производной, всегда можно привести к нормальной системе. Рассмотрим линейное уравнение n - го порядка с постоянными коэффициентами:
или в символической форме
Такая система эквивалентна линейной системе n уравнений первого порядка, собственные значения которых равны корням полинома:
Пусть собственные значения системы - различные действительные числа. Предположим y(t) - решение уравнения (1.51) и определим n - мерную функцию x(t), примем
xi(t) - компоненты вектора x(t). Отсюда имеем:
В векторной форме эта система имеет вид:
или сокращенно:
С другой стороны, если x(t) – решение уравнения (1.57), то функция y=x1(t) – решение уравнения (1.51), т.е. полученная система n уравнений первого порядка эквивалентна одному уравнению n - го порядка. Чтобы убедиться в том, что собственные значения матрицы А системы (1.56) являются корнями полинома (1.53), найдем собственные значения матрицы А:
Детерминант матрицы (1.58) после раскрытия по минорам
или
где
Следовательно, уравнения (1.51) и (1.56) эквивалентны. Пример 1.3. Рассмотрим систему:
Полагая,
Матрица Собственные значения матрицы - корни полинома:
Допустим собственные значения матрицы А - действительные и различные числа l1,l2,....,ln и матрица собственных значений:
Существует невырожденная матрица Р, такая, что:
где Р - матрица Вандермонда
Детерминант матрицы Р равен
т.е. Р - невырожденная матрица, если все li различны. Представление в пространстве состояний при содержании только полюсов. В этом случае дифференциальное уравнение системы в символической форме имеет вид
где Передаточная функция
В общем случае корни характеристического уравнения комплексные
Начальные условия системы (всего
Из (1.66) следует, что
Из уравнения (1.64) следует
Следовательно
откуда вытекает, что
или
Вектор
где Следовательно,
Для выяснения физического смысла понятия состояния системы рассмотрим модель решения уравнения (1.70) (рис. 1.5).
Как видно по рис.1.5, переменные состояние X1(t),X2(t),…,Xn(t) соответствуют выходным сигналам интеграторов. Постоянные коэффициенты а0, а1,…, аn являются коэффициентами усиления в цепях каналов обратной связи. Так как собственные значения матрицы А
То они совпадают с полосами передаточной функции W(p) (1.65). Собственные значения являются инвариантным свойством линейного преобразования и матрица, связанная с линейным преобразованием, зависит от базисов векторных пространств, поэтому полюса передаточной функции (собственные значения матрицы) являются инвариантными величинами. При этом переменные состояния и матрицы могут быть различными. Случай, когда передаточная функция системы имеет полюса и нули Пусть объект с одним входом и одним выходом описывается линейным дифференциальным уравнением с постоянными коэффициентами
Передаточная функция
Здесь принято, что число нулей равно числу полюсов. В противном случае можно выбирать Обозначим через p1, p2, …, pn комплексные корни полинома знаменателя и s1, s2, …,sn - комплексные корни полинома числителя, т.е. p1, p2, …, pn – полюса, а s1, s2, …,sn – нули W(p). Тогда можно написать
Для того, чтобы решить дифференциальное уравнение (1.75), необходимо знать 2n начальных условий: y(o), y(o),…,y(n-1)(0) и U(0), U(0),…, U(n-1)(0). Найдем вектор состояния. Пусть X(t) – n – мерный вектор с компонентами x1(t), x2(t),…, xn(t), заданными соотношениями
где h0, h1,…, hn-1 - постоянные, которые необходимо найти. Соотношения (1.78) можно записать в виде
Найдем дифференциальное уравнение, которому удовлетворяет xi(t). Из (1.78) заключаем, что
Аналогично, можно получить
так как
Дифференцирование выражения (1.79) для i=n дает:
Дифференциальное уравнение (1.79) дает соотношение
Из выражения (1.82) следует, что
Следовательно
Путем непосредственных вычислений можно получить
Подставив это выражение в уравнение (1.86) и сгруппировав члены, получим
Выберем k таким образом, чтобы
Подставив выражение (1.89) в уравнение (1.88), получим дифференциальное уравнение
где
Полученные дифференциальные уравнения относительно xi(t) можно записать в векторной форме
или сокращенно
В развернутой форме вычисление hi, i=1,n имеет вид h0=b0, h1=bn-1-h0an-1, h2=bn-2-h0an-2-h1an-1 и т.д. (1.94) Вектор X(t) представляет вектор состояния системы (1.75), так как знание X(t0) и U(t0,t) полностью определяет решение дифференциального уравнения (1.93) на интервале [t0,t]. Поскольку выход y(t) равен Y(t)=x1(t)+h0U(t), (1.95) то y(t0,t) полностью определяется величинами X(t0) и U(t0,t). Случай, когда n>m Предположим, что в уравнении (1.75) bn=bn-1=…=bm+1=0; bm¹0, (1.96)
Выполним преобразования
где
можно рассматривать как вектор состояния системы с передаточной функцией (1.97). Дифференциальное уравнение имеет вид
Пример 1.4. Дана система
для которой n=3, a0=0, a1=2, a2=3, b3=0, b2=1, b1=7, b0=12. Из уравнения (1.91) находим h0=0, h1=1, h2=4, h3=-2. Фазовые координаты
Дифференциальное уравнение
Преобразование уравнений состояния При анализе и синтезе систем управления возникает необходимость преобразования линейных дифференциальных уравнений с постоянными коэффициентами. Пусть уравнение системы
Определим новую переменную состояния
где T-невырожденная nxn матрица. Подставляя (1.102) в (1.101), получим
откуда
Тогда
где Матрицы A и Q подобны, следовательно, имеют одинаковые собственные значения, поэтому вектор Z(t) можно рассматривать как вектор состояния системы.
Таким образом, по известному вектору Z(t) можно найти вектор X(t). Заменой переменных можно преобразовать модель системы управления. Это возможно, если собственными значениями матрицы системы (1.70) являются различные действительные числа. Как было показано выше (см 1.62), в этом случае можно отыскать невырожденную матрицу Р, которая является матрицей Вандермонда, такую, что
Если определить вектор состояния, положив
То Z(t) будет удовлетворять дифференциальному уравнению
Обозначим элементы P-1 через rij, i,j=1,2,…,n. Так как вектор B задан в виде B=[0 0 … 0 b0]T, то уравнение (1.107) можно записать:
где На рис. 1.6 приведена модель системы (1.107). Компоненты вектора состояния Zi(t) представляют собой выходные сигналы n интеграторов. Выход y(t)=x1(t) равен сумме Zi(t), т.е.
так как первая строка матрицы Вандермонда состоит целиком из единиц. Числа
где
Предположим, что в начале система находится в покое (начальные условия нулевые) и что приложен вход U(t), тогда
При этих же условиях из выражения (1.107) находим
Так как
Сравнивая (1.111) с (1.113), получим
т.е. элементы последнего столбца матрицы Преобразование подобия позволило заменить модель системы (рис.1.5) моделью (рис.1.6), коэффициенты усиления которой Устойчивость систем управления в пространстве состояний В общем случае система устойчива, если евклидова норма ||x(t)|| остается ограниченной при
для любого решения системы x(t). Если система неустойчива, то существует такое решение
Пусть собственные значения матрицы А будут
где Тогда критерий устойчивости гласит: система устойчива, если - - Система абсолютно устойчива, если Линеаризация уравнений систем В большинстве случаев системы описываются нелинейными дифференциальными уравнениями. В общем случае уравнение состояния имеет вид
Нелинейную систему можно линеаризировать. При этом принимают следующие допущения: - отклонения переменных достаточно ма
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 799; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.233.69 (0.01 с.) |

 (1.1)
(1.1) константы;
константы; :
: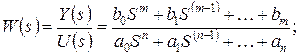 (1.2)
(1.2)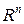 . Таким образом, за координаты вектора состояния принимаются выходные сигналы динамических объектов, обладающих свойством накапливать кинетическую или потенциальную энергию, вещество, положение и т.д. В качестве примера таких координат могут служить угол поворота вала электродвигателя, напряжение на конденсаторе и др. Многие элементы не являются идеальными интеграторами и должны рассматриваться с учетом их диссипативных свойств.
. Таким образом, за координаты вектора состояния принимаются выходные сигналы динамических объектов, обладающих свойством накапливать кинетическую или потенциальную энергию, вещество, положение и т.д. В качестве примера таких координат могут служить угол поворота вала электродвигателя, напряжение на конденсаторе и др. Многие элементы не являются идеальными интеграторами и должны рассматриваться с учетом их диссипативных свойств. (1.3)
(1.3)
 пространство управлений.
пространство управлений.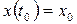 и определенном управлении
и определенном управлении  .
. (1.4)
(1.4) постоянные коэффициенты;
постоянные коэффициенты; возмущающие воздействия.
возмущающие воздействия. (1.5)
(1.5)
 называются векторами. Вектор X называют фазовым вектором или вектором состояния, а его координаты x1,..., xn - фазовыми координатами. Вектор U называют вектором управления или просто управлением, а его координаты u1 ,..., um - параметрами управления.
называются векторами. Вектор X называют фазовым вектором или вектором состояния, а его координаты x1,..., xn - фазовыми координатами. Вектор U называют вектором управления или просто управлением, а его координаты u1 ,..., um - параметрами управления. (1.6)
(1.6) (1.7)
(1.7)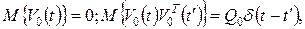 (1.8)
(1.8)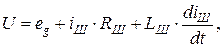 (1.9)
(1.9) (1.10)
(1.10) (1.11)
(1.11) - момент на валу,
- момент на валу, (1.12)
(1.12) (1.13)
(1.13) , (1.14)
, (1.14) . (1.15)
. (1.15) (1.16)
(1.16)
 . (1.17)
. (1.17)
 (1.18)
(1.18) .
.
 (1.19)
(1.19) - обобщенные координаты,
- обобщенные координаты, и
и  .
.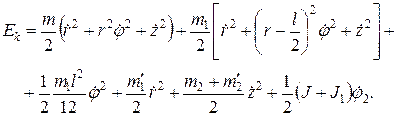 (1.20)
(1.20) (1.21)
(1.21) - ускорение свободного падения.
- ускорение свободного падения.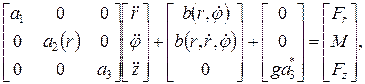 (1.22)
(1.22)
 вектор ускорений,
вектор ускорений, вектор, обусловленный силами инерции от взаимного влияния движений по координатам r и j,
вектор, обусловленный силами инерции от взаимного влияния движений по координатам r и j, 
 - компоненты вектора, обусловленные соответственно центробежной и кориолисовой силами инерции,
- компоненты вектора, обусловленные соответственно центробежной и кориолисовой силами инерции, вектор сил тяжести,
вектор сил тяжести,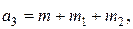
 вектор обобщенных сил,
вектор обобщенных сил,
 .
.

 . (1.23)
. (1.23)



 , (1.24)
, (1.24) (1.25)
(1.25)

 (1.26)
(1.26) (1.27)
(1.27) . (1.28)
. (1.28) (1.29)
(1.29)
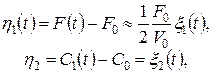


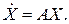 (1.30)
(1.30)
 образует n линейно - независимых решений этого уравнения.
образует n линейно - независимых решений этого уравнения. (1.31)
(1.31)
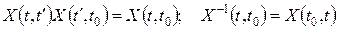 .
. (1.32)
(1.32) . (1.33)
. (1.33) . (1.34)
. (1.34) (1.35)
(1.35) (1.36)
(1.36)
 (1.37)
(1.37) (1.38)
(1.38) (1.39)
(1.39)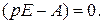 (1.40)
(1.40) (1.41)
(1.41) . (1.42)
. (1.42) называется экспоненциальной матрицей или матричным экспоненциалом и определяется суммой ряда:
называется экспоненциальной матрицей или матричным экспоненциалом и определяется суммой ряда: (1.43)
(1.43) (1.44)
(1.44) то формулу Коши представляют в виде
то формулу Коши представляют в виде (1.45)
(1.45) .
. (1.46)
(1.46) .
. , (1.47)
, (1.47) постоянные.
постоянные. (1.48)
(1.48)
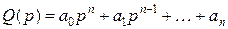 , или сокращено
, или сокращено . (1.49)
. (1.49) (1.50)
(1.50)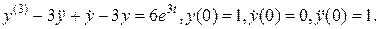
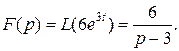



 .
. ,
, .
. приводит к системе
приводит к системе .
. .
.

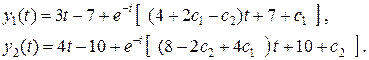
 , (1.51)
, (1.51)
 (1.52)
(1.52) . (1.53)
. (1.53)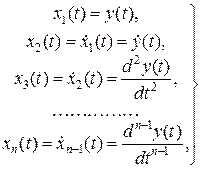 (1.54)
(1.54) (1.55)
(1.55) . (1.56)
. (1.56)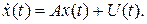 (1.57)
(1.57) . (1.58)
. (1.58) (1.59)
(1.59)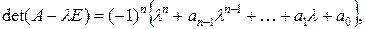 (1.60)
(1.60) является собственным значением матрицы А в том и только в том случае, когда l - корень полинома (1.53), т.е.
является собственным значением матрицы А в том и только в том случае, когда l - корень полинома (1.53), т.е.
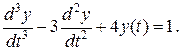
 получим систему:
получим систему:
 .
.
 . (1.61)
. (1.61) (1.62)
(1.62)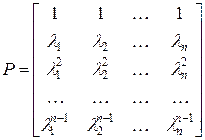 . (1.63)
. (1.63)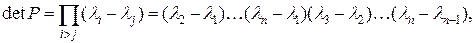
 (1.64)
(1.64) - скалярный выход,
- скалярный выход,  - скалярный вход.
- скалярный вход. (1.65)
(1.65) будут полюсами
будут полюсами  , поэтому
, поэтому
 ) -
) -  . По аналогии с (1.54) определяем
. По аналогии с (1.54) определяем 
 (1.66)
(1.66) (1.67)
(1.67) (1.68)
(1.68) (1.69)
(1.69) удовлетворяет системе дифференциальных уравнений, которые в матричной форме имеют вид
удовлетворяет системе дифференциальных уравнений, которые в матричной форме имеют вид , (1.70)
, (1.70) (1.71)
(1.71)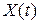 представляет собой переменную состояния системы (1.64), поскольку знание
представляет собой переменную состояния системы (1.64), поскольку знание  и выход
и выход  . Если
. Если  и
и  известны, то единственное решение уравнения (1.71) с
известны, то единственное решение уравнения (1.71) с  (1.72)
(1.72) - фундаментальная матрица уравнения (1.66).
- фундаментальная матрица уравнения (1.66).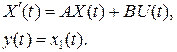 (1.73)
(1.73)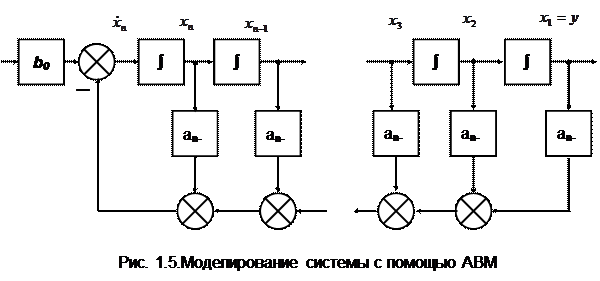
 являются корнями полинома
являются корнями полинома . (1.74)
. (1.74) (1.75)
(1.75)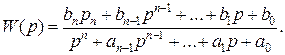 (1.76)
(1.76) тогда будем иметь m нулей и n полюсов.
тогда будем иметь m нулей и n полюсов. (1.77)
(1.77) (1.78)
(1.78) (1.79)
(1.79) (1.80)
(1.80)
 (1.81)
(1.81)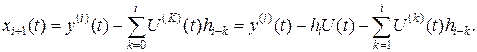 (1.82)
(1.82) (1.83)
(1.83) (1.84)
(1.84) (1.85)
(1.85) (1.86)
(1.86) (1.87)
(1.87)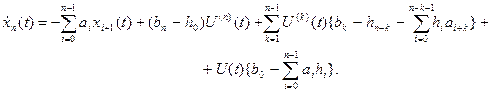 (1.88)
(1.88) не зависела от всех производных U(t). Это можно сделать, положив n0=b0,
не зависела от всех производных U(t). Это можно сделать, положив n0=b0, для
для  (1.89)
(1.89) (1.90)
(1.90) (1.91)
(1.91) , (1.92)
, (1.92) (1.93)
(1.93) (1.97)
(1.97) (1.98)
(1.98) , (1.99)
, (1.99) . (1.100)
. (1.100)
 определяются соотношением (1.90):
определяются соотношением (1.90):
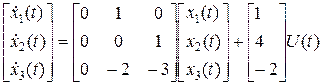 .
. (1.101)
(1.101) , (1.102)
, (1.102)
 (1.103)
(1.103) (1.104)
(1.104)
 . (1.105)
. (1.105) . (1.106)
. (1.106) .
. (1.107)
(1.107)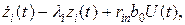 (1.108)
(1.108) -собственные значения матрицы системы, rin-элементы последнего (n-го) столбца матрицы P-1.
-собственные значения матрицы системы, rin-элементы последнего (n-го) столбца матрицы P-1. (1.109)
(1.109)
 в (1.108) можно вычислить непосредственно, проинвертировав матрицу P. Более рациональным способом можно получить эти числа следующим способом. Так как полюса W(p) расположены при p=li, можно написать
в (1.108) можно вычислить непосредственно, проинвертировав матрицу P. Более рациональным способом можно получить эти числа следующим способом. Так как полюса W(p) расположены при p=li, можно написать (1.110)
(1.110) представляет собой вычет W(p) в i-м полюсе li. Так как =li различны, имеем
представляет собой вычет W(p) в i-м полюсе li. Так как =li различны, имеем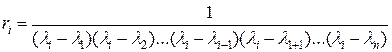 .
.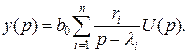 (1.111)
(1.111) (1.112)
(1.112) , то
, то (1.113)
(1.113)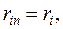 (1.114)
(1.114)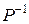 равны вычетам W(p).
равны вычетам W(p). равны вычетам передаточной функции W(p) в полюсах
равны вычетам передаточной функции W(p) в полюсах  соответственно.
соответственно. для любого решения x(t) системы. Систему называют абсолютно устойчивой в том и только в том случае, если
для любого решения x(t) системы. Систему называют абсолютно устойчивой в том и только в том случае, если , (1.115)
, (1.115) , при котором
, при котором (1.116)
(1.116)
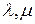 - действительные числа,
- действительные числа, 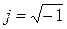 .
. для всех i в случае, когда корни – действительные числа;
для всех i в случае, когда корни – действительные числа; для всех k в случае кратных корней вида
для всех k в случае кратных корней вида  .
.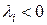 для любого i.
для любого i. . (1.117)
. (1.117)


