
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наблюдаемость и восстанавливаемостьСодержание книги
Поиск на нашем сайте
При синтезе оптимальных систем управления с обратной связью получают управляющие воздействиякак функции фазовых координат. Обычно измерению поддаются лишь векторы выходных координат объекта, а другие фазовые координаты являются лишь абстрактными понятиями. В связи с этим возникают проблемы наблюдаемости и восстанавливаемости, заключающиеся в установлении возможности определения состояния объекта (фазового вектора) по измеренным значениям выходной переменной на некотором интервале. Пусть объект описывается уравнением
а выходящая переменная связана с фазовыми координатами соотношением
которое называется уравнением наблюдения. Система (1.146) и (1.147) называется вполне или полностью наблюдаемой, если существует такое t1, t<t1<∞, что по данным измерения Полная наблюдаемость означает, что имеется возможность определить состояние х(t) по будущим значениям выходной переменной. Однако в задачах управления текущее состояние объекта должно определяться по прошлым значениям выходной переменной, поэтому более важным является полная восстанавливаемость. Система (1.146) и (1.147) называется вполне или полностью восстанавливаемой, если существует такое t0, ∞<t0< t, что по данным измерения y( Для стационарных систем из полной наблюдаемости следует полная восстанавливаемость и наоборот. Рассмотрим непрерывную линейную систему
для Пусть требуется определить х(t), измеряя у(t) на некотором интервале Этот вопрос также легко решается, если С(t) имеет размер nхn и несингулярна только для одного значения t=t*≥t0. Действительно, заметим, что х(t)=С-1(t*)у(t*). Так как общее решение уравнения (1.146) имеет вид
но при t=t*
откуда следует, что
где Подставляя х(t0) из (1.151) в (1.150), получаем х(t) для всех t≥t0, так как U(τ) известно для всех t≤t0. Однако, если матрица С(t) размера nxn сингулярна для всех t≥t0 или, если размер матрицы С(t) mхn, m<n, то необходимо специально исследовать вопрос о возможности определения х(t), по измеренным Необходимое и достаточное условие полной наблюдаемости системы дает следующая теорема. Непрерывная линейная система (1.148) и (1.149) является полностью наблюдаемой тогда и только тогда, когда симметричная матрица размера nxn
положительно определена для некоторого конечного t1>t0. Доказательство. Так как предполагается, что U(t) известна для всех t≥t0, то легко определить воздействие управления на состояние х(t): 
т.е. достаточно рассмотреть систему вида
где t≥t0. Достаточность. Подставляя решение (1.153) в виде х(t)=К(t,t0)х(t0) в уравнение (1.154), получаем
Умножая это уравнение слева на
или если обозначить
то из (1.155) следует, что
и система, очевидно, будет полностью наблюдаемой, если М(t0,t1) не вырождена для t>t0. Необходимость. Предположим, что система наблюдаема, но М(t0,t1) не является положительно определенной, т.е. для некоторого х(t0)≠0
(Случай В силу (1.155) это означает, что
Учитывая, что
откуда у(t)=0 для t0≤t≤t1. Следовательно, существует отличное от нуля состояние х(t0), которое нельзя определить, зная 1.3.1.Наблюдаемость линейных систем Рассмотрим линейную стационарную систему
Введем матрицу наблюдаемости
Ее размерность (nхnρ). Для системы(1.158), (1.159) справедлив следующий критерий полной наблюдаемости: система (1.158), (1.159) вполне наблюдаема (восстанавливаема) тогда и только тогда, когда ранг матрицы наблюдаемости равен n. Транспонированная матрица
имеет такой же ранг, что и матрица (1.160), поэтому вместо исходной матрицы наблюдаемости можно рассматривать транспонированную. Доказательство. Необходимость. Пусть rank HT<n. Тогда размерность пространства RH является собственным подпространством пространства Rn. Поэтому существует ненулевой вектор x^ÎRn, ортогональной всем строкам матрицы HT (таким вектором является любой вектор из Rn,не принадлежащий подпространству RH):
На основании теоремы Гамильтона-Кэли
откуда по индукции следует, что матрица Ак при к ³ n линейно выражается через Е, А, …, Аn-1, поэтому из (1.162) получаем, что Следовательно:
Пусть некоторому начальному условию х(0) = х(l) соответствует выходная переменная y(l)(t). В силу соотношения (1.163) всем начальным условиям вида x(0)=x(l)+x соответствует та же выходная переменная y(l)(t):
Таким образом, определить состояние х(0) по значениям выходной переменной, если rank HT<n, невозможно, что и доказывает утверждение. Достаточность. Пусть rank НТ=n. В силу стационарности системы достаточно показать возможность определения состояния х(0) по известным значениям выходной переменной и управления на некотором интервале [0.t]. Имеем:
или
Так как y(t) и U(t) измеряются, матрицы С и А заданы, то функция Dy(t) и ее производные любого порядка являются известными функциями времени. Из последнего соотношения при t=0 получаем:
или
Полученное векторное уравнение с n неизвестными xi(0) Наблюдаемость (восстанавливаемость) системы (1.158) полностью определяется матрицами А и С. Свойство наблюдаемости (восстанавливаемости) не зависит от выбора системы координат. 1.3.2.Каноническая форма наблюдаемости Пусть ранг матрицы Н равен m (m<n). Это означает, что подпространство невосстанавливаемых состояний имеет размерность (n-m). Вектор - строки Н порождают m-мерное линейное подпространство с базисом t1, t2,…, tm. За базис этого подпространства (подпространства восстанавливаемости) можно принять m независимых вектор - строк матрицы Н, или вектор - строки ti, i = Пусть tm+1, tm+2,…,tn -(n-m) линейно независимых вектор- строк, которые вместе с t1, t2,…,tm порождают все n-мерное пространство. Составим необходимую матрицу преобразования:
где Преобразованные уравнения состояния и наблюдения принимают вид:
Пусть Т-1=[P1P2], где Р1 – подматрица из m столбцов, Р2 – подматрица из (m-n) столбцов. Из ТТ-1=Е (уравнение 1.19) следует, что Т1Р2=Т2Р1=0. Это означает, что любой вектор х, удовлетворяющий условию Т1х=0, удовлетворяет условию Нх=0 и принадлежит подпространству невосстанавливаемых состояний. Используя замены для уравнений состояния и наблюдения, можно записать
В этом выражении строки матрицы А, Aj, j=
а для строк, содержащих также координаты в общем случае Так как все столбцы Т1 являются базисом в подпространстве восстанавливаемости, можно показать, что Т2АР1¹0 в общем случае. Поскольку строки матрицы С являются строками матрицы Н (т.е. принадлежат подпространству восстанавливаемости), а столбцы Р2 принадлежат подпространству невосстанавливаемости состояний, то СР2=0. Таким образом, уравнение состояния и наблюдения принимает вид:
где Никакие суждения о Другая форма записи:
Схематически рассмотренный случай можно проиллюстрировать структурной схемой (рис. 1.9), где представлена вполне управляемая система S, так как управление воздействует на все составляющие фазового вектора. Однако система не является наблюдаемой, так как координаты хк+1,…,хn не влияет на результаты измерения величины y(t).
Матрица наблюдаемости и ранг равны:
Следовательно, система не вполне наблюдаема. Невосстанавливаемой координатой является х1. Тогда в качестве базиса RH можно принять строки:
которые дополним строкой Матрицы Т и Т-1 имеют вид:
Тогда получим:
и уравнение состояния и наблюдения принимает вид:
или
1.3.3.Обнаруживаемость Если система не вполне наблюдаема, то любой фазовый вектор можно представить в виде суммы
где хн(t) – вектор из подпространства наблюдаемости, х^(t) – полностью невосстанавливаемый нулевой вектор. Вектор х(t) восстанавливается по наблюдениям y(t) и U(t) на интервале t0£t£t c точностью до невосстанавливаемого вектора х^. Вектор х(t) становится асимптотически восстанавливаемым, если х^(t)®0 при t®¥. Поэтому важным является следующее понятие Системы (1.158), (1.159) называются обнаруживаемыми, если невосстанавливаемые координаты при нулевых остальных координатах и нулевом входном воздействии стремится к нулю при t®¥. Следовательно, вполне наблюдаемая система является обнаруживаемой. Также является обнаруживаемой любая асимптотически устойчивая система. Из канонической формы наблюдаемости следует, что система является обнаруживаемой в том и только в том случае, если матрица А22 является асимптотически устойчивой, т.е. все собственные значения ее имеют отрицательные вещественные части. 1.3.4.Принцип двойственности управляемости и наблюдаемости Рассмотрим наряду с системой
так называемую двойственную ей систему
Здесь принято Д=0, поскольку эта матрица не влияет на управляемость и наблюдаемость системы. Из условия критериев управляемости и наблюдаемости систем можно получить следующий принцип двойственности: система (1.168) вполне наблюдаема тогда и только тогда, когда двойственная ей система (1.169) вполне управляема, и система (1.168) вполне управляема тогда и только тогда, когда двойственная ей система вполне наблюдаема. Пример 1.7. Рассмотрим наблюдаемость и обнаруживаемость системы.
здесь
Матрица наблюдаемости:
При С¹0 rank HT=2, следовательно, система вполне наблюдаема. При С=0 rank HT=1 и система не вполне наблюдаема. Наблюдаемой является координата х1. Матрица, определяющая обнаруживаемость системы, равна нулю, и ее собственные значения также равны нулю. Следовательно, при с=0 система является также и обнаруживаемой. 1.3.5.Наблюдатели Перейдем от вопроса возможности восстановления к вопросу синтеза устройства, восстанавливающего текущее значение фазового вектора. Восстановленное значение фазового вектора называется его оценкой, а устройство, обеспечивающее получение оценки по измерениям управления U(t) и выходной переменной y(t) на интервале t0£t£t, - наблюдателем (фильтром). Наблюдатели полного порядка Пусть имеется линейная наблюдаемая система, описываемая соотношениями:
Если С(t) не вырождена, то вектор состояния х(t) может быть легко найден из выражения
Измеритель попытаемся подобрать так, чтобы
где Т – невырожденная матрица. Если (1.170) умножить на Т, а (1.173) продифференцировать по t, то получим (опуская везде аргумент t)
и, используя (1.173), подставим в (1.172)
Полагаем, что (1.174) должно выполняться при всех реализациях x(t) и U(t). Тогда (1.174) справедливо, если только
Если матрицы F и A не имеют общих собственных значений, то можно показать, что при фиксированных матрицах F,A и С уравнение (1.175) будет иметь единственное решение относительно Т. Таким образом, чтобы построить измеритель, нужно конкретизировать F или Т, с помощью которых уже можно найти G. Матрицы А, В, С и Н являются неизменяемыми. Если (1.170) умножить на Т и вычесть полученное выражение из (1.172), то получим
которое после учета (1.212) и (1.213) приобретает вид
Последнее уравнение имеет решение
где
Е – единичная матрица. Из (1.180) следует, что искомый результат q(t)=Tx(t) - начальное условие в виде
Следует учесть, что в реальности можно установить правильно начальные условия. Тогда требуется, чтобы Отметим, что для систем с переменными параметрами отрицательность действительных частей собственных значений матрицы F(t) еще не обеспечивает устойчивости системы. Из (1.173) следует, что Т является матрицей размером nxn, и тогда x(t) может быть получен из (1.173) после инвертирования Т. Так как процесс инвертирования Т не всегда прост, желательно исключить эту процедуру выбором Т в виде единичной матрицы Е. Тогда из (1.175) и (1.176) следует
И, подставив все в (1.172), получим уравнение измерителя
В последнем уравнении матрицу Н можем представить в виде Н=КС, где К – неизвестная (искомая) матрица. Учитывая (1.171), получим
структура измерителя, описываемого уравнением (1.184), может быть представлена схемой (рис.1.10). Из уравнения (1.177) при учете (1.175) и (1.176) Т=Е и Н=КС получим, что
или, подразумевая под е(x-q) ошибку измерения, получим
Отсюда следует зависимость устойчивости наблюдателя от матрицы А-КС, а именно, что От матрицы А-КС зависит еще и качество наблюдателя, т.е. насколько быстро ошибка стремится к нулю. Следовательно, синтез наблюдателя сводится к выбору матрицы К из условия устойчивости и заданных требований к качеству. Если матрица системы и матрица коэффициентов усиления постоянны (стационарный наблюдатель), устойчивость и качество наблюдателя зависят от расположения корней его характеристического уравнения, т.е. собственных значений матрицы А–КС на комплексной плоскости. Если исходная система (пара А, С) вполне наблюдаема, собственные значения матрицы А-КС могут быть произвольно размещены на комплексной плоскости. Если система не вполне наблюдаема, то можно найти такую постоянную матрицу К, при которой наблюдатель асимптотически устойчив в том и только в том случае, если система обнаруживаема. Пример 1.8. Построим наблюдатель полного порядка для системы
Для рассмотренной системы можно записать
В уравнении (1.184) неизвестную матрицу К представим в виде
Тогда получим
где функции К1(t) и К2(t) можно выбрать таким образом, чтобы собственные значения матрицы
Для обеспечения устойчивости измерителя следует выбрать К1,К2> 0, а для большей простоты можем положить Таким образом, выходной сигнал такого измерителя определяется соотношением
где
В последнем примере уравнение наблюдения имело вид y=x1(t), и был определен измеритель для восстановления вектора состояния x(t). Причем порядок (т.е. размерность) измерителя совпадал с порядком вектора состояния. Некоторая часть данных измерителя является избыточной (излишней). Действительно, переменная x1(t) вектора состояния получена как компонента выходного сигнала измерителя, хотя x1(t) уже можно наблюдать как выходной сигнал рассматриваемой системы [y=x1(t)]
Очевидно, что все математические преобразования раздела 4.1 остаются справедливыми, только в уравнении q(t)=Tx(t) матрица Т имеет размер - собственные значения матрицы измерителя разные и отличаются от собственных значений матрицы исходной системы; - исходная система и измеритель полностью наблюдаемы; - измеритель имеет порядок не менее (n-m); - структура измерителя и системы должны быть неизменны во времени. Итак, рассмотрим систему и наблюдатель
y(t)=Cx(t), (1.186) где А, B, C – постоянные матрицы, x(t) – n – вектор, y(t) – m – вектор (m< n). Положим, что ранг матрицы С максимален, т.е. rank C = m. Линейную оценку общего типа вектора состояния системы опишем уравнением.
Ошибку оцениваем e=x(t)- и ее производную оценим по следующей схеме
Из требования несмещенности оценки
тогда, вычисляя математические ожидания левой и правой частей (1.188), получаем F(t)=A(t)-GC(t), (1.189) откуда следует после подстановки (1.184) в (1.182)
Последнее уравнение описывает измеритель с произвольной структурой, формирующей несмещенные оценки вектора состояния. Однако структура этого измерителя избыточна, так как формирует оценки для полного вектора состояний, хотя часть из них доступна прямым измерениям из уравнения y=Cx. Поэтому можно строить измеритель пониженного порядка. Люенбергером доказана теорема о том, что для любой вполне управляемой линейной системы n-го порядка с инвариантной во времени структурой, имеющей m линейно независимых выходов, можно построить измеритель состояния порядка n-m с произвольными собственными значениями. Для этого систему (1.170) разобьем на две подсистемы
где значение вектора
Эта система является аналогом для системы (а) и (b), для которой измеритель определяется соотношением (1.185). Учитывая замены обозначений:
получим уравнение для измерителя пониженного порядка. Произведение
Для компенсации участия производной, положим
и тогда
с условием Пример 1.9. Рассмотрим систему
и процесс наблюдения Требуется построить измеритель пониженного порядка, т.е. измеритель, формирующий значения Исходя из условий задачи, имеем:
На основании (1.197) и (1.198) можно записать:
Если принять произвольно G=2, получим:
Можно заметить, что
Таким образом, eà0 при tà¥. Несколько иной подход можно использовать следующим образом. Введем такой (n-m)-вектор p(t), осуществляющий соотношение
что матрица Из уравнения Используя представление
где L1 и L2 – (n-m) и [n x (n-m)] – матрицы соответственно, получим
Если получит оценку p(t) для введенного вектора, то для оценки фазового вектора имеем:
Таким образом, задача восстановления фазового вектора свелась к задаче восстановления вектора p(t) меньшей размерности. Для построения наблюдателя для переменной p(t) найдем для этой переменной дифференциальное уравнение. Дифференцируя (1.199) и используя (1.185), (1.186), получим:
или с учетом (1.200)
Чтобы воспользоваться структурой наблюдателя (1.184), необходимо (1.203) дополнить исходным уравнением наблюдения y=Cx=CL1y+C|L2p, так как CL2 =0, и переменная y не зависит от p. Действительно, из (1.199) имеем:
откуда CL2 =0. Примем в качестве уравнения наблюдения уравнение, которое получается дифференцированием выражения y=Cx: Тогда наблюдатель для p описывается уравнением:
В это уравнение входит производная
И искомая оценка
Уравнения (1.205) и (1.206) определяют искомый наблюдатель. Пример 1.10. Для системы
построить наблюдатель полного и пониженного порядков. Здесь
Наблюдатель полного порядка (см. формулу (1.221)):
В скалярной форме
Для построения наблюдателя пониженного порядка используем формулы (1.204), (1.205) и определим матрицы Матрица
Откуда
Подставляя выражение для
где K выбирается из условия устойчивости и заданных требований к качеству управления.
|
||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 829; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.192.174 (0.014 с.) |


 (1.146)
(1.146) , (1.147)
, (1.147) на интервале
на интервале  можно определить состояние х(t).
можно определить состояние х(t). ) на интервале
) на интервале  можно определить значение х(t).
можно определить значение х(t). (1.148)
(1.148) , (1.149)
, (1.149) . Положим, что u(t) является известной функцией времени для всех
. Положим, что u(t) является известной функцией времени для всех  . Очевидно, если С(t) имеет размер nхn и несингулярно для всех
. Очевидно, если С(t) имеет размер nхn и несингулярно для всех  , то х(t)=С-1(t)у(t) и вопрос о наблюдаемости решается тревиально.
, то х(t)=С-1(t)у(t) и вопрос о наблюдаемости решается тревиально. (1.150)
(1.150)

 (1.151)
(1.151) .
. при некотором конечном t1.
при некотором конечном t1.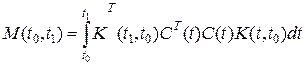 , (1.152)
, (1.152) , (1.153)
, (1.153) , (1.154)
, (1.154)
 и интегрируя от t0 до t1, получаем:
и интегрируя от t0 до t1, получаем: , (1.155)
, (1.155)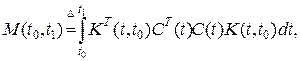 (1.156)
(1.156) , (1.157)
, (1.157)
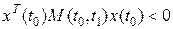 исключает в силу определения матрицы М).
исключает в силу определения матрицы М). .
. после подстановки в это выражение уравнения (1.154) получим (х(t0) ≠0)
после подстановки в это выражение уравнения (1.154) получим (х(t0) ≠0)
 , что противоречит предположению о наблюдаемости системы. В общем случае условие М(t0,t1)>0 трудно использовать из-за большого объема вычислений, однако для стационарных систем применимо более удобное следствие рассматриваемой теоремы.
, что противоречит предположению о наблюдаемости системы. В общем случае условие М(t0,t1)>0 трудно использовать из-за большого объема вычислений, однако для стационарных систем применимо более удобное следствие рассматриваемой теоремы. (1.158)
(1.158) (1.159)
(1.159) . (1.160)
. (1.160) , (1.161)
, (1.161) . (1.162)
. (1.162)
 при всех l=0,1,2,…
при всех l=0,1,2,… . (1.163)
. (1.163)
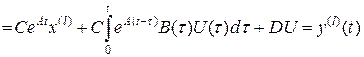 .
. ,
, .
.
 .
. равносильно системе из n´r уравнений. Так как по условию rank HT<n, то среди nr уравнений имеется ровно n независимых уравнений. На этом доказательство заканчивается.
равносильно системе из n´r уравнений. Так как по условию rank HT<n, то среди nr уравнений имеется ровно n независимых уравнений. На этом доказательство заканчивается. с отличными от нуля элементами только на местах рассматриваемых наблюдаемых координат.
с отличными от нуля элементами только на местах рассматриваемых наблюдаемых координат.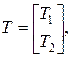
 .
.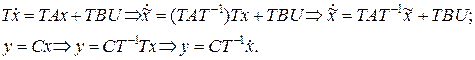
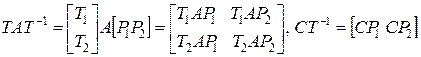 . (1.164)
. (1.164)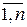 , не содержащие невосстанавливаемых координат, удовлетворяют условию
, не содержащие невосстанавливаемых координат, удовлетворяют условию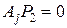 , (1.165)
, (1.165) , т.е. столбцы АР2 состоят из векторов, принадлежащих пространству невосстанавливаемых координат, а, следовательно, Т1АР2=0,
, т.е. столбцы АР2 состоят из векторов, принадлежащих пространству невосстанавливаемых координат, а, следовательно, Т1АР2=0,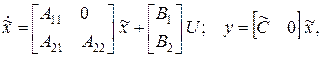
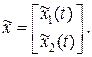
 по наблюдению y(t) не может быть, так как y(t) не зависит от х2(t).
по наблюдению y(t) не может быть, так как y(t) не зависит от х2(t).
 . (1.166)
. (1.166)
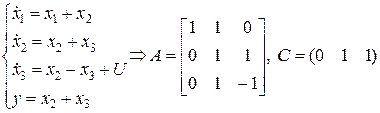 .
.
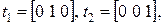
 .
. .
.


 , (1.167)
, (1.167) , (1.168)
, (1.168) . (1.169)
. (1.169)


 (1.170)
(1.170) . В противном случае вектор y(t) можно интерпретировать как входное воздействие для линейной наблюдаемой системы (измерителя), описываемой уравнением:
. В противном случае вектор y(t) можно интерпретировать как входное воздействие для линейной наблюдаемой системы (измерителя), описываемой уравнением: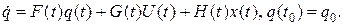 (1.172)
(1.172) , (1.173)
, (1.173)
 . (1.174)
. (1.174) (1.175)
(1.175) . (1.176)
. (1.176) , (1.177)
, (1.177) . (1.178)
. (1.178) (1.179)
(1.179) (1.180)
(1.180) . (1.181)
. (1.181) являлось матрицей перехода устойчивой системы или чтобы все собственные значения матрицы F(t) имели отрицательные вещественные части, что обеспечит быстрое угасание переходного процесса, обусловленного ошибкой установки начальных значений, и измеритель будет «хорошим».
являлось матрицей перехода устойчивой системы или чтобы все собственные значения матрицы F(t) имели отрицательные вещественные части, что обеспечит быстрое угасание переходного процесса, обусловленного ошибкой установки начальных значений, и измеритель будет «хорошим». ,
,  . (1.182)
. (1.182) . (1.183)
. (1.183) , (1.184)
, (1.184)


 при
при  независимо от начальной ошибки
независимо от начальной ошибки  тогда и только тогда, когда наблюдатель является асимптотически устойчивым. Из этих условий необходимо определять матрицу коэффициентов усиления К.
тогда и только тогда, когда наблюдатель является асимптотически устойчивым. Из этих условий необходимо определять матрицу коэффициентов усиления К. .
. .
. .
.
 были неположительными, что обеспечит «хороший» переходный процесс. Лучше всего положить k1 и k2 постоянными. Тогда:
были неположительными, что обеспечит «хороший» переходный процесс. Лучше всего положить k1 и k2 постоянными. Тогда: ,
, ,
, .
. . В этом случае
. В этом случае  .
. ,
, .
.

 и не может быть обращена. Присоединим к вектору q(t) компоненту, каждая из которых является линейно независимой комбинацией компонент вектора Х(t). Тогда придем к представлению
и не может быть обращена. Присоединим к вектору q(t) компоненту, каждая из которых является линейно независимой комбинацией компонент вектора Х(t). Тогда придем к представлению  , в котором матрица
, в котором матрица  имеет размер
имеет размер 
 и для нее будет существовать обратная матрица, если:
и для нее будет существовать обратная матрица, если: , (1.185)
, (1.185) . (1.187)
. (1.187) ,
, (1.188)
(1.188)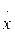 для каждого момента времени следует, что
для каждого момента времени следует, что

 . (1.190)
. (1.190) , (1.191)
, (1.191) , (1.192)
, (1.192) доступны точному измерению, а значения
доступны точному измерению, а значения  должны быть оценены. Очевидно, что если
должны быть оценены. Очевидно, что если  и u, а
и u, а  . (1.194)
. (1.194) ,
,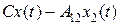 ,
, ,
,
 , (1.195)
, (1.195) используем с заменой из (1.194), получая
используем с заменой из (1.194), получая (1.196)
(1.196) , (1.197)
, (1.197) (1.198)
(1.198) .
. .
. .
. по измерениям
по измерениям 
 .
. ,
, .
.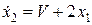
 .
.
 .
. . (1.199)
. (1.199) является не особой.
является не особой.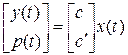 следует
следует  .
. . (1.200)
. (1.200) . (1.201)
. (1.201) . (1.202)
. (1.202) ,
, . (1.203)
. (1.203) ,
, .
. . (1.204)
. (1.204) . Чтобы избавиться от нее, введем дополнительную переменную
. Чтобы избавиться от нее, введем дополнительную переменную  . Тогда
. Тогда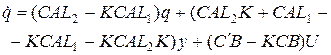 . (1.205)
. (1.205) . (1.206)
. (1.206) .
. .
. .
. .
. .
. должна быть такой, чтобы матрица
должна быть такой, чтобы матрица  была не особой. В остальном она может быть произвольной. Такому условию удовлетворяет матрица
была не особой. В остальном она может быть произвольной. Такому условию удовлетворяет матрица  . Из (1.235) находим
. Из (1.235) находим .
. .
. в (1.205) и (1.206), получим
в (1.205) и (1.206), получим ,
,


