
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Адаптивные автоматические системы управленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
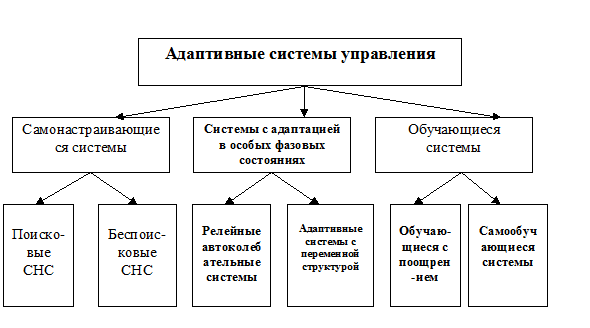
Адаптация – свойство приспособления к изменениям окружающей среды. Неадаптивные методы управления предусматривают наличие достаточного объема информации о внутренних и внешних условиях работы еще на предварительных стадиях синтеза. Создание адаптивных систем управления осуществляется в случае их функционирования в условиях неопределенности. Приспособление к изменяющимся условиям в адаптивных системах достигается за счет того, что часть функций по получению, отработке и анализу недостающей информации об управляемом процессе осуществляется самой системой в процессе ее нормальной эксплуатации. К адаптивному управлению приходится обращаться тогда, когда сложность управляемого процесса достигает такого уровня, при котором влияние неопределенности или неполной априорной информации об условиях работы системы становится существенным для обеспечения заданного качества процессов управления. Классификация адаптивных систем. В зависимости от способов реализации контролируемых изменений в процессе нормальной эксплуатации системы можно провести следующую классификацию адаптивных систем: - самонастраивающиеся системы; - системы с адаптацией в особых фазовых состояниях; - обучающиеся системы. Самонастраивающиеся системы Самонастраивающиеся системы (СНС) характеризуются наличием специальных контуров самонастройки, с помощью которых оцениваются динамические и статические свойства системы и формируются такие контролируемые воздействия, что система самопроизвольно приближается к определенному эталону, зачастую задаваемому математически в виде критерия качества функционирования. При этом контур самонастройки служит для изменения параметров или структуры основного контура с целью обеспечения заданного критерия качества управления. В процессе работы системы значение функционала качества изменяется, и задача контура самонастройки сводится к обеспечению экстремального значения критерия. Нахождение и поддержание экстремального значения критерия качества управления может производиться или с помощью пробных отклонений, или путем аналитического определения условий экстремума. В зависимости от способа нахождения экстремума выделяют поисковые и беспоисковые СНС.
Поисковые системы в зависимости от применяемых методов могут быть: - со случайным поиском; - с поиском по методу Гаусса - Зайделя (пошагового спуска); - с поиском по методу градиента; - с поиском по методу найскорейшего спуска. В классе беспоисковых СНС выделяют системы: - с использованием информации о частотных характеристиках; - с контролем временных характеристик; - с эталонными моделями; - градиентные СНС.
Рис. 2.1. Класссификация адаптивных систем управления
Системы с адаптацией в особых фазовых состояниях Системы с адаптацией в особых фазовых состояниях используют особые режимы или свойства нелинейных систем, например, режим автоколебаний, скользящие режимы для организации контролируемых изменений динамических свойств системы управления. Специально организованные особые режимы в таких системах либо служат дополнительным источником рабочей информации об изменяющихся условиях функционирования системы, либо наделяют систему управления новыми свойствами, за счет которых динамические характеристики управляемого процесса поддерживаются в желаемых пределах независимо от возникших при функционировании изменений. Эти системы можно подразделить на релейные автоколебательные и адаптивные системы с переменной структурой. Обучающиеся системы Обучающиеся системы управления характеризуются наличием специальных процессов обучения, которые заключаются в постепенном накапливании, запоминании и анализе информации о поведении системы и изменении законов функционирования в зависимости от приобретаемого опыта. Накопление и обобщение информации в процессе обучения можно осуществлять за счет внесения “эталонного опыта” в систему извне либо путем формирования такого опыта внутри системы. Поведение системы в ответ на такую обучающую последовательность ситуаций формируют на основе принципа «поощрение – наказание», т.е. правильная реакция системы на предъявленную ситуацию запоминается и используется для организации контролируемых изменений динамических свойств системы управления. В зависимости от способов накопления опыта указанные системы разделяют на обучающиеся с поощрением и обучающиеся без поощрения (самоорганизующиеся) системы.
Зачастую используют комбинированные адаптивные системы управления, наделяемые полезными свойствами различных систем. Самонастраивающиеся системы Основная задача СНС – поддержание заданного в виде функционала I[x(t), e(t), y(t), u(t), f(t), t] меры качества системы вблизи экстремума при изменениях в процессе функционирования системы входных управляющих воздействий x(t), возмущающих воздействий f(t), а также динамических характеристик объекта. Значение функционала I изменяется, поэтому необходимо определить условия экстремума. Если I изменяется сравнительно медленно, целесообразно применять для определения экстремума поисковые методы. В беспоисковых системах используют, как правило, аналитические методы определения указанных условий. Беспоисковые системы обладают большим быстродействием, но требуют более полной информации об управляемом объекте. Все методы поиска экстремума подразделяются на регулярные и случайные. В регулярных методах поиска выбор направления поискового движения осуществляется по заранее заданному закону, а в случайных методах направление к экстремуму определяется случайным образом. К регулярным методам поиска экстремума относятся: - сканирование; - метод Гаусса-Зайделя (пошагового спуска); - метод градиента; - метод найскорейшего спуска; - методы экстраполяционного поиска; К случайным методам поиска относятся: - локальный случайный поиск с возвратом; - локальный случайный поиск с пересчетом; - локальный случайный поиск по наилучшей пробе; - локальный случайный поиск по статистическому градиенту; - глобальный случайный поиск с независимым выбором плотности распределения пробных шагов;
Рис. 2.2. Функциональная схема СНС: р – регулятор, О – объем управления, КС – контур самонастройки
Регулярные методы поиска экстремума Сканирование – полный перебор в допустимой области изменения управляемого параметра. Априорная информация – наличие свойства экстремальности у I(x) и необходимости соблюсти условие I(x*) £ I(x), где I(x*) – значение функционала качества в точке экстремума x*. Если обозначить допустимый интервал изменения параметра x через A, а заданную погрешность достижения экстремума – через e > 0, то в результате сканирования определяют n значений функционала качества в точках x1, x2,…,xn: I(x1), I(x2),…, I(xn), где После перебора всех значений I(xi) выбирают экстремальное значение. I(x*)=extr{ I(xi) }, i=1,n. Длительность процедуры поиска зависит от задаваемой погрешности e (т.е. от числа точек измерений значений I(xi)). Используют два способа обхода точек: строчная и спиральная развертка. Метод Гаусса-Зайделя. В этом методе не используется дополнительная информация о виде функционала качества I(x), в частности, предполагают, что I(x) является унимодальной функцией, имеющей один экстремум. Условие унимодальности можно записать следующим образом (для поиска минимума):
где xmin – положение минимума; x1, x2 – произвольные положения относительно точки минимума. Условие унимодальности значительно сокращает число просматриваемых точек по сравнению с полным перебором. В основу метода поиска положено исследование полного функционала
где ali – коэффициенты, характеризующие отклонение от экстремума. Отсюда
В точке экстремума xi = xiextr имеем
В методе Гаусса-Зайделя производится поочередное изменение координат x1, x2,…,xn и определяются частные экстремумы Недостатком метода является произвольность в выборе нумерации координат, что может в отдельных случаях существенно удлинить поиск. Метод градиента. Градиентом выпуклой дифференцируемой функции I(x1, x2,…) называют вектор, проекции которого на оси координат x1, x2,… соответственно равны частным производным Каждая из составляющих градиента может быть определена приближенно по двум замерам значений функции I(x) в близких точках x+D, т.е.: grad I(x) = [ I(x+D) - I(x-D)]/(2D). Если функция I(x) зависит от нескольких переменных, т.е. I(x1,x2,…,xn), градиент определяют по всем переменным:
После определения направления градиента осуществляют переход в новое положение по каждой координате в зависимости от максимальной величины и направления градиента. В методе градиента используют свойство уменьшения его величины по мере приближения к экстремуму (рис. 3).
Рис. 2.3. Уменьшение градиента по мере приближения к экстремуму
Координаты каждого последующего положения определяют таким образом:
Следовательно, в методе градиента процесс поиска разделяется на два этапа. В начале делают пробный шаг для определения величины и направления градиента в соответствии с алгоритмом: xi = x0 + gDi, i = 1,n,(2.7) где x0 – координата вектора начального состояния; xi – координата вектора пробного состояния; g – величина пробного шага; Di – единичный вектор отклонения по заданной координате. Затем осуществляют одновременное рабочее смещение в направлении градиента всех координат в соответствии с уравнением
где x – вектор нового рабочего состояния; a – величина рабочего шага. Для ускорения поиска пробные и рабочие шаги зачастую совмещают. При наличии у функции качества «оврагов» или «гребней» движение по градиенту может стать очень извилистым. Кроме того, направление градиента зависит от выбранных масштабов изменения координат по каждой оси, т.е. при неблагоприятных масштабах по осям поиск может значительно затянуться.
Метод наискорейшего спуска. Является модификацией метода градиентного поиска. Здесь также определяют градиент в исходной точке, а затем движение происходит по выбранному направлению (A, B,..) до тех пор, пока функция качества продолжает уменьшаться. Затем вновь определяют направление градиента и организуется прямолинейное движение в этом направлении до уменьшения функции качества и получения минимального значения ее по данному направлению. Этот метод значительно сокращает процедуру поиска экстремума по сравнению с методом градиента, поскольку в нем уменьшается количество точек, в которых определяются направление и градиент. Методы экстраполяционного поиска Эти методы строятся на базе двух предположений: - либо заранее известно значение экстремума функции качества; - либо функция I(x) может быть приближенно представлена какой-нибудь известной функциональной зависимостью. В простейших случаях функцию качества заменяют кусочно-линейной функцией или квадратичной параболой. В случае линейной экстраполяции по двум замерам I(x0+D) и I(x0-D) истинному значению экстремума Iextr определяют положение точки экстремума x1, т.е. x1 = x0 + D+D[ Iextr – I(x0+D) / [ I(x0+D)-I(x0-D) ]. (2.9) Проверка истинности полученного положения экстремума осуществляется с помощью равенства I(x1) = Iextr. (2.10) При невыполнении равенства (2.10) процедура линейной экстраполяции повторяется, но для замеров (x1 ±-D1). В случае квадратичной экстраполяции по трем замерам функции качества I1 = I(x0-D), I2 = I(x0), I3 = I(x0-D), записывают три уравнения второго порядка
Решая систему уравнений (2.11), находят значения коэффициентов a, b, c:
Учитывая, что минимум параболы I’ = ax2+bx+c расположен в точке xmin= - b2/(4a) и равен Imin= c - b2/(4a), можно получить величину шага для смещения в экстремум x1 - x0 = (D/2)(I3 – I1)/(I1 – 2I2+I3)(I3 ), (2.13) и величину предполагаемого экстремума: Imin = I2 – (I3 – I2)2 / [ 8(I1 – 2I2+I3) ]. (2.14) Сравнивая действительное значение функции качества в точке I(x) с предполагаемым минимумом из (2.14), можно судить о близости к действительному экстремуму. Поиск заканчивается при совпадении с данной погрешностью e. Регулярные методы поиска экстремума, кроме полного перебора, имеют недостаток: при наличии у функции качества нескольких экстремумов, один из которых глобальный, поиск может заканчиваться в окрестности локального экстремума. Методы случайного поиска. В основу метода случайного поиска положен метод проб и ошибок, в соответствии с которым удачно найденное решение принимается, а неудачное – отвергается. Метод применяют для поиска локального и глобального экстремумов. Наилучший результат дают комбинированные методы. Локальный случайный поиск с возвратом. В этом методе первоначально производится фиксированный шаг в случайно выбранном направлении. Если значение функции качества в новом состоянии I(x1+D) превышает исходное значение I(x1) или остается неизменным, т.е. случайный выбор оказался неудачным, то происходит возврат в начальное состояние x1, откуда осуществляется новый шаг в случайном направлении. Если значение I(x1+D) уменьшилось, то следующий шаг в случайном направлении делается уже из точки (x1+D).
Алгоритм поиска можно записать в следующем рекуррентном виде: xi+1 = xi+Dxi+1, (2.15) где a – величина шага смещения; Ei+1 – случайный единичный вектор; E = (e1, e2,…, en). Блок-схема алгоритма случайного поиска приведена на рис. 2.4
Рис. 2.4. Блок-схема алгоритма случайного поиска экстремума
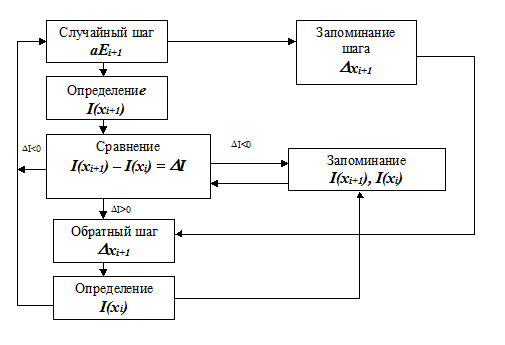
Алгоритм эффективен также в случае нестационарных функций качества, изменяющихся во времени по различным причинам. Локальный случайный поиск с пересчетом. Этот метод поиска отличается от предыдущего тем, что при неудачном шаге система не возвращается назад, а делает «пересчитанный» случайный шаг в новое состояние, при котором учитывается исходное состояние. Алгоритм поиска в рекуррентной форме:
где I*i = min I(xj)(j=1,2,…,i) – наименьшее значение функции качества за t предыдущих шагов поиска. Этот алгоритм используется в основном для случаев стационарной функции качества или при отсутствии помех. Поиск с пересчетом сокращает количество измерений функции качества. Блок-схема алгоритма поиска приведена на рис. 2.5. В процедуре поиска отсутствует определение I(xi) после неудачного поиска, а устройство памяти I(x) освобождается от дополнительной информации.
Рис. 2.5. Блок-схема алгоритма случайного поиска с пересчетом.
Локальный поиск по наилучшей пробе. Данный метод поиска содержит операцию накопления, состоящую из нескольких пробных шагов. По совокупности независимых проб принимается решение о выборе наиболее удачного состояния. Из исходного состояния xi делается m случайных пробных шагов aE1i+1, aE2i+1,…,aEmi+1. В полученных смещенных точках xji+1=xi+aEji+1, где j=1,m, производится вычисление значений функции качества I(xji+1) и запоминается состояние, которое привело к минимальному значению: I*(xji+1) = min I(xi+aEji+1), j=1,m. (2.17) Далее производится рабочий шаг в выбранном направлении: Dxi+1 = aE*i+1, (2.18) где E*i+1 – случайный единичный вектор наилучшей пробы. С увеличением числа пробных шагов m случайно выбранное направление приближается к направлению, обратному градиенту. Алгоритм (2.17) имеет недостаток, связанный с возможностью попадания в такую зону, когда рабочий шаг делается в сторону увеличения функции качества. Модификация этого метода осуществляется следующим образом:
В соответствии с (19) система сделает рабочий шаг вдоль наилучшей пробы только тогда, когда минимальное значение I*(xji+1) из всех проб не превышает исходного значения I(xi). Если это условие не выполняется, тогда повторяется цикл из m пробных шагов. Локальный случайный поиск по статическому градиенту. Этот метод используется в тех случаях, когда функцию качества I(x) нельзя представить в регулярном виде в условиях действия помех. По своей сути этот метод близок к методу стохастической аппроксимации. При наличии случайных параметров (e1,e2,…,en) регулярную функцию качества I(x) представим в виде случайной функции H(x, e) = H(x1, x2,…,xn, e1, e2,…, em), (2.20) где x=(x1, x2,…,xn)– вектор состояний поиска; e=(e1, e2,…,em) – вектор случайных помех. Зная вероятностные характеристики параметров (e1, e2,…,em), например плотность распределения r(e), можно усреднить функцию H(x, e) по этим параметрам и перейти вновь к усредненной регулярной функции качества
где Me – математическое ожидание. Из (2.21) можно сделать вывод, что получение функции качества в детерминированном виде связано с необходимостью вычисления интервала либо при жестких ограничениях на характер случайных воздействий e, либо при известных вероятностных характеристиках изменения таких воздействий. Однако обычно имеется информация об отдельных реализациях случайной функции H(x,e). При поиске экстремума дифференцируемой функции качества I(x) все n частных производных Grad I(x) = 0. (2.23) В результате замены I(x) на Me[H(x,e)] условия экстремума принимают следующий вид Grad Me[H(x,e)] = 0, (2.24) или, учитывая линейность операций, можно записать:
Осуществляя итеративную процедуру стохастической аппроксимации, определяют состояние X*, соответствующее экстремальному значению H*(x,e), постепенно приближаясь к нему: xi+1=xi–Aigrad H(xi, ei). (2.26) Таким образом, при отсутствии точного знания I(x) следует заменить ее стохастической оценкой H(x,e) и далее оперировать этой оценкой при поиске точки экстремума x*. Если H(x,e) представлена в виде скалярной функции скалярного аргумента X и случайного параметра e, процедура стохастической аппроксимации сводится к процедуре определения корня этой скалярной функции или к так называемой процедуре Роббинса-Монро. Пусть H(x,e) = L(x,e), (2.27) где L(x,e) – скалярная функция от параметра состояния x. Функцию L(x,e) можно представить в виде суммы регулярной составляющей f(x) и случайной составляющей e, причем M{e} = 0. В результате поиска определяет корень x* регулярной составляющей f(x), т.е. f(x*)=0, (2.28) в соответствии с процедурой xi+1=xi-aaL(Ei, xi ), (2.29) где a – знак наклона регулярной составляющей f(x) в точке x* (для минимума «+», для максимума «-»); a – постоянная, определяющая наклон аппроксимированной прямой к f(x). Если функция L(x, e) является однопараметрической функцией регрессии, задана своими реализациями H(xi, ei) и можно дать точечную оценку ее градиента
где Di – интервал оценки производной, то поиск экстремума сводится к поиску корня функции регрессии регулярной части L(x,e) в соответствии с процедурой Кифера-Вольфовица:
где В случайном поиске по статистическому градиенту из исходного состояния Xi делается m случайных шагов: DIj=Ij(xi+1)–I(xi). (2.32) После этого вычисляется вектор статистической оценки градиента в точке xi, т.е.
В пределе при
где a – величина рабочего шага. Таким образом, в случайном поиске по статистическому градиенту число точечных измерений статистической оценки градиента может быть меньше по сравнению с методами стохастической аппроксимации (m<n). Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов. Все рассмотренные способы поиска экстремума не пригодны для поиска глобального экстремума (кроме полного перебора) при многоэкстремальной функции качества. Методы поиска глобального экстремума базируются на статистических методах. Поиск статистическими методами позволяет управлять плотностью распределения независимых пробных шагов и сосредотачивать поисковые шаги в местах наиболее вероятного нахождения глобального экстремума. Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов может быть описан следующей рекуррентной формулой:
где x0i – это i -е пробное состояние, выбранное случайно и сохраненное в памяти в случае удачной пробы; I0(xi) - вычисленное в i -е -м пробном состоянии значение функции качества и сохраненное в памяти в случае удачной пробы; xi-1 – пробный шаг; I(xi) – значение функции качества на i -м пробном шаге. При равномерной плотности распределения пробных шагов поиск разделяется на K этапов из Nj пробных шагов, где j = 1,k. Каждый пробный шаг осуществляется внутри гиперпараллелепипеда в пространстве состояний X, т.е.
Причем стороны гиперпараллелепипеда с каждым j -м этапом уменьшаются в c > 1 раз по сравнению с (j-1) -м этапом в соответствии с формулами:
где xi(mj-1) – точка, соответствующая пробному шагу с наименьшим значением функции качества из всех проб на (j-1) -м этапе. Несмотря на равномерную плотность распределения пробных шагов внутри каждого этапа, происходит увеличение плотности распределения от этапа к этапу за счет уменьшения зоны поиска, т.е.
где Pj(x) – плотность распределения пробных шагов на j -м этапе;
Таким образом, на каждом пробном этапе осуществляются случайные пробные шаги, из которых выбирается шаг с наименьшим значением функции качества, а затем зона поиска сужается вокруг этой выбранной точки и снова производятся случайные пробные шаги до попадания в окрестность глобального экстремума. Иногда полезно пробные шаги на каждом последующем этапе распределять неравномерно, а по нормальному закону, например:
где s02 – исходная дисперсия, 0 <q <1. 2.4.1.Методы построения беспоисковых самонастраивающихся систем Такие системы обладают более высоким быстродействием, поскольку в них отсутствуют процессы поиска, замедляющие работу системы. Кроме того, поисковые движения создают заметные возмущения для работы основного контура. В беспоисковых системах используют несколько различных принципов аналитического определения условий экстремума, которые базируются на компенсационных подходах, например, принцип инвариантности или сравнения с эталоном-моделью, либо не идентификационных подходах, позволяющие определять связанные с функционалом качества параметры или характеристики управляемого процесса. Принцип инвариантности. Если в системе компенсируются возмущающие воздействия, то такая система становится инвариантной, т.е. независимой от этих воздействий. Так как в самонастраивающихся системах функция качества управления может изменяться под действием параметрических или внешних возмущений, то, компенсируя влияние этих возмущений, можно добиться стационарности функции качества и обеспечить работу системы в экстремальном режиме. Пусть система автоматического управления описывается уравнениями вида:
где x1,…,xn – регулируемые координаты; aji(p,t), bi(p,t) – дифференциальные операторы (полиномы от р) с переменными коэффициентами; fi(t) – внешние возмущения i=1, n, j=1, n или в более компактной форме
При действии параметрических возмущений происходит отклонение операторов системы от номинальных значений, равных aji(p,t) = a0ji(p), (2.42) на величины Daji(p,t) = aji(p,t) – a0ji(p). (2.43) Тогда (2.41) можно записать в виде:
Условие инвариантности любой из координат xi по отношению к некоторым из воздействий (параметрических и внешних), например, Daji(p,t) и fj определяется тождественным равенством нулю минора Dji определителя системы (2.44). В результате преобразований (2.44) это условие может быть записано так:
где cn+1(p,t), xn+1 – операторы и координаты компенсационного члена. Следовательно, для выполнения условия инвариантности (45) необходим второй канал для компенсации возмущений, с помощью которого обеспечивается равенство:
Операторы второго канала должны перестраиваться в зависимости от изменения операторов bj(p,t) и Daji(p,t). Принцип эталонной модели. Эффективным способом поддержания экстремального режима при функционировании самонастраивающейся системы является введение в контур самонастройки модели-эталона.
Сравнивая динамические процессы, происходящие в реальном объекте, с процессами модели, можно подстраивать характеристики системы управления таким образом, чтобы эти процессы достаточно близко совпадали. Этим обеспечивается функционирование реальной системы в экстремальном режиме (рис. 2.6). Пусть уравнение основного контура системы
где у – выходные координаты объекта;
f – возмущающее воздействие; A(p,t), B(p,t), C(p,t) – операторы. С учетом стационарного режима операторы
где
если объект соответствует минимально-фазовому звену. Уравнение для эталона-модели
Уравнение системы вместе с моделью
где B02(p), D(p,t) – операторы рассогласования в основном контуре; h – суммарный сигнал обратной связи в основном контуре; DM(p,t), DN(p,t) – отклонение от расчетного режима для операторов координаты у и возмущения f в обратной связи;
При выполнении условий
получим
Переходя от операторной формы к дифференциальной, получим
где e = у – уМ. Для асимптотического приближения к нулю рассогласования по регулируемой координате между основным контуром и моделью необходимо, чтобы параметрические рассогласования операторов в (54) были равны тождественно нулю, т.е.
Следовательно, для выполнения (55) необходимо синтезировать законы самонастройки:
Выбор Принципы определения градиента функции качества В беспоисковых системах градиент качества определяют без введения пробных воздействий. Однако отсутствие поисковых движений требует большого количества априорной информации. Такими сведениями могут быть зависимость функционала качества не только от рассогласования между математической моделью системы и реальной системой, но и от настраиваемых параметров контура самонастройки:
где e=М–У – рассогласование между моделью и системой; х – настраиваемые параметры. Для обеспечения экстремального значения J контур самонастройки должен перестраивать параметры х в направлении градиента
где Зная компоненты, можно перестраивать параметры х по закону
Компоненты градиента могут быть определены методом вспомогательного оператора. Пусть система состоит из объекта с передаточной функцией W0(p,a), где а – переменные параметры объекта, и регулятора с передаточной функцией Wрег(p,x), где х – настраиваемые параметры. Тогда выходная координата
Частная производная
В то же время из (58)
Таким образом, компоненты градиента функции качества определяют с помощью ошибки e и вспомогательного оператора Wвсп(p, x, a):
где Пример 2.1. Найти минимум функции качества
где а = const; a = 1.5. Поиск начинается из точки x1=3, x2=3. Для поиска экстремума используем метод Гаусса-Зайделя. Изменяем координату х1, оставив х2 постоянной. Тогда функция качества
Минимум J(x,3) находим
откуда первый экстремум х1=-2.25. Ему соответствует точка с координатами х1=-2.25, х2=3. Теперь оставим координату х1=-2.25 и будем изменять х2:
Данному экстремуму соответствует точка с координатами х1=-2.25; х2=1.7. Повторим цикл вычислений, закрепив х2=1.7
Пример 2.2. Найти минимум функции качества из примера 1 методом наискорейшего спуска из начальной точки с координатами В исходной точке частные производные
Двигаясь в направлении, обратном полученному градиенту, найдем координаты следующей точки (
а – пока неизвестный шаг перехода из точки ( Шаг определим, подставляя
или
Подставив аmax= 0.31, получим
Поступая аналогичным образом на второй итерац
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 829; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.28.79 (0.015 с.) |

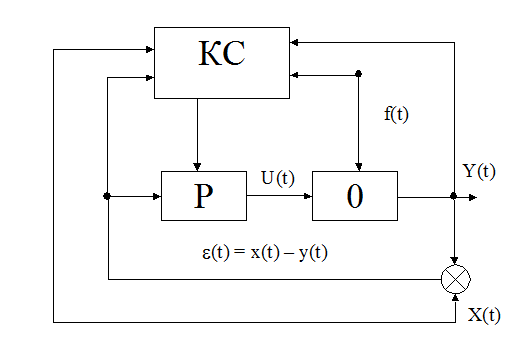
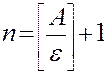 .
.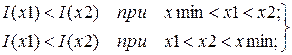 (2.1)
(2.1)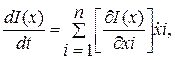 (2.2)
(2.2) ,
,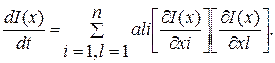 (2.3)
(2.3)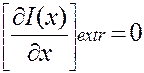 , поэтому во всех точках, кроме xiextr, функция (2.3) должна удовлетворять условию монотонного приближения к экстремуму.
, поэтому во всех точках, кроме xiextr, функция (2.3) должна удовлетворять условию монотонного приближения к экстремуму. (2.4)
(2.4) по каждой из координат, при этом все координаты, кроме выбранной, закрепляются. Взяв координату x1, при постоянных или нулевых значениях остальных координат отыскивают минимум
по каждой из координат, при этом все координаты, кроме выбранной, закрепляются. Взяв координату x1, при постоянных или нулевых значениях остальных координат отыскивают минимум  . После обращения в нуль
. После обращения в нуль 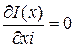 . Таким образом, находят частные экстремумы по всем n координатам. Затем осуществляют повторный цикл изменений, начиная с координаты x1, и так до тех пор, пока найденная точка экстремума не окажется экстремальной для всех координат.
. Таким образом, находят частные экстремумы по всем n координатам. Затем осуществляют повторный цикл изменений, начиная с координаты x1, и так до тех пор, пока найденная точка экстремума не окажется экстремальной для всех координат. .
.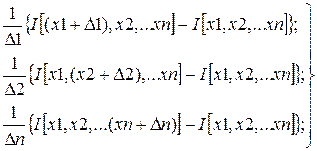 (2.5)
(2.5)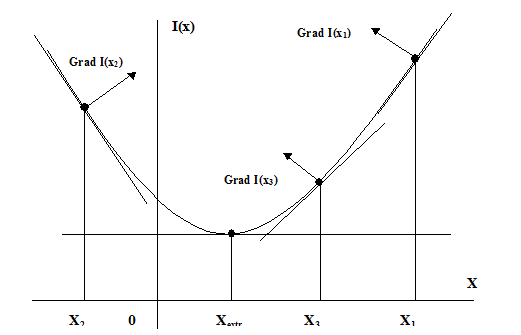
 (2.6)
(2.6)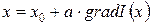 , (2.8)
, (2.8)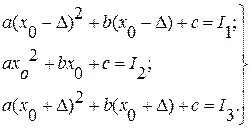 (2.11)
(2.11)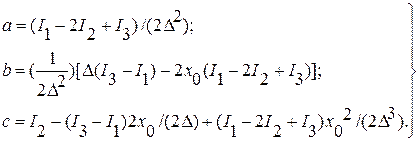 (2.12)
(2.12)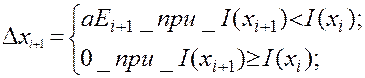
 (2.16)
(2.16)
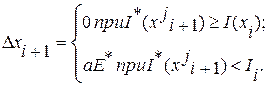 (2.19)
(2.19)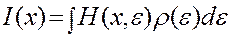 , (2.21)
, (2.21) (2.22)
(2.22) должны обращаться одновременно в нуль, т.е.
должны обращаться одновременно в нуль, т.е. . (2.25)
. (2.25) (2.30)
(2.30)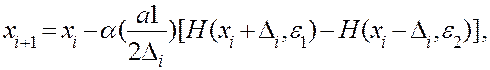 (2.31)
(2.31)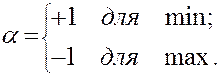
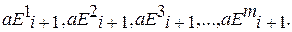 В новых точках
В новых точках  , вычисляют значения функции качества Ij(xj+1), j=1,m, и соответствующие приращения функции качества:
, вычисляют значения функции качества Ij(xj+1), j=1,m, и соответствующие приращения функции качества: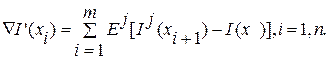 (2.33)
(2.33) при статистическая оценка совпадает с направлением градиента функции качества, поэтому рабочий шаг делается в направлении этой оценки
при статистическая оценка совпадает с направлением градиента функции качества, поэтому рабочий шаг делается в направлении этой оценки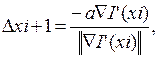 (2.34)
(2.34)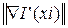 – норма вектора статистического градиента;
– норма вектора статистического градиента;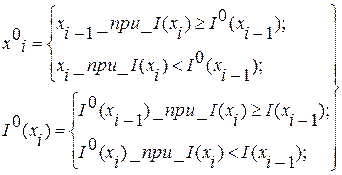 (2.35)
(2.35)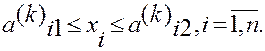 (2.36)
(2.36) (2.37)
(2.37)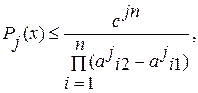 (2.38)
(2.38)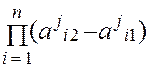 - объем гиперпараллелепипеда на j -м этапе.
- объем гиперпараллелепипеда на j -м этапе.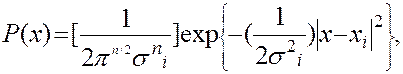 (2.39)
(2.39)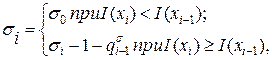
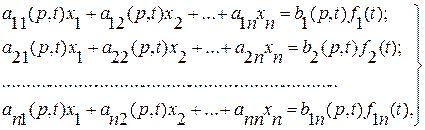 (2.40)
(2.40)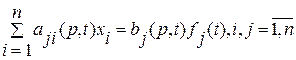 . (2.41)
. (2.41)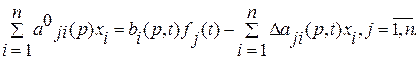 (2.44)
(2.44)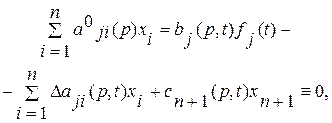 (2.45)
(2.45) (2.46)
(2.46)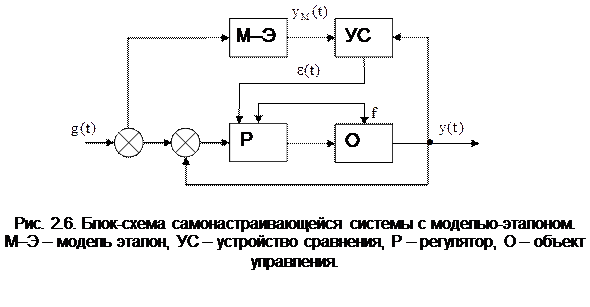
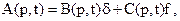 (2.47)
(2.47) – координата исполнительного механизма;
– координата исполнительного механизма;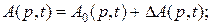
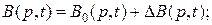 (2.48)
(2.48)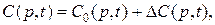
 – отклонения от расчетного стационарного режима. Уравнение объекта в расчетном режиме
– отклонения от расчетного стационарного режима. Уравнение объекта в расчетном режиме (2.49)
(2.49)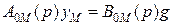 . (2.50)
. (2.50)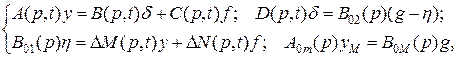 (2.51)
(2.51)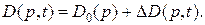
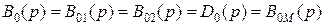 , (2.52)
, (2.52)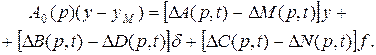 (2.53)
(2.53)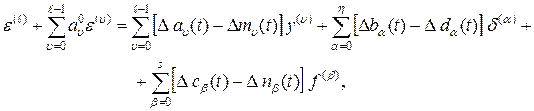 (2.54)
(2.54)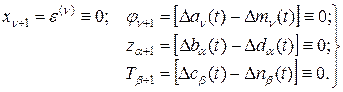 (2.55)
(2.55)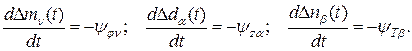 (2.56)
(2.56)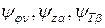 определяют методом Ляпунова.
определяют методом Ляпунова. (2.57)
(2.57)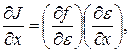 (2.58)
(2.58)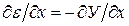 , поскольку математическая модель не зависит от настраиваемых параметров.
, поскольку математическая модель не зависит от настраиваемых параметров.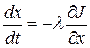 . (2.59)
. (2.59)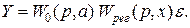 (2.60)
(2.60)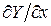 из (58)
из (58)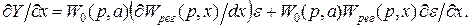 (2.61)
(2.61)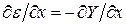 , поэтому, исключая
, поэтому, исключая  . (2.62)
. (2.62)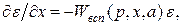 (2.63)
(2.63)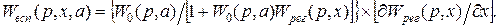
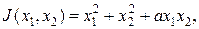
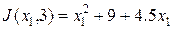 .
.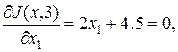



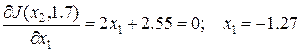 и т.д.
и т.д.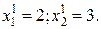
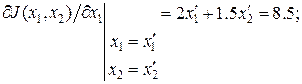

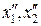 ):
):
 ) в точку (
) в точку (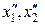 в выражение для функции качества
в выражение для функции качества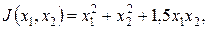 т.е.
т.е.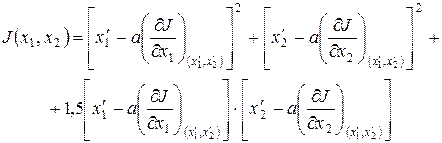 ,
,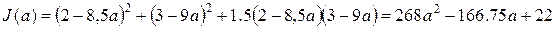
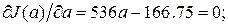 amax = 0.31.
amax = 0.31.




