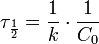Правило фаз для однокомпонентной системы

Для однокомпонентной системы (К=1) правило фаз записывается в виде

С = 3 – Ф

Если Ф=1, то С=2, говорят, что система бивариантна; Ф=2, то С =1, система моновариантна; Ф = 3, то С =0, система нонвариантна.

Соотношение между давлением (Р), температурой (Т) и объемом (V) фазы можно представить трехмерной фазовой диаграммой. Каждая точка (ее называют фигуративной) на такой диаграмме изображает некоторое равновесное состояние. Обычно удобнее работать с сечениями этой диаграммы плоскостью Р – Т (при V=const) или плоскостью Р – V (при T=const). Разберем более детально случай сечения плоскостью Р – Т (при V=const). В качестве примера рассмотрим фазовую диаграмму воды на рисунке 2.4.

Рис.2.4. Диаграмма состояния воды

Она составлена из 3 фазовых полей - областей различных (Р,Т) - значений, при которых вода существует в виде определенной фазы - льда, жидкой воды или пара. Эти фазовые поля разделены 3 граничными кривыми.

Кривая АВ - кривая испарения, выражает зависимость давления пара жидкой воды от температуры (или, наоборот, представляет зависимость температуры кипения воды от давления). Другими словами, эта линия отвечает двухфазному равновесию (жидкая вода) ↔ (пар), и число степеней свободы, рассчитанное по правилу фаз, составляет С = 3 – 2 = 1. Такое равновесие называют моновариантным. Это означает, что для полного описания системы достаточно определить только одну переменную - либо температуру, либо давление, так как для данной температуры существует только одно равновесное давление и для данного давления - только одна равновесная температура. При давлениях и температурах, соответствующих точкам ниже линии АВ, жидкость будет полностью испаряться, и эта область является областью пара. Для описания системы в данной однофазной области необходимы две независимые переменные (С = 3 – 1 = 2): температура и давление.

При давлениях и температурах, соответствующих точкам выше линии АВ, пар полностью сконденсирован в жидкость (С = 2). Верхний предел кривой испарения AB находится в точке В, которая называется критической точкой (для воды 374°С и 218 атм). Выше этой температуры фазы жидкости и пара становятся неразличимыми (исчезает четкая межфазная граница жидкость/пар), поэтому Ф=1.

Линия АБ - эта кривая возгонки льда (иногда ее называют линией сублимации), отражающая зависимость давления водяного пара надо льдом от температуры. Эта линия соответствует моновариантному равновесию (лед) ↔ (пар) (С=1). Выше линии АС лежит область льда, ниже - область пара.

Линия АГ - кривая плавления, выражает зависимость температуры плавления льда от давления и соответствует моновариантному равновесию (лед) ↔ (жидкая вода). Для большинства веществ линия АГ отклоняется от вертикали вправо, но поведение воды аномально: жидкая вода занимает меньший объем, чем лед. На основании принципа Ле Шателье можно предсказать, что повышение давления будет вызывать сдвиг равновесия в сторону образования жидкости, т.е. точка замерзания будет понижаться.

Исследования, проведенные Бриджменом для определения хода кривой плавления льда при высоких давлениях, показали, что существует семь различных кристаллических модификаций льда, каждая из которых, за исключением первой, плотнее воды.

Тройная точка воды А (точка, отражающая равновесие трех фаз - жидкости, льда и пара) в отсутствие воздуха находится при 0,0100°С и 4,6 мм рт.ст. Число степеней свободы С=3–3=0 и такое равновесие называют нонвариантным. В присутствии воздуха три фазы находятся в равновесии при 101,3 кПа (1 атм = 760 мм.рт.ст.) и при 0°С. Понижение тройной точки на воздухе вызвано следующим причинами:
1) растворимостью воздуха в жидкой воде при 1 атм, что приводит к снижению тройной точки на 0,0024°С;
2) увеличением давления от 4,6 мм рт.ст. до 1 атм, которое снижает тройную точку еще на 0,0075°С.

 

 

Вопрос17.

В физической химии системой называется тело или группа тел, выделенных из материального мира и имеющих определенные границы, которые отделяют их от окружающей среды. Системы могут быть гомогенными и гетерогенными. Система является гомогенной, если каждый параметр имеет во всех ее частях одинаковое значение или непрерывно изменяется от точки к точке. Например, вода дистиллированная (в каком7либо сосуде) — система гомогенная, так как в любой точке все свойства этой воды или одинаковы (плотность, удельная электропроводимость, теплопроводность и др.), или непрерывно изменяются от центра системы к ее границам (например, температура). К гомогенным системам относятся смеси газов, молекулярные и ионные растворы.

Гетерогенная система состоит из нескольких макроскопических частей, отделенных одна от другой видимыми поверхностями раздела. На этих поверхностях некоторые параметры изменяются скачком. Если создать насыщенный раствор какой-либо соли в воде, чему сопутствует наличие твердой соли на дне сосуда, то такая система "раствор + твердая соль" гетерогенна. В этом примере на границе раздела скачкообразно изменяются химический состав и плотность. Гомогенные части системы, отделенные от остальных частей видимыми поверхностями раздела, называются фазами. Например, совокупность кристаллов соли в насыщенном растворе составляет одну фазу, раствор над твердой солью — другую.

Состояние системы описывается совокупностью ее свойств (или свойств фаз) — температурой, давление, массой, плотностью, химическим составом, а также связями между изменениями этих свойств.

Каждое вещество, которое может быть выделено из системы и существовать вне ее, называется составляющим веществом. В водном растворе хлористого натрия составляющими веществами могут быть Н₂O и NaCl, но не ионы Na⁺ и Cl^-, так как они не могут существовать вне раствора.

Важная характеристика системы — число компонентов (k), под которым понимают наименьшее число составляющих веществ, с помощью которых можно описать состав каждой фазы системы в отдельности.

Если в системе не протекает химических реакций, число компонентов равно числу составляющих веществ. Например, в однофазной системе из газообразных гелия, водорода и аргона число компонентов равно числу составляющих веществ, т.е. трем, так как реакции между этими газами невозможны.

В системе, где составляющие вещества способны взаимодействовать друг с другом, число компонентов всегда меньше числа составляющих веществ. Например, водород и газообразный иод реагирует с образованием газообразного иодистого водорода. В этой системе

H₂(г) + I₂(г) = 2HL(г)

концентрации составляющих веществ при равновесии связаны уравнением

[HI]²/[H₂][I₂] = K,

где К — константа равновесия, имеющая определенное значение при заданной температуре. В этом случае для определения состава равновесной системы достаточно знать концентрации любых двух составляющих веществ, так как концентрация третьего определяется уравнением. Иными словами, система имеет два компонента. В общем случае число компонентов равно числу составляющих веществ минус число уравнений, связывающих концентрации этих веществ в равновесной системе.

Для описания системы необходим еще один параметр — число степеней свободы с, которое означает число независимых переменных (температура, давление, концентрация составляющих веществ), определяющих термодинамическое состояние равновесия системы. Значения этих переменных можно в известных пределах произвольно изменять, не меняя числа и вида фаз в системе. По числу степеней свободы системы называют инвариантными, у которых число степеней свободы равно нулю, моновариантными — с одной степенью свободы, бивариантными — с двумя и т.д.

В 1876 г. Гиббсом было сформулировано правило фаз, которое охватывает все случаи равновесия систем как гомогенных, так и гетерогенных. Это правило гласит: Число степеней свободы с равновесной термодинамической системы, на которую из внешних факторов влияют только давление и температура, равно числу компонентов системы k плюс 2 и минус число фаз f, т.е.

c = k + 2 - f

Нетрудно подсчитать, что для описанной выше газообразной смеси гелия, водорода и аргона число степеней свободы равно четырем, а для системы водород—газообразный иод—газообразный иодистый водород — трем.

Диаграмма состояния — наглядный способ представления областей существования различных фаз в зависимости от внешних условий, например от давления и температуры.

Диаграмма состояния воды — система с одним компонентом H₂O, поэтому наибольшее число фаз, которые одновременно могут находиться в равновесии, равно трем. Эти три фазы — жидкость, лед, пар. Число степеней свободы в этом случае равно нулю, т.е. нельзя изменить ни давление, ни температуру, чтобы не исчезла ни одна из фаз. Обычный лед, жидкая вода и водяной пар могут существовать в равновесии одновременно только при давлении 0,61 кПа и температуре 0,0075°С. Точка сосуществования трех фаз называется тройной точкой (O).

Кривая ОС разделяет области пара и жидкости и представляет собой зависимость давления насыщенного водяного пара от температуры. Кривая ОС показывает те взаимосвязанные значения температуры и давления, при которых жидкая вода и водяной пар находятся в равновесии друг с другом, поэтому она называется кривой равновесия жидкость—пар или кривой кипения.

Кривая ОВ отделяет область жидкости от области льда. Она является кривой равновесия твердое состояние—жидкость и называется кривой плавления. Эта кривая показывает те взаимосвязанные пары значений температуры и давления, при которых лед и жидкая вода находятся в равновесии.

Кривая OA называется кривой сублимации и показывает взаимосвязанные пары значений давления и температуры, при которых в равновесии находятся лед и водяной пар

Вопрос18.

Двойные системы. Состояние двойной системы определяется тремя независимыми параметрами - Т, р и содержанием х одного из компонентов, поэтому диаграмма состояния такой системы трехмерна. Обычно принимают постоянными Т или р и рассматривают соответствующие плоские сечения диаграммы состояния, называемые соотв. изотермич. (р — х)или изобарными (Т — х)диаграммами состояния. В конденсир. системах роль давления сравнительно невелика и в качестве параметров состояния обычно выбирают Т и состав (концентрацию одного из компонентов).
Д и а г р а м м ы п л а в к о с т и. Такие диаграммы состояния служат для установления условий равновесиямежду твердыми и жидкими фазами. Рассмотрим их осн. типы. Простейший вариант соответствует случаю, когда компоненты А и В образуют одну жидкую фазу (расплав или р-р), при охлаждении к-рой только выделяются (кристаллизуются) индивидуальные в-ва (не образуются ни твердые р-ры, ни хим. соед.).

Рис. 2. Диаграмма плавкости двойной системы, компоненты к-рой А и В не образуют твердых р-ров. L - область существования жидкости (расплава), (L + S_A) и (L + S_B) области сосуществования жидкой фазы и твердых А и В соотв.; (S_A + S_B) область существования мех. смеси твердых А и В. Т_АET_В и MEN - линии ликвидуса и солидуса соотв., E-эвтектич. точка. С, D, F, G, О и Q фигуративные точки (пояснения в тексте).

На диаграмме состояния (рис. 2) линия, изображающая зависимость от состава т-ры начала выделения из жидкой фазы твердого компонента (начала равновесной кристаллизации), наз. линией ликвидуса. Она состоит из двух ветвей Т_АЕ и Т_ВЕ, отграничивающих фазовое поле жидкости L от полей сосуществования жидкой фазы с твердыми А и В соотв. (поля L + S_A и L + S_B). Линия, изображающая зависимость от состава т-ры окончания равновесной кристаллизации при охлаждении (или начала плавления при нагр.), наз. линией солидуса. Ниже нее расположено фазовое поле S_A + S_B твердого состояния системы, отвечающее условиям сосуществования двух твердых фаз. Происходящие в системе фазовые изменения описываются след. образом. При охлаждении жидкой фазы, напр., из начального состояния С, фигуративная точка системы в целом движется вниз вдоль прямой CG. В точке ее пересечения с линией ликвидуса начинается кристаллизация компонента В, система становится двухфазной и дивариантной или, поскольку давление фиксировано, условно моновариантной. По мере кристаллизации В жидкость обогащается компонентом А, ее состав изменяется по ветви ликвидуса и по достижении системой состояния, изображаемого, напр., фигуративной точкой D, жидкой и твердой фазам соответствуют фигуративные точки О и Q. Прямые, соединяющие фигуративные точки двух находящихся вравновесии фаз, наз. нодами (или коннодами); горизонтальные ноды, подобные OQ, можно провести через любые точки фазовых полей, отвечающих гетерог. состояниям системы. При выражении состава в массовых (молярных) долях отношение отрезков OD и DQ пропорционально отношению масс (чисел молей) твердой и жидкой фаз (т. наз. правило рычага). Оно позволяет рассчитать по диаграмме состояния относительные кол-ва фаз при любой т-ре, чтобы, напр., определить полноту кристаллизации или степень извлечения данного компонента из жидкой фазы в твердую. В точке F пересечения прямой CG с линией солидуса начинаетсякристаллизация компонента А. Система становится трехфазной (жидкость и две твердые фазы А и В) и моновариантной (условно нонвариантной), т.е. при постоянном давлении совместная кристаллизация двух твердых фаз (т. наз. эвтектич. кристаллизация) протекает при постоянных т-ре и составе жидкой фазы, отвечающих координатам эвтектич. точки Е. После завершения эвтектич. кристаллизации система состоит из двух твердых фаз и является дивариантной (условно моновариантной). В обсуждаемом случае система после затвердевания состоит из относительно крупных кристаллов В и мелкодисперсной смеси совместно возникших при эвтектич. кристаллизации кристаллов А и В; такую смесь наз. эвтектикой. Если исходная жидкость имела эвтектич. состав, продукт ее затвердевания - мелкодисперсная эвтектика без примеси крупных кристаллов к.-л. из компонентов. При нагр. смеси твердых А и В описанные явления протекают в обратной последовательности: изотермич. образование жидкости эвтектич. состава вплоть до исчерпания к.-л. из твердых компонентов и растворение в жидкости оставшегося твердого компонента при дальнейшем повышении т-ры, к-рое завершается по достижении фигуративной точкой системы линии ликвидуса. Второй тип диаграммы характерен для случая ограниченной р-римости компонентов в твердом состоянии. Твердый р-р В в А (обозначается a-раствор) образуется лишь до определенной концентрации В, твердый р-р А в В (b-раствор) - лишь до определенной концентрации А. Для таких систем возможны два случая трехфазногоравновесия: 1) эвтектич. равновесие жидкого расплава состава Е, твердого р-ра a, концентрация к-рого соответствует точке М, и твердого р-ра b, концентрация к-рого соответствует точке N, при эвтектич. т-ре, к-рая, как правило, ниже т-р плавления T_A и Т_B обоих компонентов (рис. 3).

Рис. 3. Диаграмма плавкости двойной системы эвтектич. типа с ограниченными твердыми р-рами. L, a и b - области существования жидкой фазы (расплав) и твердых р-ров В в А и А в В соотв.; (L + a) и (L + b) - области сосуществования жидкой фазы и твердых р-ров a и b соотв.; (a + b) - область сосуществования двух твердых р-ров. Т_АЕТ_В и MEN - линии ликвидуса и солидуса соотв., E - эвтектич. точка.

При охлаждении затвердевшей смеси ниже линии солидуса MN происходит изменение концентраций твердых р-ров a и b соотв. по линиям MF и NG, к-рые дают температурную зависимость растворимости в твердом состоянии В в А и А в В. 2) Равновесие при т-ре Т_р, к-рая является промежуточной между т-рами плавления Т_Аи Т_B. Если, напр., т-ра начала кристаллизации расплава с высоким содержанием А выше Т_А (рис. 4), а с высоким содержанием В - ниже Т_B, линия ликвидуса состоит из двух ветвей Т_АР и Т_ВР, соответствующихкристаллизации твердых р-ров a и b.

Рис. 4. Диаграмма плавкости двойной системы перитектич. типа. Р - перитектич. точка, остальные обозначения те же, что и на рис. 3.

Эти ветви пересекаются в т. наз. перитектич. точке Р - фигуративной точке жидкой фазы, к-рая может равновесно сосуществовать одновременно с двумя твердыми р-рами a и b, составы к-рых определяются точками М и N. Линия солидуса состоит из трех ветвей: Т_AМ, MN и NT_B. При охлаждении двухфазной системы (L + b) до перитектич. т-ры Т_р в системе появляется третья фаза - р-р a. При протекании перитектич. превращения (фазовой р-ции) жидкость (расплав) + твердый р-р b D твердый р-р a система моновариантна, или условно нонвариантна, т. е. при данном давлении равновесие возможно лишь при постоянных т-ре и составах каждой из фаз. Если после окончания перитектич. р-ции остается избыток жидкой фазы, система переходит в двухфазное поле (L + a). При дальнейшем охлаждении происходит кристаллизация твердого a-раствора. Послед. понижение т-ры (ниже линии МF) приводит к тому, что однородный твердый a-раствор становится неустойчивым и, распадаясь, выделяет нек-рое кол-во р-раствора, состав к-рого отвечает линии NG. Если после окончания перитектич. р-ции полностью исчезает жидкая фаза, система переходит в двухфазное поле a + b; по мере снижения т-ры составы a- и b-растворов изменяются в соответствии с ходом линий MF и NG. Возможны и др. трехфазные равновесия, напр., при наличии у одного из компонентов полиморфных модификаций, когда все три сосуществующие фазы являются твердыми. Полиморфная модификация g может участвовать в т. наз. эвтектоидном превращении g D a + b или в перитектоидном превращении g + a D b, в принципе аналогичных рассмотренным выше эвтектич. и перитектич. превращениям. При метатектическом превращении модификация g при охлаждении распадается на твердую и жидкую фазы: gD a + L. Третий тип диаграммы описывает состояния двойной системы, компоненты к-рой А и В образуют устойчивое хим. соед., к-рое не разлагается вплоть до т-ры плавления и переходит в жидкую фазу того же состава, т. е. плавится конгруэнтно.

Рис. 5. Диаграмма плавкости двойной системы, компоненты к-рой А и В образуют конгруэнтно плавящееся хим. соед. А_mВ_n. D - сингулярный максимум, Е₁ и Е₂ - эвтектич. точки; остальные обозначения те же, что и на рис. 3 и 4.

В точке плавления, соответствующей стехиометрич. составу А_mВ_n, на линии ликвидуса имеется сингулярный максимум (рис. 5); это значит, что линия D - А_mВ_n разделяет систему на две подсистемы. На диаграмме максимуму отвечает излом (показан пунктиром на рис. 5). В каждой из подсистем взаимод. между компонентами, соотв. А и А_mВ_n, В и А_mВ_n, может быть представлено диаграммами эвтектич. или перитектич. (или любого другого) типа. Если соед. A_mB_n частично диссоциировано в жидкой фазе, максимум на кривой ликвидуса несколько сглажен в соответствии со степенью диссоциации. Если соед. А_mВ_n диссоциирует и в твердом состоянии, то сглаженный максимум будет и на линии солидуса. Однако независимо от вида максимума, общий характер фазового равновесия в системе определяется характером взаимод. соед. А_mВ_n с компонентами А и В.

Рис. 6. Диаграмма плавкости двойной системы, компоненты к-рой А и В образуют инконгруэнтно плавящееся хим. соед. А_mВ_n, обозначения те же. что и на рис. 4 и 5.

Четвертый тип диаграмм. Компоненты А и В образуют хим. соед., разлагающееся ниже т-ры плавления (т. наз. инконгруэнтное плавление). Напр., при охлаждении жидкости (расплава) до нек-рой т-ры Т_р (рис. 6) кристаллизуется только компонент В; при Т_р происходит перитектич. р-ция с образованием хим. соед. А_mВ_n в твердом состоянии, т. е. р-ция твердая фаза S_В + расплав перитектич. состава D твердая фаза S_А(m)В(n). Если при этом в твердой фазе компонент В имеется в избытке, в результате перитектич. р-ции исчезает жидкая фаза и при дальнейшем охлаждении ниже Т_р остается смесь двух твердых фаз S_B и S_А(m)B(n). Если же в твердой фазе компонента В недостает, в результате р-ции исчезают кристаллы В и жидкость при дальнейшем охлаждении выделяет кристаллы соед. А_mВ_n, изменяя свой состав по линии ликвидуса РЕ. При т-ре Т_Епроисходит эвтектич. кристаллизация A_mB_n и А. Возможны и др. варианты диаграммы. Описанные типыдиаграмм плавкости могут усложняться из-за полиморфизма как компонентов А и В, так и соед. А_mВ_n.
Диаграммы растворимости. При отсутствии в системе твердых фаз диаграмма состояния состоит из области существования одной жидкой фазы (т. наз. области гомогенности) и области сосуществования двух насыщенных жидких р-ров разного состава, образующих несмешивающиеся друг с другом слои (рис. 7). Кривая, разделяющая эти области, наз. бинодалью. Так, при т-ре Т₁ в равновесии находятся р-р компонента В в А (его состав отвечает точке С) и р-р А в В (его состав отвечает точке D). Если однородный р-р 1 охладить до т-ры Т₁, он распадется на две жидкие фазы.

Рис. 7 Диаграмма растворимости двойной системы, компоненты к-рой А и В ограниченно растворимы друг в друге; 1 область существования однородного р-ра, 2 область сосуществования двух насыщенных р-ров; ECKDF - бинодаль, CD - нода, К -верхняя критич. точка растворимости.

Обычно при повышении т-ры взаимная растворимость жидкостей увеличивается, поэтому по своим св-вам оба насыщенных р-ра, составы к-рых изменяются по отрезкам бинодали ЕК и KF, сближаются. Наконец, при т-ре T_к различие между ними исчезает; эта т-ра наз. критической т-рой растворимости (смешения), выше нее может существовать лишь одна жидкая фаза. Большинство систем с расслоением р-ров характеризуются только одной критич. т-рой р-римости, чаще всего верхней, т. е. на диаграмме состояния имеют незамкнутую снизу бинодаль. Если в таких системах не образуются хим. соед., область сосуществования двух жидких фаз ограничена снизу кривой кристаллизации одного из компонентов при т-ре превращения жидкая фаза 1 Dжидкая фаза 2 + твердая фаза. Такое трехфазное равновесие наз. монотектическим; оно по своей термодинамич. природе аналогично эвтектическому или эвтектоидному. При синтектическом трехфазномравновесии две жидкие фазы взаимодействуют с образованием твердого соед. Такое равновесие аналогично перитектическому. В нек-рых системах бинодаль имеет форму замкнутой кривой (овал), т. е. система имеет две т-ры смешения верхнюю и нижнюю. Диаграмма равновесия жидкость-пар. При р = const каждому составужидкой смеси отвечает определенная т-ра равновесия с паром и определенный состав пара, отличающийся, как правило, от состава жидкой смеси. На диаграмме состояния (рис. 8, а) кривые кипения и конденсацииизображают зависимости т-р начала кипения и конденсации от состава и отделяют поля жидкости L и пара V от поля (L + V)гетерог. состояний жидкость-пар. На кривой кипения м. б. экстремум: максимум (рис. 8, б) или минимум (рис. 8, в); в этих точках кривая кипения касается кривой конденсации, т. е. составы равновесныхжидкости и пара совпадают Жидкие смеси такого состава полностью выкипают, подобно чистым жидкостям, при постоянной т-ре без изменения состава (см. Азеотропные смеси). Диаграммы состояния, описывающиеравновесия двухкомпонентных твердых р-ров с жидкими р-рами и жидких р-ров с паром, подобны.

Рис. 8. Диаграммы состояния, двойной системы, описывающие равновесие жидкость - пар. L и V области существования жидкости и пара соотв.. (L + V) область сосуществования жидкой и паровой фаз; а система без азеотропной точки; б и в два типа азеотропных смесей.

 

Вопрос19.

Законы химической термодинамики позволяют определить направление и предел протекания возможного при данных условиях химического процесса, а также его энергетический эффект. Однако термодинамика не может ответить на вопросы о том, как осуществляется данный процесс и с какой скоростью. Эти вопросы – механизм и скорость химической реакции – и являются предметом химической кинетики.

СКОРОСТЬ ХИМИЧЕСКОЙ РЕАКЦИИ

Дадим определение основному понятию химической кинетики – скорости химической реакции:

Скорость химической реакции есть число элементарных актов химической реакции, происходящих в единицу времени в единице объема (для гомогенных реакций) или на единице поверхности (для гетерогенных реакций).

Скорость химической реакции есть изменение концентрации реагирующих веществ в единицу времени.

Первое определение является наиболее строгим; из него следует, что скорость химической реакции можно также выражать как изменение во времени любого параметра состояния системы, зависящего от числа частиц какого-либо реагирующего вещества, отнесенное к единице объема или поверхности – электропроводности, оптической плотности, диэлектрической проницаемости и т.д. и т.п. Однако наиболее часто в химии рассматривается зависимость концентрации реагентов от времени. В случае односторонних (необратимых) химических реакций (здесь и далее рассматриваются только односторонние реакции) очевидно, что концентрации исходных веществ во времени постоянно уменьшаются (ΔС_исх < 0), а концентрации продуктов реакции увеличиваются (ΔС_прод > 0). Скорость реакции считается положительной, поэтому математически определение средней скорости реакции в интервале времени Δt записывается следующим образом:

(II.1)

В различных интервалах времени средняя скорость химической реакции имеет разные значения; истинная (мгновенная) скорость реакции определяется как производная от концентрации по времени:

(II.2)

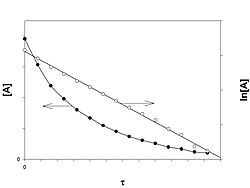
Графическое изображение зависимости концентрации реагентов от времени есть кинетическая кривая (рисунок 2.1).

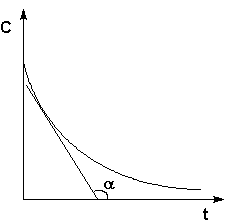
Рис. 2.1 Кинетические кривые для исходных веществ (А) и продуктов реакции (В).

Истинную скорость реакции можно определить графически, проведя касательную к кинетической кривой (рис. 2.2); истинная скорость реакции в данный момент времени равна по абсолютной величине тангенсу угла наклона касательной:

Рис. 2.2 Графическое определение V_ист.

(II.3)

Необходимо отметить, что в том случае, если стехиометрические коэффициенты в уравнении химической реакции неодинаковы, величина скорости реакции будет зависеть от того, изменение концентрации какого реагента определялось. Очевидно, что в реакции

2Н₂ + О₂ ––> 2Н₂О

концентрации водорода, кислорода и воды изменяются в различной степени:
ΔС(Н₂) = ΔС(Н₂О) = 2 ΔС(О₂).

Скорость химической реакции зависит от множества факторов: природы реагирующих веществ, их концентрации, температуры, природы растворителя и т.д.

Вопрос 20.

Порядок химической реакции

Порядок реакции по данному веществу — показатель степени при концентрации этого вещества в кинетическом уравнении реакции.

[править]Реакция нулевого порядка

График зависимости концентрации реагента A в реакции A → B от времени для нулевого порядка реакции

Кинетическое уравнение имеет следующий вид:

V ₀ = k ₀

Скорость реакции нулевого порядка постоянна во времени и не зависит от концентраций реагирующих веществ. Нулевой порядок характерен, например, для гетерогенных реакций в том случае, если скорость диффузии реагентов к поверхности раздела фаз меньше скорости их химического превращения.

[править]Реакция первого порядка

График зависимости концентрации реагента A для первого порядка реакции

Кинетическое уравнение реакции первого порядка:

Приведение уравнения к линейному виду даёт уравнение:

Константа скорости реакции вычисляется как тангенс угла наклона прямой к оси времени:

k ₁ = − tgα

Период полупревращения:

[править]Реакция второго порядка

График зависимости концентрации реагента A для второго порядка реакции

Для реакций второго порядка кинетическое уравнение имеет следующий вид:

или

В первом случае скорость реакции определяется уравнением

Линейная форма уравнения:

Константа скорости реакции равна тангенсу угла наклона прямой к оси времени:

k ₂ = − tgα

Во втором случае выражение для константы скорости реакции будет выглядеть так:

Период полупревращения (для случая равных начальных концентраций!):

[править]Молекулярность реакции

Молекулярность элементарной реакции — число частиц, которые, согласно экспериментально установленному механизму реакции, участвуют в элементарном акте химического взаимодействия.

Мономолекулярные реакции — реакции, в которых происходит химическое превращение одной молекулы (изомеризация, диссоциация и т. д.):

H₂S → H₂ + S

Бимолекулярные реакции — реакции, элементарный акт которых осуществляется при столкновении двух частиц (одинаковых или различных):

СН₃Вr + КОН → СН₃ОН + КВr

Тримолекулярные реакции — реакции, элементарный акт которых осуществляется при столкновении трех частиц:

О₂ + NО + NО → 2NО₂

Реакции с молекулярностью более трёх неизвестны.

Для элементарных реакций, проводимых при близких концентрациях исходных веществ, величины молекулярности и порядка реакции совпадают. Чётко определенной взаимосвязи между понятиями молекулярности и порядка реакции нет, так как порядок реакции характеризует кинетическое уравнение реакции, а молекулярность — механизм реакции. Закон действия масс

 

Закон действия масс открыт опытным путем К.М. Гульдбергом и П. Вааге в 1867 г. Он гласит: При постоянной температуре скорость химической реакции пропорциональна произведению концентраций реагирующих веществ, причем каждая концентрации входит в произведение в степени, равной коэффициенту, стоящему перед формулой вещества в уравнении реакции.

 

Уравнение химической реакции в общем виде можно представить так:

 

аА + вВ ↔ сС + dD

 

Тогда скорость реакции можно выразить уравнением:

 

V = k*[A]a *[B]b

 

Все химические реакции можно разделить на обратимые и необратимые реакции. Необратимые реакции протекают до конца – до полного израсходования одного из реагирующих веществ. Обратимые реакции протекают не до конца: ни одно из реагирующих веществ не расходуется полностью. Когда скорости прямой и обратной реакции становятся одинаковыми, наступает химическое равновесие. Количественной характеристикой химического равновесия служит константа химического равновесия.

 

Согласно закону действия масс, скорости прямой V1 и обратнойV2 реакции выражаются уравнениями:

 

V1= k1*[A]a *[B]b

 

V2= k2*[C]c *[D]d

 

При равновесии V1 = V2, значит, k1*[A]a *[B]b= k2*[C]c *[D]d

 

Отношение констант скорости прямой и обратной реакций есть величина постоянная. Она и называется константой химического равновесия

 

К = k1 / k2 K = (k2*[C]c *[D]d)/k1*[A]a *[B]b

 

Вопрос21.