Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
X. Кристаллизация растворов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Раствор, в отличие от чистой жидкости не отвердевает целиком при одной температуре. Кристаллы начинают выделяться при какой-то одной температуре. По мере понижения температуры количество их растет, пока весь раствор не отвердеет. Температурой начала кристаллизации называют температуру, при которой при охлаждении раствора начинается образование кристаллов. Не рассматривая здесь систем, в которых происходит образование твердых растворов, можно сказать, что температурой начала кристаллизации называется температура, при которой кристаллы растворителя находятся в равновесии с раствором данного вещества. Опыт показывает, что разбавленный раствор замерзает при температуре более низкой, чем чистый растворитель. Такое изменение температуры можно рассматривать как общее правило. Для характеристики температуры замерзания раствора введена величина “понижение температуры замерзания” DT 3. Она определена как разность между температурами замерзания чистого растворителя и раствора: DT3= Понижение температуры замерзания пропорционально концентрации растворенного вещества в растворе. DT=K*c Коэффициент K называется молярным понижением температуры замерзания или криоскопической постоянной. К =
lпл – удельная теплота плавления XI. Кипение растворов. Если рассматривать растворы нелетучего вещества в летучих растворителях, то температура кипения таких растворов всегда выше температуры кипения чистого растворителя. Повышение температуры кипения будет тем больше, чем выше концентрация раствора. И для разбавленных растворов его можно считать пропорциональным концентрации. Для растворов температуры кипения являются более высокими, чем для чистого растворителя и разность между ними DТкип = T кип - будет тем большей, чем выше концентрация растворов. Повышение температуры кипения пропорционально концентрации раствора. DT кип = Е*с Коэффициент пропорциональности Е является постоянной. Он называется молярным повышение температуры кипения или эбуллиоскопической постоянной. Е = lисп – удельная теплота его испарения.
Вопрос15 Осмос. Осмос-это самопроизвольный переход растворителя через полупроницаемую мембрану из разбавленного раствора или чистого растворителя в концентрированный раствор. Это явление можно продемонстрировать с помощью прибора, схематически изображенного на рис. 6.39. Широкий конец трубки, закрытый мембраной животного происхождения (например, бычьим пузырем), наполняют раствором сахара и погружают в стакан с водой. Через некоторое время вода переходит сквозь мембрану в раствор сахара. Мембрана, пропускающая частицы растворителя, но не пропускающая частицы растворенного вещества, называется полупроницаемой мембраной. Полупроницаемая мембрана пропускает частицы растворителя в обоих направлениях. Однако, поскольку с той стороны мембраны, где концентрация раствора выше, концентрация растворителя, наоборот, ниже, происходит результирующий переход растворителя в концентрированный раствор. Это приводит к установлению разности давлений по обе стороны мембраны. Давление, которое необходимо приложить к концентрированному раствору, чтобы воспрепятствовать переносу растворителя через мембрану, называется осмотическим давлением. Его обозначают греческой буквой п. Осмотическое давление является коллигативным свойством, поскольку оно зависит только от концентрации растворенных частиц, а не от их химического состава. Осмотическое давление играет важную роль в биологических процессах. Например, в организме животных некоторые типы клеток, например эритроциты, содержат солевой раствор. Эти клетки ограничены плазматической мембраной. В водной среде эритроциты подвергаются осмосу, набухают и лопаются. Однако, если они попадают в более концентрированный раствор соли, клетки сморщиваются.
Модули установки для получения сверхчистой воды на основе обратного осмоса. Такая вода необходима в полупроводниковой промышленности. Амеба-одноклеточное существо. Вода непрерывно поступает в ее тело благодаря осмосу. Растительные клетки содержат солевые растворы в особых полостях - вакуолях. Вакуоль окружена тонким слоем цитоплазмы, который обладает свойствами полупроницаемой мембраны и контролирует поглощение воды растительной клеткой. Если давление, приложенное к концентрированному раствору, превышает осмотическое давление, растворитель переходит из концентрированного раствора через мембрану в разбавленный раствор. Этот процесс называется обратный осмос. Он находит промышленное применение с целью получения питьевой воды из морской воды. Эксперименты, подобные описанному выше с сахарным раствором, показывают, что: 1) при постоянной температуре осмотическое давление прямо пропорционально разности концентраций в растворах, разделенных мембраной; 2) при фиксированной разности концентраций осмотическое давление прямо пропорционально абсолютной температуре. Соотношение между осмотическим давлением и температурой аналогично уравнению состояния идеального газа (см. разд. 3.1). Оно называется уравнением Вант-Гоффа:
В этом уравнении тс - осмотическое давление, К-объем раствора, и-число молей растворенного вещества, T-абсолютная температура, Л-молярная газовая постоянная. Уравнение (11) может быть представлено в другой форме:
Уравнение Вант-Гоффа является приближенным и справедливо только для разбавленных растворов. Определение относительной молекулярной массы растворенного вещества по осмотическому давлению раствора Уравнение Вант-Гоффа может использоваться для определения относительной молекулярной массы растворенного вещества по создаваемому им осмотическому давлению, которое устанавливают экспериментальным путем. Этот метод особенно удобен для определения средней относительной молекулярной массы полимеров и других макро-молекулярных веществ. Пример Раствор сахара с концентрацией 2,5 г/дм3 создает осмотическое давление 8,3 х х 104 атм при 25 °С. Вычислим относительную молекулярную массу растворенного вещества. Решение Искомое значение относительной молекулярной массы Мг растворенного вещества можно найти непосредственно с помощью уравнения Вант-Гоффа (11). Исходные данные задачи таковы:
Вопрос16 ФАЗОВЫЕ РАВНОВЕСИЯ Равновесие процесса перехода вещества из одной фазы в другую без изменения химического состава называется фазовым равновесием. Примерами фазовых равновесий являются следующие процессы:
Как и в случае химического равновесия, скорость прямого процесса равна скорости обратного процесса, а условие фазового равновесия ΔG = 0. Для фазового равновесия соблюдается принцип Ле Шателье. Так, при повышении температуры равновесие смещается в сторону эндотермического процесса, например плавления или испарения. С увеличением давления равновесие сдвигается в сторону процессов, при которых уменьшается объем, например, если газ превращается в жидкое или твердое состояние.
Правило фаз Правилу фаз уже более 100 лет; математически оно было сформулировано Гиббсом в 1876 году, но только в 1887 году, после работ Розебома, стала очевидной практическая применимость этого правила при изучении химических равновесий. Это правило является одним из общих законов химии и физики, определяющим возможность перехода вещества из одного фазового состояния в другое.
Основные понятия и определения Любая гетерогенная система состоит из отдельных гомогенных, физически или химически различных, механически отделимых друг от друга частей, называемых фазами. Например, насыщенный раствор хлорида натрия с кристаллами NaCl в осадке и водяным паром над раствором - это система, состоящая из 3 фаз: жидкого раствора, твердой соли и газообразной воды. Фазы могут иметь различный химический состав и физические свойства и могут быть разделены чисто механическими операциями: раствор можно отфильтровать от осадка, а пар собрать в любом свободном объеме системы. Фаза - это совокупность всех гомогенных частей гетерогенной системы, отделенная от других частей системы четкими поверхностями раздела (межфазными границами). Химический состав и свойства остаются постоянными внутри объема, занимаемого фазой. При переходе через межфазную границу состав и свойства меняются скачкообразно. Поскольку газы в подавляющем большинстве случаев полностью смешиваются друг с другом, в системе может быть только одна газовая фаза, но много твердых и жидких несмешивающихся фаз. Компонент - химически однородная составная часть вещества, которая может быть выведена из системы. Например водный раствор LiCl и KCl состоит из трех компонентов (LiCl, KCl и Н2О). Числом независимых компонентов - К, называется наименьшее число веществ, с помощью которых можно описать состав каждой фазы в системе в отдельности. Это определение легко применить, когда вещества не реагируют друг с другом. Так, смесь воды и этанола - двухкомпонентная система. Ситуация усложняется, когда химическая реакция приводит к равновесию между веществами в системе. Число независимых компонентов обычно меньше числа веществ, образующих систему, потому что при равновесии концентрации различных веществ связаны определенными соотношениями. Существуют два типа уравнений связи: · уравнения химического равновесия, · дополнительные условия, которые связывают концентрации веществ или состав фаз. Каждая химическая реакция, каждое дополнительное условие уменьшают число независимых компонентов на 1. Таким образом, число независимых компонентов К выражается формулой: К = s – n – m где s - число веществ, n - число независимых химических реакций, m - число соотношений между концентрациями веществ или составами фаз. Приведем другой метод определения числа независимых компонентов. Пусть имеется система из нескольких фаз в равновесии, и пусть химическим анализом определен состав каждой фазы. Если все фазы имеют одинаковый состав, то система состоит только из одного компонента. Если две фазы взаимодействуют друг с другом с образованием третьей фазы, то имеется система из двух независимых компонентов; если необходимы три фазы, чтобы дать состав четвертой - то в системе три компонента и т.д. Выбор независимых компонентов зачастую произволен, но число компонентов К - величина фиксированная, она является важной характеристикой системы при данных условиях.
Пример 1. Твердый оксид кальция, твердый карбонат кальция и газообразный диоксид углерода находятся в равновесии. Общее число веществ s=3. Число независимых компонентов уменьшается на единицу (т.е. К=s–n=3–1=2), благодаря наличию химического равновесия, в котором участвуют три фазы: CaCO3(к) ↔ CaO(к) + CO2(г). Равновесие описывается следующей константой: Kp = рСО2 • aCaO / a СаСО3 = рСО2, так как активности твердых веществ равны единице (CaCO3 и CaO нерастворимы друг в друге). Данная константа не зависит от количеств карбоната и оксида кальция, принимающих участие в равновесии. Следовательно, система остается двухкомпонентной и в том случае, когда СаО и СО2 получаются при диссоциации СаСО3. Эти рассуждения будут справедливы для разложения любого твердого вещества с образованием газообразной и твердой фазы другого состава. Карбонат кальция представляет пример вещества, которое испаряется с разложением, или инконгруэнтно. В данном случае вполне естественно в качестве независимых компонентов выбрать СаО и СО2. Возможны и другие пары компонентов: СаСО3и СаО, СаСО3 и СО2.
Пример 2. Водород и кислород находятся в равновесии с водяным паром (s=3, n=1). В этой однофазной системе существует два независимых компонента (H2O и O2, H2O и H2 или H2 и O2), потому что состав третьего определяется из уравнения равновесия: 2 H2O(г) ↔ 2 H2(г) + O2(г). Если указаны дополнительные условия, то число независимых компонентов уменьшается до единицы (K=s–n–m=3–1–1=1). Например, если водород и кислород образуются только из воды, то имеется еще одно дополнительное уравнение связи р(Н2) = 2р(О2) (m=1), которое отражает равновесный состав газовой смеси.
Пример 3. При нагревании хлорид аммония диссоциирует на аммиак и хлороводород. В этой системе 2 фазы (твердая - хлорид аммония, и газообразная - смесь аммиака и хлороводорода) и 3 вещества (s=3), но только количество одного из них изменяется независимо. Химическое равновесие (n=1): NH4Cl(к) ↔ NH3(г) + HСl(г), с учетом того, что количество вещества твердой фазы определяет количество вещества в газообразной фазе (m=1), позволяет выбрать одно вещество - NH4Cl, для описания составов обеих фаз (K=s–n–m=3–1–1=1). Если к газовой фазе добавить один из продуктов диссоциации, например HCl, то система станет двухкомпонентной, поскольку состав твердой фазы как и прежде - NH3: HCl = 1: 1, а в газовой фазе NH3: HCl = x: y (s=3, n=1, m=0). Для выражения состава газовой фазы теперь нужно использовать два компонента - NH3 и HCl. Эти рассуждения справедливы для разложения любого вещества с образованием только газовой фазы (т.е. для вещества, которое возгоняется при нагревании). О таких веществах говорят, что они испаряются конгруэнтно. Еще один вид ограничений связан с ионными растворами.
Задача 1. Сколько независимых компонентов содержится в системе NaCl • H2O? Решение: Первый ответ - два: соль и вода. Второй - три: катион, анион и вода. Ошибка второго ответа заключается в следующем: в нем не учитывается электронейтральность раствора; раствор не может иметь заряда, поэтому число ионов Na+должно быть равно числу ионов Cl–. Т.е., s=3, но m=1 (условие электронейтральности раствора [Na+] = [Cl–]) и, следовательно, К=2. Такой же результат будет получен, если принимать во внимание диссоциацию воды. Числом степеней свободы - С, называется наименьшее число независимых переменных системы (давление, температура и концентрации веществ в различных фазах), которые необходимо задать, чтобы полностью описать состояние системы. В 1876 г. Гиббс вывел простую формулу, связывающую число фаз, находящихся в равновесии, число компонентов и число степеней свободы системы. Правило фаз Гиббса: С + Ф = К + 2 Согласно этому правилу, чем больше компонентов в системе, тем больше степеней свободы; с другой стороны, чем больше фаз тем меньше переменных, необходимо определить для полного описания системы. · Для любой системы число фаз максимально, когда С=0. · Для однокомпонентной системы К=1 максимальное число фаз Ф=3. · Для двухкомпонентной системы К=2 максимальное число фаз Ф=4.
Пример 4. Рассмотрим систему, образованную CaCO3(к) и продуктами его разложения - CaO(к) и CO2(г). Данная система двухкомпонентна - К=2, независимо от относительных количеств составляющих ее веществ (см. Пример 1); в системе присутствуют три фазы (Ф=3): две твердых - CaCO3(к) и CaO(к), и одна газообразная - CO2(г). Согласно правилу фаз, число степеней свободы такой системы С=1. Это означает, что для описания состояния системы достаточно одного параметра. В качестве такового удобно выбрать температуру, тогда p(СО2) = f(T). Следовательно, давление углекислого газа в системе, содержащей карбонат кальция, оксид кальция и оксид углерода в равновесии, однозначно определяется температурой системы. При постоянной температуре это давление - фиксированная величина, его можно вычислить через константу равновесия, используя термодинамические функции веществ. В случае Т=const нужно заменить двойку в выражении правила фаз на единицу (С + Ф = К + 1), тогда получим, что число степеней свободы данной системы при постоянной температуре С=0. Приведенные выше рассуждения справедливы для любой двухкомпонентной системы, в которой находятся в равновесии три фазы, одна из которых - газообразная. При постоянной температуре давление газа в такой системе есть величина постоянная и не зависит от соотношения фаз.
Пример 5. Хлорид аммония в равновесии с продуктами его диссоциации представляет однокомпонентную систему (К=1, см. Пример 3) с двумя фазами (Ф=2): твердой - NH4Cl(к), и газообразной - смесь NH3(г) и HСl(г). Применив к данной системе правило фаз, получим число степеней свободы С=1. Это означает, что для описания химического равновесия в нашем случае достаточно одной переменной. Константа равновесия имеет вид: Kp = pNH3 pHCl = p2/4, поскольку pNH3 = pHCl = p/2 (p = pNH3 + pHCl - общее давление продуктов диссоциации). Таким образом, Кр = f(p,T), но только один из аргументов функции является независимым. Выбирая, как и в предыдущем примере, в качестве независимого параметра температуру, получим p=f(T), т.е. давление продуктов диссоциации в рассматриваемой системе однозначно определяется температурой. Добавление в систему одного из продуктов диссоциации, например, HСl(г), кардинально меняет ситуацию. Несмотря на то, что число фаз остается прежним - Ф=2, данную систему уже нельзя считать однокомпонентной, число компонентов становится равным К=2 (см. Пример 3). Это приводит и к увеличению числа степеней свободы, теперь С=2. Выбирая в качестве таковых состав газовой фазы (х) и температуру (Т), получим p = f(x,T). Выбранные нами переменные однозначно определяют состояние данной системы. Зафиксировав температуру, мы уменьшим число степеней свободы до С=1. Это означает, что из двух оставшихся переменных - р, х, только одна является независимой, т.е. p = f(x). Полученный нами вывод проливает свет на один замечательный экспериментальный факт: добавление одного из продуктов диссоциации, например HCl, к системе, содержащей твердый NH4Cl и продукты его испарения, при постоянной температуре, изменяет общее давление в системе. Это не так в случае системы из CaCO3, CaO и CO2 при постоянной температуре, которая рассматривалась в предыдущем примере. Добавление избытка СО2 приводит к реакции его с оксидом кальция с образованием СаСО3, и давление в системе (определяемое давлением СО2) возвращается к первоначальному значению.
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 1068; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 .
. , где
, где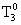 -температура замерзания растворителя
-температура замерзания растворителя
 , где
, где  - температура кипения чистого растворителя
- температура кипения чистого растворителя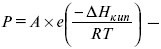 барометрическая формула Больцмана.
Следствия из закона Рауля:
1. Растворение нелетучего компонента в растворителе приводит к расширению температурной области существования жидкой фазы.
2. Понижение температуры замерзания и повышение температуры кипения прямо пропорциональны моляльной концентрации растворенного вещества.
3. Растворы, содержащие одинаковое число молей растворенных веществ в одинаковых молях растворителя, обнаруживают одно и то же понижение температуры замерзания и одно и то же повышение температуры кипения.
Δtкип=Э x Смоляльн,
где Э – эбуллиоскопическая константа, +0,52.
Δtзам=К x Смоляльн,
где К – криоскопическая константа, равная –1,86.
Эбуллиоскопическая константа
– разница между температурой кипения раствора и температурой чистого растворителя.
Криоскопическая константа
– разница между температурой замерзания раствора и температурой чистого растворителя.
Для решения задач об этих константах необходимо знать массу растворенного вещества и массу раствора. Например, масса хлороформа (трихлорметан CHCl3) рассчитывается по формуле:
барометрическая формула Больцмана.
Следствия из закона Рауля:
1. Растворение нелетучего компонента в растворителе приводит к расширению температурной области существования жидкой фазы.
2. Понижение температуры замерзания и повышение температуры кипения прямо пропорциональны моляльной концентрации растворенного вещества.
3. Растворы, содержащие одинаковое число молей растворенных веществ в одинаковых молях растворителя, обнаруживают одно и то же понижение температуры замерзания и одно и то же повышение температуры кипения.
Δtкип=Э x Смоляльн,
где Э – эбуллиоскопическая константа, +0,52.
Δtзам=К x Смоляльн,
где К – криоскопическая константа, равная –1,86.
Эбуллиоскопическая константа
– разница между температурой кипения раствора и температурой чистого растворителя.
Криоскопическая константа
– разница между температурой замерзания раствора и температурой чистого растворителя.
Для решения задач об этих константах необходимо знать массу растворенного вещества и массу раствора. Например, масса хлороформа (трихлорметан CHCl3) рассчитывается по формуле:  где m 1 – масса растворенного вещества;
m 2 – масса растворителя;
Δt – величина, показывающая на сколько градусов понизилась температура;
К – криоскопическая константа.
3.2.3 Температура кристаллизации разбавленных растворов
Раствор в отличие от чистой жидкости не отвердевает целиком при постоянной температуре; при некоторой температуре, называемой температурой начала кристаллизации, начинают выделяться кристаллы растворителя и по мере кристаллизации температура раствора понижается (поэтому под температурой замерзания раствора всегда понимают именно температуру начала кристаллизации). Замерзание растворов можно охарактеризовать величиной понижения температуры замерзания ΔТзам, равной разности между температурой замерзания чистого растворителя T°зам и температурой начала кристаллизации раствора Tзам:
где m 1 – масса растворенного вещества;
m 2 – масса растворителя;
Δt – величина, показывающая на сколько градусов понизилась температура;
К – криоскопическая константа.
3.2.3 Температура кристаллизации разбавленных растворов
Раствор в отличие от чистой жидкости не отвердевает целиком при постоянной температуре; при некоторой температуре, называемой температурой начала кристаллизации, начинают выделяться кристаллы растворителя и по мере кристаллизации температура раствора понижается (поэтому под температурой замерзания раствора всегда понимают именно температуру начала кристаллизации). Замерзание растворов можно охарактеризовать величиной понижения температуры замерзания ΔТзам, равной разности между температурой замерзания чистого растворителя T°зам и температурой начала кристаллизации раствора Tзам:
 (III.13)
Рассмотрим Р – T диаграмму состояния растворителя и растворов различной концентрации (рис. 3.5), на которой кривая ОF есть зависимость давления пара над твердым растворителем, а кривые ОА, ВС, DE – зависимости давления пара над чистым растворителем и растворами с возрастающими концентрациями соответственно. Кристаллы растворителя будут находиться в равновесии с раствором только тогда, когда давление насыщенного пара над кристаллами и над раствором одинаково. Поскольку давление пара растворителя над раствором всегда ниже, чем над чистым растворителем, температура, отвечающая этому условию, всегда будет более низкой, чем температура замерзания чистого растворителя. При этом понижение температуры замерзания раствора ΔTзам не зависит от природы растворенного вещества и определяется лишь соотношением числа частиц растворителя и растворенного вещества.
(III.13)
Рассмотрим Р – T диаграмму состояния растворителя и растворов различной концентрации (рис. 3.5), на которой кривая ОF есть зависимость давления пара над твердым растворителем, а кривые ОА, ВС, DE – зависимости давления пара над чистым растворителем и растворами с возрастающими концентрациями соответственно. Кристаллы растворителя будут находиться в равновесии с раствором только тогда, когда давление насыщенного пара над кристаллами и над раствором одинаково. Поскольку давление пара растворителя над раствором всегда ниже, чем над чистым растворителем, температура, отвечающая этому условию, всегда будет более низкой, чем температура замерзания чистого растворителя. При этом понижение температуры замерзания раствора ΔTзам не зависит от природы растворенного вещества и определяется лишь соотношением числа частиц растворителя и растворенного вещества.
 Рис. 3.5 Понижение температуры замерзания разбавленных растворов
Можно показать, что понижение температуры замерзания раствора ΔTзам прямо пропорционально моляльной концентрации раствора:
Рис. 3.5 Понижение температуры замерзания разбавленных растворов
Можно показать, что понижение температуры замерзания раствора ΔTзам прямо пропорционально моляльной концентрации раствора:
 (III.14)
Уравнение (III.14) называют вторым законом Рауля. Коэффициент пропорциональности K – криоскопическая постоянная растворителя – определяется природой растворителя.
3.2.4 Температура кипения разбавленных растворов
Температура кипения растворов нелетучего вещества всегда выше, чем температура кипения чистого растворителя при том же давлении. Рассмотрим Р – T диаграмму состояния растворителя и растворов различной концентрации (рис.3.5). Любая жидкость – растворитель или раствор – кипит при той температуре, при которой давление насыщенного пара становится равным внешнему давлению. Соответственно температуры, при которых изобара Р = 1 атм. пересечет кривые ОА, ВС и DE, представляющие собой зависимости давления пара над чистым растворителем и растворами с возрастающими концентрациями соответственно, будут температурами кипения этих жидкостей (рис. 3.6).
Повышение температуры кипения растворов нелетучих веществ ΔTк = Tк – T°кпропорционально понижению давления насыщенного пара и, следовательно, прямо пропорционально моляльной концентрации раствора. Коэффициент пропорциональности E есть эбулиоскопическая постоянная растворителя, не зависящая от природы растворенного вещества.
(III.14)
Уравнение (III.14) называют вторым законом Рауля. Коэффициент пропорциональности K – криоскопическая постоянная растворителя – определяется природой растворителя.
3.2.4 Температура кипения разбавленных растворов
Температура кипения растворов нелетучего вещества всегда выше, чем температура кипения чистого растворителя при том же давлении. Рассмотрим Р – T диаграмму состояния растворителя и растворов различной концентрации (рис.3.5). Любая жидкость – растворитель или раствор – кипит при той температуре, при которой давление насыщенного пара становится равным внешнему давлению. Соответственно температуры, при которых изобара Р = 1 атм. пересечет кривые ОА, ВС и DE, представляющие собой зависимости давления пара над чистым растворителем и растворами с возрастающими концентрациями соответственно, будут температурами кипения этих жидкостей (рис. 3.6).
Повышение температуры кипения растворов нелетучих веществ ΔTк = Tк – T°кпропорционально понижению давления насыщенного пара и, следовательно, прямо пропорционально моляльной концентрации раствора. Коэффициент пропорциональности E есть эбулиоскопическая постоянная растворителя, не зависящая от природы растворенного вещества.
 (III.15)
(III.15)
 Рис.3.6 Повышениетемпературыкипенияразбавленныхрастворов
Т.о., второй закон Рауля можно в наиболее общем виде сформулировать следующим образом:
Понижение температуры замерзания и повышение температуры кипения разбавленного раствора нелетучего вещества прямо пропорционально моляльной концентрации раствора и не зависит от природы растворенного вещества.
Второй закон Рауля является следствием из первого; данный закон справедлив только для бесконечно разбавленных растворов. Коэффициенты пропорциональности в уравнениях (III.14 – III.15) – эбулиоскопическая и криоскопическая константы – имеют физический смысл соответственно повышения температуры кипения и понижения температуры замерзания растворов с моляльной концентрацией, равной 1 моль/кг. Однако, поскольку такие растворы не являются бесконечно разбавленными, эбулиоскопическая и криоскопическая константы не могут быть непосредственно определены и относятся поэтому к числу т.н. экстраполяционных констант.
Рис.3.6 Повышениетемпературыкипенияразбавленныхрастворов
Т.о., второй закон Рауля можно в наиболее общем виде сформулировать следующим образом:
Понижение температуры замерзания и повышение температуры кипения разбавленного раствора нелетучего вещества прямо пропорционально моляльной концентрации раствора и не зависит от природы растворенного вещества.
Второй закон Рауля является следствием из первого; данный закон справедлив только для бесконечно разбавленных растворов. Коэффициенты пропорциональности в уравнениях (III.14 – III.15) – эбулиоскопическая и криоскопическая константы – имеют физический смысл соответственно повышения температуры кипения и понижения температуры замерзания растворов с моляльной концентрацией, равной 1 моль/кг. Однако, поскольку такие растворы не являются бесконечно разбавленными, эбулиоскопическая и криоскопическая константы не могут быть непосредственно определены и относятся поэтому к числу т.н. экстраполяционных констант.



 (11)
(11)