
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод исключения части неизвестных функций из системы ДУСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Основным методом решения систем вида (1) является метод исключения неизвестных функций, в результате которого система (1) сводится к одному ДУ n-го порядка относительно одной функции. Разберем принципиальное осуществление этого метода. Поставим задачу: исключить из системы (1) функций y2, y3, …, yn и получить ДУ относительно у1(х). 1 шаг: Дифференцируем первое уравнение системы (1) по х: здесь все функции, входящие в правую часть уравнения, выражаются через
2 шаг: продифференцируем ДУ (2) еще раз по х:
Проделав этап дифференцирования n раз, мы получим вместо системы (1) систему ДУ (2), (3) и т.д. Эта система имеет следующий вид: Из первых (n-1) уравнений этой последней системы можно алгебраически выразить набор из (n-1) штук функций подставив эти выражения у2, …, уn в последнее уравнение, получим ДУ n -го порядка относительно одной функции y1(x): При этом разрешение первых (n-1) уравнений относительно y2, y3, …, yn предполагается гипотетически, в общем случае ничем не обосновывается, но в каждом конкретном случае может подтверждаться практической реализацией. ПРИМЕР 1.Дана система двух ДУ РЕШЕНИЕ. Решение проводим методом повышения порядка ДУ за счет исключения из системы одной из неизвестных функций. Будем исключать у2(х), а у1(х) оставлять. 1 шаг: первое уравнение дифференцируем по х заменяем Так как в данной системе исключить нужно только одну функцию, то задача решается одним шагом. Чтобы закончить исключение у2 и в результате получить ДУ II порядка относительно у1, возьмем у2 из первого уравнения исходной системы и подставим в последнее ДУ II порядка: Получили ДУ II порядка относительно функции Запишем его в привычном виде «через штрихи» и решим известными методами:
ДУ(**) Общее решение ДУ (**): Вторую функцию Таким образом, получено решение исходной системы ДУ: ПРОВЕРКА. Продифференцируем полученные функции первое уравнение: второе уравнение: Задача Коши: Ответ: ЗАМЕЧАНИЯ. 1.Нормальная система ДУ вида (1) относительно n произвольных функций сводится методом исключения к одному ДУ n -го порядка, поэтому в общее решение системы должно войти ровно n произвольных постоянных, и для их нахождения нужно ставить n начальных условий 2. Если в систему ДУ входят производные высших порядков, то ее всегда можно привести к нормальной форме введением вспомогательных функций, а только после этого просчитать порядок того ДУ, к которому сведется система методом исключения, а следовательно, и количество произвольных постоянных. Пример 2.Рассмотрим механическое движение материальной точки ускорение равнодействующая сила Запишем уравнение движения в скалярной форме и получим систему дифференциальных уравнений относительно функций Сводим систему к нормальной форме с помощью вспомогательных функций Система в нормальной форме: Эта система сведется к ДУ VI порядка и в ее общее решение будет входить 6 произвольных констант (точнее, не более 6, так как иногда система n уравнений сводится к одному ДУ более низкого порядка, чем n; это бывает в случае, когда среди уравнений системы нет независимости и часть из них является следствием других уравнений). 3. При решении нормальных систем ДУ методом повышения порядка сохраняется тип ДУ исходной системы, в частности, гарантированно сохраняется линейность, то есть если все ДУ системы являются линейными, то и сведение будет к линейному ДУ. Также сохраняется постоянство коэффициентов и однородность или неоднородность ДУ. Это дает возможность отдельно построить теорию решения линейных систем с постоянными коэффициентами. Так можно рассмотреть нормальную систему линейных однородных ДУ с постоянными коэффициентами:
(в скобках написано выражение для случая неоднородных ДУ) неизвестные функции: Решение такой однородной системы (4) естественно искать в виде набора экспонент Здесь Подставив эти функции в систему (4), получим: Это система линейных алгебраических уравнений относительно Набор Для существования нетривиальных решений однородной системы необходимо и достаточно, чтобы главный определитель системы был равен 0, то есть Это равенство называется характеристическим уравнением для системы ДУ (4), оно является алгебраическим уравнением n -ной степени относительно числа k и, следовательно, имеет ровно n корней на множестве комплексных чисел С. Далее по корням характеристического уравнения разрабатывается теория записи общего решения системы, аналогичная правилу составления ФСЧР и общего решения линейного однородного ДУ с постоянными коэффициентами n -го порядка. 4. Система линейных ДУ с постоянными коэффициентами часто записывается и решается в матричном виде: (4) Характеристическое уравнение этой системы имеет вид 5. Понятие фазового пространства. Рассмотрим систему трех ДУ относительно трех функций Решение этой системы всегда можно трактовать как траекторию движения точки с координатами Аналогично решение системы относительно n неизвестных функций можно трактовать как уравнение линии (траектории движения) точки в пространстве R n, которое и называется фазовым пространством для данной системы ДУ. Такая трактовка дает возможность проиллюстрировать решения системы ДУ в виде некоторых линий в фазовом пространстве.
|
||||||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 726; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.64.113 (0.008 с.) |


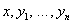 по равенствам (1), поэтому правую часть последнего уравнения можно обозначить одной ФНП
по равенствам (1), поэтому правую часть последнего уравнения можно обозначить одной ФНП 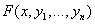 ; в результате получим, что
; в результате получим, что

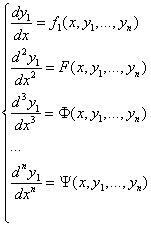
 через
через  ;
;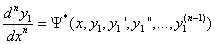
 и начальные условия
и начальные условия 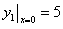 ,
, 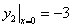 . Требуется найти функции у1(х) и у2(х).
. Требуется найти функции у1(х) и у2(х). ;
; на выражение, взятое из первого уравнения исходной системы,
на выражение, взятое из первого уравнения исходной системы, 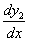 - на выражение, взятое из второго уравнения исходной системы:
- на выражение, взятое из второго уравнения исходной системы: .
.

 .
. – линейное, неоднородное, с постоянными коэффициентами.
– линейное, неоднородное, с постоянными коэффициентами.


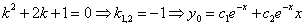 ;
;
 - подходит под I специальный вид, в котором
- подходит под I специальный вид, в котором 
 ;
;
 .
. .
. исходной системы найдем, используя первое уравнение этой системы и уже найденную функцию
исходной системы найдем, используя первое уравнение этой системы и уже найденную функцию 
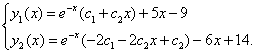



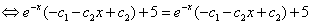 - верно;
- верно;

 - верно
- верно общее решение системы ДУ найдено верно.
общее решение системы ДУ найдено верно.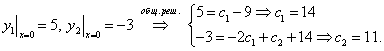
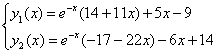 – это частное решение данной системы, удовлетворяющее поставленным начальным условиям.
– это частное решение данной системы, удовлетворяющее поставленным начальным условиям. , начальные условия
, начальные условия 
 ,
, ,
,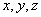 – координаты движущейся точки (функции от t, t-время),
– координаты движущейся точки (функции от t, t-время), .
. ,
, 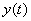 ,
,  :
:
 :
: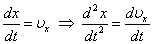 ,
, 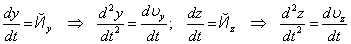 .
.

 ;
;  - числа или const по t, называются коэффициентами системы линейных ДУ.
- числа или const по t, называются коэффициентами системы линейных ДУ.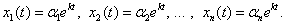
 - это числа, которые подбираются из условия, что все функции x1(t), x2(t), …, xn(t) удовлетворяют исходной системе ЛОДУ.
- это числа, которые подбираются из условия, что все функции x1(t), x2(t), …, xn(t) удовлетворяют исходной системе ЛОДУ.
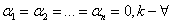 является тривиальным решением этой системы, но он приводит и к тривиальному решению системы ДУ
является тривиальным решением этой системы, но он приводит и к тривиальному решению системы ДУ  . Для нахождения нетривиальных решений запишем систему как однородную относительно
. Для нахождения нетривиальных решений запишем систему как однородную относительно  :
: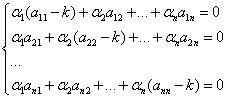
 .
. , где
, где 
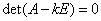 , где
, где  - это единичная матрица порядка n. Работа с системой (4) становится более компактной.
- это единичная матрица порядка n. Работа с системой (4) становится более компактной. , записанную в нормальной форме:
, записанную в нормальной форме: 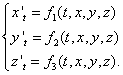
 является параметрическими уравнениями этой траектории движения.
является параметрическими уравнениями этой траектории движения.


