
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Физическая задача, приводящая к понятию дифференциального уравненияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ОПРЕДЕЛЕНИЕ ОДУ,ЕГО ПОРЯДКА И РЕШЕНИЙ. ОДУ ПЕРВОГО ПОРЯДКА: ОБЩИЕ ОПРЕДЕЛЕНИЯ И ИХ ГЕОМЕТРИЧЕСКАЯ ТРАКТОВКА,ТЕОРЕМА СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ РЕШЕНИЯ ЗАДАЧИ КОШИ. ФИЗИЧЕСКАЯ ЗАДАЧА, ПРИВОДЯЩАЯ К ПОНЯТИЮ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ С некоторой высоты брошено тело массой m. Составить уравнение для скорости падения этого тела в любой момент времени от начала падения, если на него, кроме силы тяжести, действует сила сопротивления воздуха, прямо пропорциональная скорости падения. РЕШЕНИЕ. В момент времени Так как все векторы, обозначенные в задаче, являются коллинеарными, то уравнение падения тела можно записать в скалярной форме:
Такое уравнение называется дифференциальным, так как в него входит производная искомой функции V(t). Решить это дифференциальное уравнение (далее ДУ) – это значит найти функцию V(t), удовлетворяющую ДУ при любом t. Для однозначного определения этой функции нужны еще так называемые начальные условия – это начальная скорость, с которой тело брошено с фиксированной высоты: ОБЩИЕ ПОНЯТИЯ, СВЯЗАННЫЕ С ДИФФЕРЕНЦИАЛЬНЫМИ УРАВНЕНИЯМИ
ПРИМЕРЫ 1) 2) 3) 4) ЗАМЕЧАНИЯ. 1. Чтобы уравнение было дифференциальным, в него могут явно не входить 2. Обыкновенные дифференциальные уравнения содержат неизвестную функцию, зависящую от одной переменной. Такие и будем рассматривать. Если неизвестная функция зависит от нескольких переменных, то ДУ называют дифференциальным уравнением в частных производных.
ПРИМЕР 1. Рассмотрим Его общим решением является функция Частными решениями рассматриваемого ДУ являются функции: Особым решением является функция НАЧАЛЬНЫЕ УСЛОВИЯ. Для выделения частного решения из общего решения ставят так называемые начальные условия к дифференциальному уравнению. Для ДУ n -ого порядка эти условия имеют следующий вид:
где Таким образом: количество начальных условий совпадает с порядком ДУ, следовательно, совпадает с количеством произвольных постоянных в общем решении ДУ; суть начальных условий для ДУ n -ого порядка состоит в том, что они задают при фиксированном значении независимой переменной Подставляя начальные условия (2) в общее решение ДУ (1), определяют значения произвольных постоянных ПРИМЕР 2. Для ДУ предыдущего примера РЕШЕНИЕ. Общее решение данного уравнения известно: Подставляя сюда значения Возвращая теперь значение Ответ: РЕШЕНИЕ Разделяем переменные в данном ДУ, пользуясь свойством пропорции: Интегрируем обе части ДУ с разделёнными переменными, добавляя постоянную В результате интегрирования получили общий интеграл исходного ДУ. Переход к общему решению возможен, если сможем выразить Ответ:
ДОКАЗАТЕЛЬСТВО. Пусть (используем свойство линейности операции дифференцирования) ЗАМЕЧАНИЯ. 1. В общем случае линейного неоднородного уравнения с постоянными коэффициентами и правой части специального общего вида (2) частное решение ищется в следующем виде: Здесь r – это кратность чисел (α±iβ) как корней характеристического уравнения (r = 0 – не являются корнями, r=1 – простые корни, r=2 – двукратные корни и т.д.). 2. Принцип суперпозиции (наложения) частных решений ЛНДУ позволяет расширить возможности работы по сформулированным правилам 1 и 2. ПРИМЕР 4. Найти общее решение ЛНДУ РЕШЕНИЕ. Находим где По принципу наложения частных решений составляем Находим по правилу 2 составляем и находим коэффициенты А и В: таким образом, проверка ДУ: Находим по правилу 1 составляем ДУ: Ответ: ОБОСНОВАНИЕ МЕТОДА ВАРИАЦИИ Функцию (4) так как для определения одной функции
тогда первая производная ДУ (1):
(здесь учтено, что Таким образом, взяв – это система линейных алгебраических уравнений относительно c1' и c2'; главный определитель системы по теореме Крамера, система (5) имеет единственное решение. Решив систему (5), получим производные неизвестных функций c1' и c2' одной переменной; сами функции можно восстановить по их производным с помощью неопределенного интеграла, то есть Обоснование метода вариации закончено. ПРИМЕР 1. Найти общее решение ДУ РЕШЕНИЕ. Данное диф. уравнение имеет тип ЛНДУ с постоянными коэффициентами, поэтому его общее решение составляем по формуле Находим функции с1(х) и с2(х) определяются функциональной системой уравнений (5), которая в данной задаче имеет следующий вид: Подставим Так как ЗАМЕЧАНИЯ. 1.Нормальная система ДУ вида (1) относительно n произвольных функций сводится методом исключения к одному ДУ n -го порядка, поэтому в общее решение системы должно войти ровно n произвольных постоянных, и для их нахождения нужно ставить n начальных условий 2. Если в систему ДУ входят производные высших порядков, то ее всегда можно привести к нормальной форме введением вспомогательных функций, а только после этого просчитать порядок того ДУ, к которому сведется система методом исключения, а следовательно, и количество произвольных постоянных. Пример 2.Рассмотрим механическое движение материальной точки ускорение равнодействующая сила Запишем уравнение движения в скалярной форме и получим систему дифференциальных уравнений относительно функций Сводим систему к нормальной форме с помощью вспомогательных функций Система в нормальной форме: Эта система сведется к ДУ VI порядка и в ее общее решение будет входить 6 произвольных констант (точнее, не более 6, так как иногда система n уравнений сводится к одному ДУ более низкого порядка, чем n; это бывает в случае, когда среди уравнений системы нет независимости и часть из них является следствием других уравнений). 3. При решении нормальных систем ДУ методом повышения порядка сохраняется тип ДУ исходной системы, в частности, гарантированно сохраняется линейность, то есть если все ДУ системы являются линейными, то и сведение будет к линейному ДУ. Также сохраняется постоянство коэффициентов и однородность или неоднородность ДУ. Это дает возможность отдельно построить теорию решения линейных систем с постоянными коэффициентами. Так можно рассмотреть нормальную систему линейных однородных ДУ с постоянными коэффициентами:
(в скобках написано выражение для случая неоднородных ДУ) неизвестные функции: Решение такой однородной системы (4) естественно искать в виде набора экспонент Здесь Подставив эти функции в систему (4), получим: Это система линейных алгебраических уравнений относительно Набор Для существования нетривиальных решений однородной системы необходимо и достаточно, чтобы главный определитель системы был равен 0, то есть Это равенство называется характеристическим уравнением для системы ДУ (4), оно является алгебраическим уравнением n -ной степени относительно числа k и, следовательно, имеет ровно n корней на множестве комплексных чисел С. Далее по корням характеристического уравнения разрабатывается теория записи общего решения системы, аналогичная правилу составления ФСЧР и общего решения линейного однородного ДУ с постоянными коэффициентами n -го порядка. 4. Система линейных ДУ с постоянными коэффициентами часто записывается и решается в матричном виде: (4) Характеристическое уравнение этой системы имеет вид 5. Понятие фазового пространства. Рассмотрим систему трех ДУ относительно трех функций Решение этой системы всегда можно трактовать как траекторию движения точки с координатами Аналогично решение системы относительно n неизвестных функций можно трактовать как уравнение линии (траектории движения) точки в пространстве R n, которое и называется фазовым пространством для данной системы ДУ. Такая трактовка дает возможность проиллюстрировать решения системы ДУ в виде некоторых линий в фазовом пространстве. ОПРЕДЕЛЕНИЕ ОДУ,ЕГО ПОРЯДКА И РЕШЕНИЙ. ОДУ ПЕРВОГО ПОРЯДКА: ОБЩИЕ ОПРЕДЕЛЕНИЯ И ИХ ГЕОМЕТРИЧЕСКАЯ ТРАКТОВКА,ТЕОРЕМА СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ РЕШЕНИЯ ЗАДАЧИ КОШИ. ФИЗИЧЕСКАЯ ЗАДАЧА, ПРИВОДЯЩАЯ К ПОНЯТИЮ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ С некоторой высоты брошено тело массой m. Составить уравнение для скорости падения этого тела в любой момент времени от начала падения, если на него, кроме силы тяжести, действует сила сопротивления воздуха, прямо пропорциональная скорости падения. РЕШЕНИЕ. В момент времени Так как все векторы, обозначенные в задаче, являются коллинеарными, то уравнение падения тела можно записать в скалярной форме:
Такое уравнение называется дифференциальным, так как в него входит производная искомой функции V(t). Решить это дифференциальное уравнение (далее ДУ) – это значит найти функцию V(t), удовлетворяющую ДУ при любом t. Для однозначного определения этой функции нужны еще так называемые начальные условия – это начальная скорость, с которой тело брошено с фиксированной высоты:
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 995; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.182.15 (0.013 с.) |

 составляем уравнение падения тела, используя II закон Ньютона:
составляем уравнение падения тела, используя II закон Ньютона: , где
, где 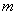 - масса тела,
- масса тела,  - ускорение тела,
- ускорение тела,  - скорость тела,
- скорость тела, - равнодействующая всех сил, приложенных к телу в его центре масс.
- равнодействующая всех сил, приложенных к телу в его центре масс.
 – это есть уравнение относительно искомой скорости V(t), так как оно выполняется в любой момент времени t.
– это есть уравнение относительно искомой скорости V(t), так как оно выполняется в любой момент времени t. , где
, где 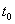 – момент времени, когда тело брошено,
– момент времени, когда тело брошено, 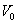 – число, равное модулю начальной скорости падения. Если же начальные условия не ставить, то дифференциальному уравнению (*) будет удовлетворять бесконечно много функций
– число, равное модулю начальной скорости падения. Если же начальные условия не ставить, то дифференциальному уравнению (*) будет удовлетворять бесконечно много функций 
 , неизвестной функцией
, неизвестной функцией  и ее производными по
и ее производными по 
 - ДУ II порядка относительно функции
- ДУ II порядка относительно функции  ;
; - ДУ III порядка относительно функции
- ДУ III порядка относительно функции 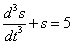 - ДУ III порядка относительно функции
- ДУ III порядка относительно функции  ;
; .
.
 ,
зависящая от аргумента
,
зависящая от аргумента  произвольных постоянных
произвольных постоянных 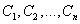 и удовлетворяющая ДУ при любых значениях этих постоянных.
Частным решениемДУ называется его решение, получающееся из общего решения этого ДУ при фиксированных значениях постоянных
и удовлетворяющая ДУ при любых значениях этих постоянных.
Частным решениемДУ называется его решение, получающееся из общего решения этого ДУ при фиксированных значениях постоянных 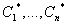 :
: 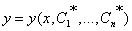 .
Особым решением ДУ называется такое его решение, которое не может быть получено из его общего решения ни при каких фиксированных значениях произвольных постоянных
.
Особым решением ДУ называется такое его решение, которое не может быть получено из его общего решения ни при каких фиксированных значениях произвольных постоянных 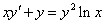 - ДУ I порядка относительно функции
- ДУ I порядка относительно функции  ,так как при подстановке этой функции в ДУ получаем тождественно по
,так как при подстановке этой функции в ДУ получаем тождественно по  :
: 

 - верно при любых
- верно при любых 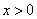 и любых значениях
и любых значениях 
 , так как она удовлетворяет ДУ, но не получается из общего решения ни при каком значении
, так как она удовлетворяет ДУ, но не получается из общего решения ни при каком значении  ,
,
 - это фиксированные числа.
- это фиксированные числа. значения неизвестной функции
значения неизвестной функции  и всех её производных до (n- 1 ) -ого порядка включительно.
и всех её производных до (n- 1 ) -ого порядка включительно.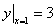 .
. и
и 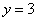 из начальных условий, получим равенство для определения значения
из начальных условий, получим равенство для определения значения  .
.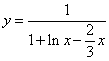 - это и есть решение поставленной задачи Коши.
- это и есть решение поставленной задачи Коши. .
. – получили ДУ с разделёнными переменными.
– получили ДУ с разделёнными переменными.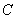 :
:
 .
. через
через 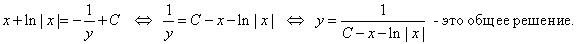

 – частные решения ДУ (3). Подставив их в ДУ получим тождества по x:
– частные решения ДУ (3). Подставив их в ДУ получим тождества по x:


 функция
функция  тождественно удовлетворяет исходному ДУ (3), следовательно, является его решением, ч.т.д.
тождественно удовлетворяет исходному ДУ (3), следовательно, является его решением, ч.т.д. .
. – большая из степеней многочленов
– большая из степеней многочленов 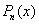 и
и  ;
; -- целые многочлены степени k, взятые в самом общем виде с неопределенными коэффициентами;
-- целые многочлены степени k, взятые в самом общем виде с неопределенными коэффициентами;
 Находим
Находим  .
. :
:  ,
, – подходит под второй специальный вид,
– подходит под второй специальный вид, – подходит под первый специальный вид.
– подходит под первый специальный вид. , где
, где  удовлетворяет ДУ
удовлетворяет ДУ  ,
,  удовлетворяет ДУ
удовлетворяет ДУ  .
. - второй специальный вид, в котором
- второй специальный вид, в котором 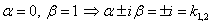 ;
;
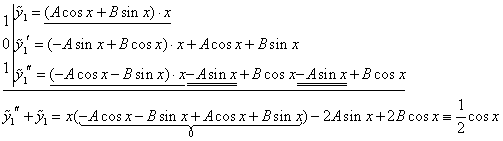

 ;
;
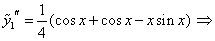
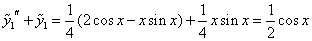 – верно.
– верно.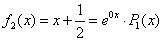 – первый специальный вид, в котором
– первый специальный вид, в котором  ;
; и находим коэффициенты
и находим коэффициенты  :
: ;
; .
. .
. будем дифференцировать и подставлять в ДУ (1):
будем дифференцировать и подставлять в ДУ (1): ;
; и
и  , то тем самым в задаче получился произвол, которым можно распорядиться удобным образом, например, в
, то тем самым в задаче получился произвол, которым можно распорядиться удобным образом, например, в  ;
;
 упрощается, и находим вторую производную:
упрощается, и находим вторую производную:




 и
и  – это частные решения ЛОДУ (2)).
– это частные решения ЛОДУ (2)).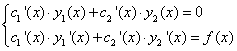
 , так как
, так как  ;
; .
. .
. , причем,
, причем, 
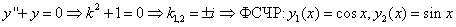
 . Находим
. Находим 
 - не подходит ни под первый, ни под второй специальный вид, поэтому
- не подходит ни под первый, ни под второй специальный вид, поэтому  заменяем на функции от x:
заменяем на функции от x:  ;
; Решаем систему по формулам Крамера:
Решаем систему по формулам Крамера: ;
;  ;
; 

 ,
,  .
. в функцию
в функцию  .
.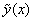 -- это какое-нибудь частное решение данного неоднородного ДУ, то входящими в него константами интегрирования
-- это какое-нибудь частное решение данного неоднородного ДУ, то входящими в него константами интегрирования  можно распорядиться любым удобным образом, например, положить
можно распорядиться любым удобным образом, например, положить  . Найденное
. Найденное 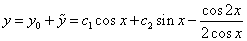 – это общее решение данного ДУ.
– это общее решение данного ДУ. , начальные условия
, начальные условия 
 ,
, ,
,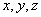 – координаты движущейся точки (функции от t, t-время),
– координаты движущейся точки (функции от t, t-время), .
. ,
, 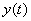 ,
,  :
:
 :
: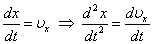 ,
, 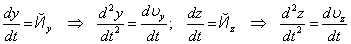 .
.

 ;
;  - числа или const по t, называются коэффициентами системы линейных ДУ.
- числа или const по t, называются коэффициентами системы линейных ДУ.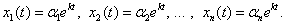
 - это числа, которые подбираются из условия, что все функции x1(t), x2(t), …, xn(t) удовлетворяют исходной системе ЛОДУ.
- это числа, которые подбираются из условия, что все функции x1(t), x2(t), …, xn(t) удовлетворяют исходной системе ЛОДУ.
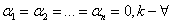 является тривиальным решением этой системы, но он приводит и к тривиальному решению системы ДУ
является тривиальным решением этой системы, но он приводит и к тривиальному решению системы ДУ  . Для нахождения нетривиальных решений запишем систему как однородную относительно
. Для нахождения нетривиальных решений запишем систему как однородную относительно  :
: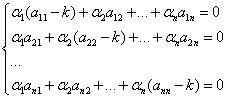
 .
. , где
, где 
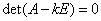 , где
, где  - это единичная матрица порядка n. Работа с системой (4) становится более компактной.
- это единичная матрица порядка n. Работа с системой (4) становится более компактной. , записанную в нормальной форме:
, записанную в нормальной форме: 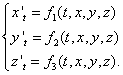
 является параметрическими уравнениями этой траектории движения.
является параметрическими уравнениями этой траектории движения.


