
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приводящие к дифференциальным уравнениямСодержание книги
Поиск на нашем сайте
К дифференциальным уравнениям приводят многие задачи механики, физики, астрономии и других естественных наук, а также многие проблемы техники. Поясним на примерах, как возникают в исследованиях дифференциальные уравнения.
Решение. Пусть M (x, y) точка касания. Так как
Положим X = 0, тогда
Соотношение является примером дифференциального уравнения. Оно содержит наряду с неизвестной функцией y и ее производную Функцию y = y (x) ¹ 0 из уравнения легко найти:
где С – произвольная константа (постоянная интегрирования), удобно ее взять в виде ln C. Тогда
Заметим, что уравнению удовлетворяет целое семейство кривых, зависящих от параметра С. Чтобы выделить какую-то одну кривую из семейства, надо указать константу С. Для этого достаточно задать на плоскости XOY точку (x 0, y 0), через которую эта кривая проходит. Тогда постоянную С, соответствующую этой кривой, найдем, положив в равенстве y = y 0 при x = x 0. Пусть y = 2 при x = 1, тогда
Таким образом, искомая кривая семейства, проходящая через точку (1, 2), определяется равенством
Задача 9.1.2. Тело брошено вертикально вверх с начальной скоростью v 0. Определить закон движения, предполагая, что тело движется только под влиянием силы тяжести. Решение. Под влиянием силы тяжести тело движется с постоянным ускорением g. Ввиду того, что ускорение выражается производной второго порядка от пути по времени, из
Получили дифференциальное уравнение, содержащее производную 2-го порядка. Интегрируя дважды, получим
Постоянные С 1 и С 2 определим из начальных условий. Так как отсчет пути ведется от начального момента, то при t = 0 S = 0 и, следовательно, С 2 = 0. Так как при t = 0 начальная скорость Итак, зависимость пройденного телом пути S от времени t:
Задача 9.1.3.Скорость обесценивания оборудования вследствие его износа пропорциональна в каждый момент времени его фактической стоимости. Начальная стоимость равна А 0. Найти стоимость оборудования по истечении Т лет. Решение. Пусть A = A (t) - стоимость оборудования в любой момент времени t. Тогда
где k – коэффициент пропорциональности, взятый со знаком минус, так как стоимость убывает. Из следует
Начальное условие: при t = 0 А = А 0, поэтому
Чтобы найти стоимость оборудования по истечении Т лет, подставляем в t = Т.
Как показано в рассмотренных примерах, если мы сумеем проинтегрировать полученное дифференциальное уравнение, то тем самым дадим ответы на вопросы задачи, которая привела нас к нему. Поэтому основной задачей теории интегрирования дифференциальных уравнений является нахождение всех решений данного дифференциального уравнения и изучение свойств этих решений. Заметим, что задачу интегрирования дифференциального уравнения можно понимать по-разному. В самой узкой постановке задачи ставится целью выражение искомых функций через элементарные функции. Эта задача, вообще говоря, не разрешима даже для самого простого уравнения
Несколько шире постановка задачи, при которой уравнение считается разрешенным, если оно приведено к квадратурам (т.е., к операциям взятия неопределенных интегралов). В этом смысле уравнение, очевидно, разрешимо. Все решения этого уравнения содержатся в формуле
Однако следует отметить, что уравнения, интегрируемые в квадратурах, составляют лишь незначительную часть всех дифференциальных уравнений. Так, например, очень важное во многих приложениях уравнение Бесселя
в общем случае не интегрируется в квадратурах. Задача общей теории дифференциальных уравнений состоит в изучении свойств функций, определяемых дифференциальными уравнениями, непосредственно по виду любого заданного дифференциального уравнения, независимо от интегрируемости последнего в элементарных функциях или в квадратурах.
Основные понятия теории дифференциальных уравнений
Определение 9.2.1. Дифференциальным уравнением называется уравнение, связывающее независимую переменную х, неизвестную функцию y = y (x) и ее производные Символически дифференциальное уравнение можно записать так:
Если уравнение можно записать в виде
то будем говорить, что дифференциальное уравнение разрешено относительно старшей производной. Оно называется дифференциальным уравнением в нормальной форме. Дифференциальное уравнение, в котором неизвестная функция y зависит от одной переменной x, называется обыкновенным. Если же дифференциальное уравнение содержит неизвестную функцию нескольких переменных и ее частные производные, то оно называется уравнением в частных производных. В данном модуле мы будем изучать только обыкновенные дифференциальные уравнения и слово «обыкновенные» будем в дальнейшем опускать.
Определение 9.2.2. Порядком дифференциального уравнения называется наивысший порядок производной искомой функции, входящей в уравнение. Так, соотношения и – дифференциальные уравнения первого порядка, уравнение – второго порядка, а уравнение
Определение 9.2.3. Решением (или интегралом)дифференциального уравнения называется всякая функция y = f (x), которая, будучи подставлена в уравнение, превращает его в тождество.
Пример 9.2.1.Пусть дано уравнение Функция y = sin x, y = 2cos x, y = 3sin x - cos x и вообще функции вида y = C 1sin x, y = C 2cos x или y = C 1sin x + C 2cos x являются решениями данного уравнения при любом выборе постоянных С 1 и С 2; в этом легко убедиться, подставив указанные функции и их вторые производные в уравнение. Всякому решению дифференциального уравнения или на плоскости отвечает некоторая кривая y = y (x), x Î (a, b), которая называется интегральной кривой (линией) дифференциального уравнения. Процесс нахождения решения дифференциального уравнения называется интегрированием этого уравнения. Дифференциальное уравнение, как правило, имеет бесчисленное множество решений (задачи 9.1.1 – 9.1.3 и пример 9.2.1 подтверждают это). Чтобы выделить какое-то одно решение дифференциального уравнения, необходимо задание некоторых дополнительных условий. Таким условием для уравнения является задание точки (x 0, y 0) плоскости XOY, через которую должна проходить интегральная кривая этого уравнения. В задаче 9.1.2 для дифференциального уравнения этими условиями явились начальный путь S = 0 при t = 0 и начальная скорость v = v 0 при t = 0. В задаче 9.1.3 – начальная стоимость оборудования А = А 0 при t = 0.
|
||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 1288; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.72.27 (0.007 с.) |

 Задача 9.1.1.Найти уравнение кривой линии, у которой отрезок касательной, заключенный между осями координат, делится пополам в точке касания.
Задача 9.1.1.Найти уравнение кривой линии, у которой отрезок касательной, заключенный между осями координат, делится пополам в точке касания. равен тангенсу угла наклона к оси OX касательной, проведенной в точке
равен тангенсу угла наклона к оси OX касательной, проведенной в точке  кривой, то уравнение касательной будет следующим
кривой, то уравнение касательной будет следующим .
. и точка В имеет координаты
и точка В имеет координаты  . По условию точка касания делит отрезок АВ пополам, поэтому
. По условию точка касания делит отрезок АВ пополам, поэтому  ,
,  . Последнее равенство принимает вид:
. Последнее равенство принимает вид: .
.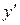 .
. ,
, .
. .
. .
.
 .
. ,
, .
. , то из уравнения получаем C 1 = v 0.
, то из уравнения получаем C 1 = v 0. .
. - скорость обесценивания оборудования вследствие его износа. Из условия задачи следует, что
- скорость обесценивания оборудования вследствие его износа. Из условия задачи следует, что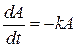 ,
, Þ
Þ  Þ
Þ 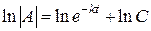 . Потенцируя, получаем:
. Потенцируя, получаем: .
. , C = A 0. Подставляя C = A 0 в, получаем
, C = A 0. Подставляя C = A 0 в, получаем .
. .
. , ибо, как известно, не всегда первообразная для элементарной функции представляет собой тоже элементарную функцию. В качестве примера можно взять уравнение
, ибо, как известно, не всегда первообразная для элементарной функции представляет собой тоже элементарную функцию. В качестве примера можно взять уравнение .
. .
.

 (наличие хотя бы одной производной обязательно).
(наличие хотя бы одной производной обязательно).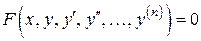 .
. ,
, является дифференциальным уравнением четвертого порядка.
является дифференциальным уравнением четвертого порядка. .
.


