
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод подстановки (Бернулли)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
По этому методу искомое решение уравнения будем искать в виде
где
Выберем функцию
после чего от уравнения остается
В результате получили систему двух уравнений
Сначала решаем первое уравнение системы, которое является линейным однородным дифференциальным уравнением относительно v и
Подставляя функцию v во второе уравнение системы, получаем еще одно уравнение с разделяющимися переменными
Таким образом,
Так как С 1 и С 2 – произвольные постоянные, то С 1 С 2 - тоже произвольная постоянная, которую можно обозначить через С. В итоге получаем, что общим решением неоднородного дифференциального уравнения будет
Поскольку при перемножении функций
Пример 9.6.1. Решить уравнение Решение. Пусть y = uv,
Составим систему
Решаем первое уравнение Подставляем В итоге находим, что общее решение данного уравнения
Метод вариации произвольного постоянного (метод Лагранжа) Найдем общее решение однородного дифференциального уравнения. Разделив в нем переменные, получим
где С – произвольная постоянная. По методу вариации (в переводе на русский язык, изменения) произвольной постоянной общее решение неоднородного уравнения ищется в виде
в котором Найдем
откуда
Итак, функция
совпадающее с решением.
Пример 9.6.2. Найти частное решение дифференциального уравнения Решение. В начале решаем соответствующее однородное уравнение В соответствии с методом Лагранжа общее решение ищем в виде Итак, искомым частным решением данного уравнения, удовлетворяющим начальному условию
Общее решение уравнения можно сразу найти по формуле, подставив туда Замечание. В приложениях часто встречаются линейные уравнения с постоянными коэффициентами
где a и b – постоянные. Его можно решить путем разделения переменных:
Уравнение Бернулли Рассмотрим уравнение вида
где Разделив обе части уравнения на
Сделаем, далее, замену Умножим обе части уравнения на
т.е. получили линейное дифференциальное уравнение относительно z и
Пример 9.7.1. Найти общее решение дифференциального уравнения Решение. Предполагая х ¹ 0, разделим обе части дифференциального уравнения на х, тогда Сделаем подстановку
Так как Замечание. Дифференциальное уравнение можно сразу решать методом Бернулли или Лагранжа, не сводя его к линейному.
Пример 9.7.2. Решить уравнение Решение. Это уравнение Бернулли. Решение будет искать в виде
Выберем функцию v (x) таким образом, чтобы Решим первое уравнение системы
|
|||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 588; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.7.53 (0.011 с.) |

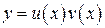 ,
,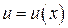 и
и  - некоторые непрерывно дифференцируемые функции. Подставляя y = uv и
- некоторые непрерывно дифференцируемые функции. Подставляя y = uv и  в, получаем
в, получаем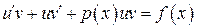 или
или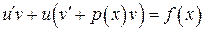 .
.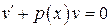 ,
,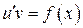 .
.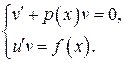
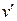 . Покажем, что оно, в то же время, и уравнение с разделяющимися переменными.
. Покажем, что оно, в то же время, и уравнение с разделяющимися переменными.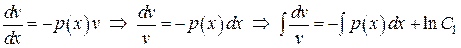 Þ
Þ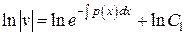 Þ
Þ 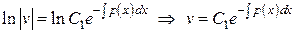 .
.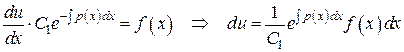 , откуда
, откуда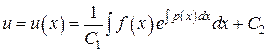 .
.
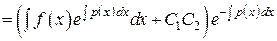 .
.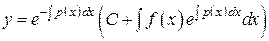 .
.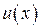 и
и 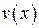 постоянная С 1 во втором слагаемом сократилась, то в качестве функции
постоянная С 1 во втором слагаемом сократилась, то в качестве функции  .
.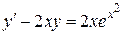 .
.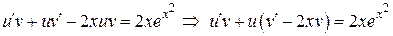 .
.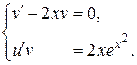
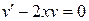 Þ
Þ 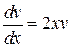 Þ
Þ 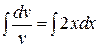 Þ
Þ 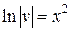 Þ
Þ 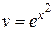 (постоянную здесь не берем).
(постоянную здесь не берем).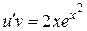 Þ
Þ 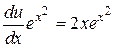 Þ
Þ 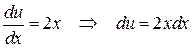 Þ
Þ 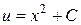 .
.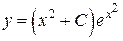 .
.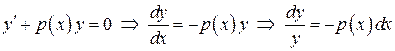 Þ
Þ Þ
Þ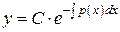 ,
, ,
,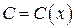 – неизвестная дифференцируемая функция.
– неизвестная дифференцируемая функция.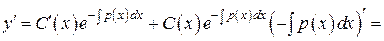
 . Подставляя y и
. Подставляя y и 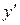 в, получаем
в, получаем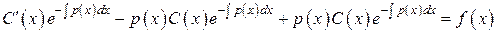 ,
,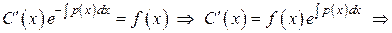
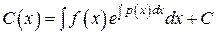 .
.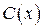 найдена. Подставляя ее в, находим общее решение уравнения
найдена. Подставляя ее в, находим общее решение уравнения ,
,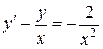 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 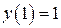 .
.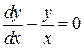 Þ
Þ 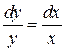 Þ
Þ 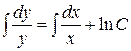 Þ
Þ  Þ
Þ 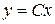 .
.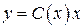 . Находим
. Находим 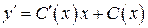 . Тогда
. Тогда 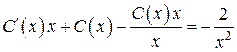 Þ
Þ 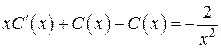 Þ
Þ 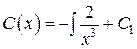 Þ
Þ 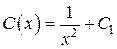 и
и 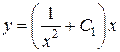 , или
, или  будет общим решением данного уравнения. Из условия
будет общим решением данного уравнения. Из условия 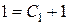 Þ
Þ  .
. .
.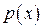 и
и 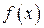 и взяв три интеграла.
и взяв три интеграла.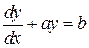 ,
,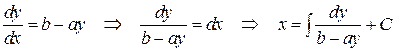 .
.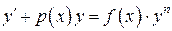 ,
, , получим
, получим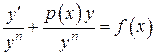 , или
, или 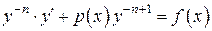 .
.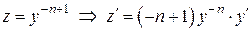 .
.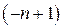 .
.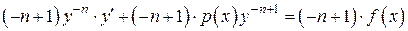 Þ
Þ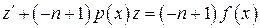 ,
,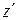 . Найдя его общий интеграл и подставив
. Найдя его общий интеграл и подставив 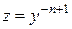 , получим общий интеграл уравнения Бернулли.
, получим общий интеграл уравнения Бернулли.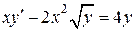 .
.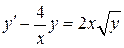 является уравнением Бернулли, где
является уравнением Бернулли, где 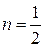 . Умножим обе части уравнения на
. Умножим обе части уравнения на  , в результате имеем
, в результате имеем 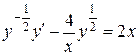 .
.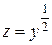 Þ
Þ 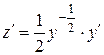 . Умножая обе части последнего дифференциального уравнения на
. Умножая обе части последнего дифференциального уравнения на  , получим
, получим 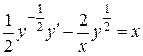 ,
, 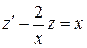 , а это уже линейное дифференциальное уравнение относительно z и
, а это уже линейное дифференциальное уравнение относительно z и 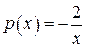 , f (x) = x.
, f (x) = x.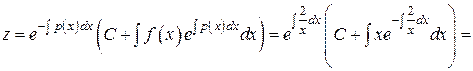
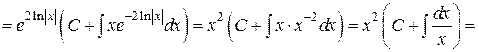
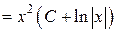 .
.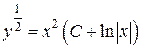 Þ
Þ 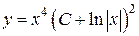 – искомое общее решение.
– искомое общее решение.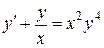 .
. Þ
Þ 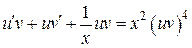 Þ
Þ 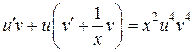 .
.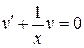 . В результате получаем систему:
. В результате получаем систему: 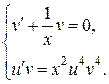
 Þ
Þ  Þ
Þ  Þ
Þ 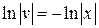 Þ
Þ 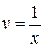 . Тогда второе уравнение системы
. Тогда второе уравнение системы 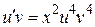 принимает вид
принимает вид  Þ
Þ  Þ
Þ 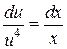 Þ
Þ  Þ
Þ 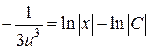 Þ
Þ 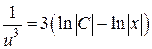 Þ
Þ 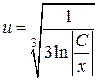 . Итак,
. Итак, 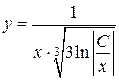 будет общим решением исходного уравнения.
будет общим решением исходного уравнения.


