
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные неоднородные дифференциальные уравнения.Содержание книги
Поиск на нашем сайте
Метод вариации произвольных постоянных Рассмотрим сначала линейное неоднородное уравнение второго порядка
где а 1, а 2, f (x) – либо непрерывные функции, либо постоянные числа. Структура общего решения такого уравнения определяется следующей теоремой.
Теорема 9.17.1.Общее решение неоднородного уравнения представляет собой сумму какого-нибудь частного решения этого уравнения уч и общего решения уодн соответствующего однородного уравнения
Из теоремы следует, что у=уодн + уч. Таким образом, если известно общее решение соответствующего однородного уравнения, то основная задача решения неоднородного уравнения состоит в нахождении какого-либо его частного решения. Укажем общий метод нахождения частного решения неоднородного уравнения.
Метод вариации произвольных постоянных (Лагранжа) Предположим известно общее решение однородного уравнения
где у 1 и у 2 – линейно независимые частные решения однородного уравнения. Будем искать частное решение неоднородного уравнения в виде
рассматривая С 1 и С 2 как некоторые пока неизвестные функции. Продифференцируем равенство:
Подберем искомые функции
Тогда Подставляя
или
Выражения, стоящие в первых двух скобках, обращаются в нуль, так как у 1 и у 2 – решения однородного уравнения. Следовательно, последнее равенство имеет вид
Объединяя уравнения и, получаем для определения производных от неизвестных функций
Определитель этой системы Подставляя полученные функции
Пример 9.17.1.Найти общее решение уравнения Решение. Найдем общее решение однородного уравнения
Частное решение неоднородного уравнения ищем в виде
( Составляем систему
Тогда
При отыскании частных решений иногда полезно использовать следующую теорему.
Теорема 9.17.2.Частное решение уравнения
где правая часть есть сумма двух функций
Упражнение.Доказать теорему самостоятельно. Для уравнения третьего порядка
а система выглядит следующим образом
Аналогично можно найти частное решение и для уравнений более высокого порядка.
Линейные неоднородные дифференциальные уравнения
|
|||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 308; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.67.169 (0.007 с.) |

 ,
, .
. ,
, ,
,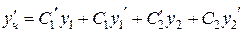 .
. и
и 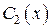 так, чтобы
так, чтобы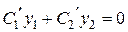 .
. Þ
Þ  .
. ,
,  ,
,  в, получим
в, получим
 .
. .
.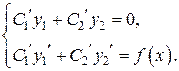
 , так как у 1 и у 2 – линейно независимые решения. Поэтому система имеет единственное решение. Решая ее, найдем
, так как у 1 и у 2 – линейно независимые решения. Поэтому система имеет единственное решение. Решая ее, найдем  (так как мы ищем частное решение, то постоянные интегрирования не берем).
(так как мы ищем частное решение, то постоянные интегрирования не берем). .
. Þ
Þ 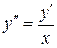 Þ
Þ  Þ
Þ  Þ
Þ  Þ
Þ 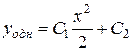 .
.
 ,
,  – частные решения однородного уравнения).
– частные решения однородного уравнения).
 , а общее решение
, а общее решение .
.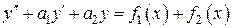 ,
,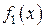 и
и  , можно представить в виде суммы
, можно представить в виде суммы 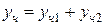 , где
, где  и
и  – частные решения, соответственно, уравнений
– частные решения, соответственно, уравнений ,
, .
. ,
, ,
,



