
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условия линейной зависимости и независимости решенийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Установим некоторые основные свойства линейных однородных уравнений на примере уравнений второго порядка.
Теорема 9.15.1.Если у 1 и у 2 - два частных решения линейного однородного уравнения второго порядка
то у 1 + у 2 будет решением этого уравнения. Доказательство. Так как у 1 и у 2 – решения, то
Подставим у 1 + у 2 в левую часть:
Теорема 9.15.2.Если у 1 - решение уравнения и С - постоянная, то Су 1 будет тоже решением этого уравнения. Доказательство.
Определение 9.15.1.Два решения уравнения у 1 и у 2 будем называть линейно независимыми на отрезке Иными словами, два решения у 1 и у 2 называются линейными зависимыми на
Пример 9.15.1.Пусть дано уравнение
Определение 9.15.2.Если у 1 и у 2 - функции от х, то определитель
называется определителем Вронского, или вронскианом данных функций. Для трех функций
Теорема 9.15.3. Если функции у 1 и у 2 линейно зависимы на отрезке Доказательство. Действительно, если
Теорема 9.15.4. Если решения у 1 и у 2 уравнения линейно независимы на отрезке Заметим, что теорема верна для дифференциального уравнения любого порядка до n включительно. Доказательство теоремы не приводим.
Теорема 9.15.5 (о структуре общего решения однородного уравнения). Если у 1 и у 2 – два линейно независимых решения уравнения, то
где С 1 и С 2 – произвольные постоянные, есть его общее решение. Доказательство. Из теорем 9.15.1 и 9.15.2 следует, что функция Докажем далее, что каковы бы ни были начальные условия
Подставляя начальные условия в
Из системы можно найти Для уравнения общее решение имеет вид
где у 1, у 2, …, yn – линейно независимые на Не существует общих методов для нахождения в конечном виде общего решения линейного уравнения (однородного и неоднородного) с переменными коэффициентами. Для уравнений с постоянными коэффициентами такие методы существуют. Мы их сейчас и рассмотрим.
|
|||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 565; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.45.22 (0.009 с.) |

 ,
,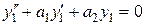 ,
,  .
.
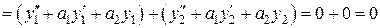 , т.е. у 1 + у 2 тоже решение уравнения.
, т.е. у 1 + у 2 тоже решение уравнения.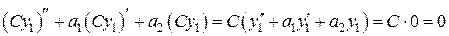 .
. , если их отношение на этом отрезке не является постоянным, т.е. если
, если их отношение на этом отрезке не является постоянным, т.е. если  . В противном случае решения называются линейно зависимыми.
. В противном случае решения называются линейно зависимыми. , что
, что  при
при 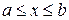 . В этом случае
. В этом случае 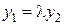 .
. . Легко проверить, что функции
. Легко проверить, что функции  ,
, 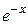 , 3
, 3  при изменении х. Функции же
при изменении х. Функции же 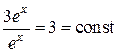 .
.
 и т.д.
и т.д. , где
, где  , то
, то  и
и .
. не обращается в нуль ни в одной точке указанного отрезка.
не обращается в нуль ни в одной точке указанного отрезка. ,
, ,
,  , можно так подобрать значения произвольных постоянных С 1 и С 2, чтобы соответствующее частное решение
, можно так подобрать значения произвольных постоянных С 1 и С 2, чтобы соответствующее частное решение  удовлетворяло эти начальным условиям.
удовлетворяло эти начальным условиям. , будем иметь:
, будем иметь: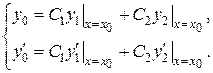
 и
и  единственным образом, так как определитель этой системы
единственным образом, так как определитель этой системы 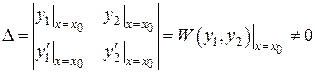 в силу линейной независимости у 1 и у 2. Частное решение
в силу линейной независимости у 1 и у 2. Частное решение  будет удовлетворять начальным условиям. Теорема доказана.
будет удовлетворять начальным условиям. Теорема доказана. ,
,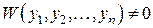 .
.


