Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы решения задач линейного программирования на эвмСодержание книги
Поиск на нашем сайте
Цель: научиться методам решения задач линейного программирования на ЭВМ, рассмотреть основные типы задач – определение оптимального ассортимента продукции, задача составления смеси, целочисленные задачи, в том числе задачи с булевыми переменными. Теоретические материалы по данной теме содержатся в [1, тема 2.2]. Для того чтобы решить задачу линейного программирования (ЛП) в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия. Ввести условие задачи: a) создать экранную форму для ввода условия задачи – переменных, целевой функции (ЦФ), ограничений, граничных условий; б) ввести исходные данные в экранную форму – коэффициенты ЦФ, коэффициенты при переменных в ограничениях, правые части ограничений; в) ввести зависимости из математической модели в экранную форму – формулу для расчета ЦФ, формулы для расчета значений левых частей ограничений; г) задать ЦФ (в окне "Поиск решения") – целевую ячейку, направление оптимизации ЦФ; д) ввести ограничения и граничные условия (в окне "Поиск решения") – ячейки со значениями переменных, граничные условия для допустимых значений переменных, соотношения между правыми и левыми частями ограничений. Решить задачу: a) установить параметры решения задачи (в окне "Поиск решения"); б) запустить задачу на решение (в окне "Поиск решения"); в) выбрать формат вывода решения (в окне "Результаты поиска решения").
ПРИМЕР 1.1. Нахождение решения для следующей задачи ЛП:
–6 х 1+2 х 2+4 х 3– х 4 ≥450, (1.1) 4 х 1–1,5 х 2+10,4 х 3+13 х 4≤89, х j≥0, j=1,…,4. F(Х)=130,5 х 1+20 х 2+56 х 3+87,8 х 4→ max; (1.2) Ввод исходных данных Создание экранной формы и ввод в нее условия задачи Экранная форма для ввода условий задачи (1.1)–(1,2) вместе с введенными в нее исходными данными представлена на рис.1.1.
В экранной форме на рис.1.1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Так, например, переменным задачи (1.1) соответствуют ячейки B3(х 1), C3(х 2), D3(х 3), E3(х 4), коэффициентам ЦФ соответствуют ячейки B6(с 1=130,5), C6(с 2=20), D6(с 3=56), E6(c 4=87,8), правым частям ограничений соответствуют ячейки H10(b 1=756), H11(b 2=450), H12(b 3=89) и т.д. Ввод зависимостей из математической модели в экранную форму Зависимость для ЦФ В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Значение ЦФ определяется выражением (1.2) Используя обозначения соответствующих ячеек в Excel (см. рис.1.1), формулу для расчета ЦФ (1.2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3, D3, E3), на соответствующую ячейку, отведенную для коэффициентов ЦФ (B6, C6, D6, E6). Чтобы задать эту формулу необходимо в ячейку F6 ввести следующее выражение и нажать клавишу "Enter" =СУММПРОИЗВ(B$3:E$3;B6:E6), (1.3) где символ $ перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится; символ: означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия (например, запись B6:E6 указывает на ячейки B6, C6, D6 и E6). После этого в целевой ячейке появится 0 (нулевое значение) (рис. 1.2).
Рисунок 1.2. Экранная форма задачи (1.1)–(1,2) после ввода всех необходимых формул (курсор в ячейке F6) Примечание 1. Существует другой способ задания функций в Excel с помощью режима "Вставка функций", который можно вызвать из меню "Вставка" или при нажатии кнопки " fх " на стандартной панели инструментов. Так, например, формулу (1.3) можно задать следующим образом: • курсор в поле F6; • нажав кнопку " fх ", вызовите окно "Мастер функций – шаг 1 из 2"; • выберите в окне "Категория" категорию "Математические"; • в окне "Функция" выберите функцию СУММПРОИЗВ; • в появившемся окне "СУММПРОИЗВ" в строку "Массив 1" введите выражение B$3:E$3, а в строку "Массив 2" – выражение B6:E6 (рис.1.3); • после ввода ячеек в строки "Массив 1" и "Массив 2" в окне "СУММПРОИЗВ" появятся числовые значения введенных массивов (см. рис.1.3), а в экранной форме в ячейке F6 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).
Рисунок 1.3. Ввод формулы для расчета ЦФ в окно "Мастер функций" Зависимости для левых частей ограничений Левые части ограничений задачи (1.1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3, D3, E3), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B10, C10, D10, E10 – 1-е ограничение; B11, C11, D11, E11 – 2-е ограничение и B12, C12, D12, E12 – 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл. 1. Формулы, описывающие ограничения модели (1.1) Таблица 1
Как видно из табл. 1, формулы, задающие левые части ограничений задачи (1.1), отличаются друг от друга и от формулы (1.3) в целевой ячейке F6 только номером строки во втором массиве. Этот номер определяется той строкой, в которой ограничение записано в экранной форме. Поэтому для задания зависимостей для левых частей ограничений достаточно скопировать формулу из целевой ячейки в ячейки левых частей ограничений. Для этого необходимо: • поместить курсор в поле целевой ячейки F6 и скопировать в буфер содержимое ячейки F6 (клавишами "Ctrl-Insert"); • помещать курсор поочередно в поля левой части каждого из ограничений, то есть в F10, F11 и F12, и вставлять в эти поля содержимое буфера (клавишами "Shift-Insert") (при этом номер ячеек во втором массиве формулы будет меняться на номер той строки, в которую была произведена вставка из буфера); • на экране в полях F10, F11 и F12 появится 0 (нулевое значение) (см. рис.1.2). Задание ЦФ Дальнейшие действия производятся в окне "Поиск решения" (Solver Add-in), которое для версии 2003 вызывается из меню "Сервис". Для первоначальной активации опции "Поиск решения" в меню "Сервис" нажмите «Надстройки», в появившемся окне отметьте "Поиск решения" и нажмите «ОК». Далее действуйте по инструкции. Для версии 2007 щелкните значок Кнопка Microsoft Office В случае появления сообщения о том, что пакет Поиск решения не установлен на компьютере и предложения установить его, нажмите кнопку Да. После загрузки в версии 2003 команда Поиск решения становится доступной в пункте Сервис, а в версии 2007 и 2010 на вкладке Данные. После завершения генерации вызывайте " Поиск решения " (рис. 1.4) и: • поставьте курсор в поле " Установить целевую "(Set Target Cell); • введите адрес целевой ячейки $F$6 или сделайте одно нажатие левой клавиши мыши на целевую ячейку в экранной форме – это будет равносильно вводу адреса с клавиатуры; • введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке " Равной: максимальному значению "(Equal to … Max … Value of:).
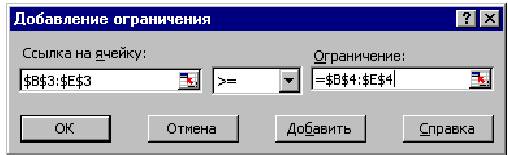
Рисунок 1.4. Окно " Поиск решения " задачи (1.1)–(1,2) Ввод ограничений и граничных условий Задание ячеек переменных В окно " Поиск решения " в поле " Изменяя ячейки " (By Changing Cell) впишите адреса $B$3:$E$3. Необходимые адреса можно вносить в поле " Изменяя ячейки " и автоматически путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме. Задание граничных условий для допустимых значений переменных В нашем случае на значения переменных накладывается только граничное условие неотрицательности, то есть их нижняя граница должна быть равна нулю (см. рис. 1.1). • Нажмите кнопку " Добавить "(Add), после чего появится окно " Добавление ограничения " (Add Constraints) (рис. 1.5). • В поле " Ссылка на ячейку "(Cell Reference) введите адреса ячеек переменных $B$3:$E$3. Это можно сделать как с клавиатуры, так и путем выделения мышью всех ячеек переменных непосредственно в экранной форме. • В поле знака откройте список предлагаемых знаков и выберите ≥. • В поле " Ограничение " (Subject to the Constraints) введите адреса ячеек нижней границы значений переменных, то есть $B$4:$E$4. Их также можно ввести путем выделения мышью непосредственно в экранной форме.
Рисунок 1.5. Ввод условия неотрицательности переменных задачи (1.1) Задание знаков ограничений ≤, ≥, = • Нажмите кнопку " Добавить " в окне " Добавление ограничения ". • В поле " Ссылка на ячейку " введите адрес ячейки левой части конкретного ограничения, например $F$10. Это можно сделать как с клавиатуры, так и путем выделения мышью нужной ячейки непосредственно в экранной форме. • В соответствии с условием задачи (1.1) выбрать в поле знака необходимый знак, например =. • В поле " Ограничение " введите адрес ячейки правой части рассматриваемого ограничения, например $H$10. • Аналогично введите ограничения: $F$11>=$H$11, $F$12<=$H$12. • Подтвердите ввод всех перечисленных выше условий нажатием кнопки OK. Окно " Поиск решения " после ввода всех необходимых данных задачи (1.1)–(1,2) представлено на рис.1.4. Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делают, нажав кнопки " Изменить " или " Удалить ". Решение задачи Установка параметров решения задачи Задача запускается на решение в окне " Поиск решения ". Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку " Параметры " и заполнить некоторые поля окна " Параметры поиска решения " (рис. 1.6).
Рисунок 1.6. Параметры поиска решения, подходящие для большинства задач ЛП Параметр " Максимальное время " служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов). Параметр " Предельное число итераций " служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767. Параметр " Относительная погрешность " служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации. Параметр " Допустимое отклонение " служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее. Параметр " Сходимость " применяется при решении нелинейных задач. Установка флажка " Линейная модель " обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода. Подтвердите установленные параметры нажатием кнопки "OK". Запуск задачи на решение Запуск задачи на решение производится из окна " Поиск решения " путем нажатия кнопки " Выполнить "(Solve). После запуска на решение задачи ЛП на экране появляется окно " Результаты поиска решения " с одним из сообщений, представленных на рис. 1.7, 1.8 и 1.9.
Рисунок 1.7. Сообщение об успешном решении задачи (Solver Found a Solution)
Рисунок 1.8. Сообщение при несовместной системе ограничений задачи
Рисунок 1.9. Сообщение при неограниченности ЦФ в требуемом направлении Иногда сообщения, представленные на рис. 1.8 и 1.9, свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует. Иногда слишком малое значение параметра " Относительная погрешность " не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д. В окне " Результаты поиска решения " представлены названия трех типов отчетов: " Результаты ", " Устойчивость ", " Пределы ". Они необходимы при анализе полученного решения на чувствительность (см. ниже 1.4). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) в экранной форме выбираем «Сохранить найденное решение» (Keep Solver Solution) и нажимаем кнопку "OK". После этого в экранной форме появляется оптимальное решение задачи (рис. 1.10).
Рисунок 1.10. Экранная форма задачи (1.1)–(1,2) после получения решения
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 366; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 –1,8 х 1+2 х 2+ х 3–4 х 4=756,
–1,8 х 1+2 х 2+ х 3–4 х 4=756,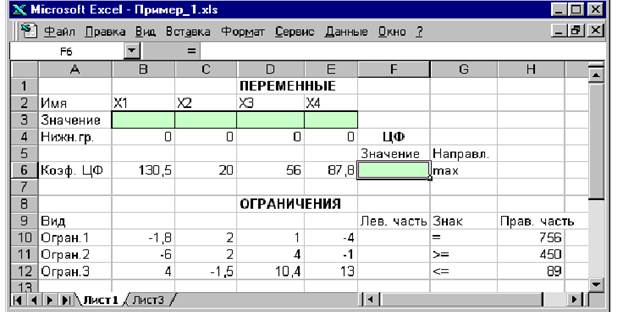 Рисунок 1.1. Экранная форма задачи (1.1)–(1,2) (курсор в ячейке F6)
Рисунок 1.1. Экранная форма задачи (1.1)–(1,2) (курсор в ячейке F6)

 (для версии 2010 кнопку Файл), а затем щелкните Параметры Excel. Выберите команду Надстройки и в окне Управление выберите пункт Надстройки Excel. Нажмите кнопку Перейти. В окне Доступные надстройки установите флажок Поиск решения, а затем нажмите кнопку ОК. Совет: если Поиск решения отсутствует в списке поля Доступные надстройки, то для проведения поиска нажмите кнопку Обзор.
(для версии 2010 кнопку Файл), а затем щелкните Параметры Excel. Выберите команду Надстройки и в окне Управление выберите пункт Надстройки Excel. Нажмите кнопку Перейти. В окне Доступные надстройки установите флажок Поиск решения, а затем нажмите кнопку ОК. Совет: если Поиск решения отсутствует в списке поля Доступные надстройки, то для проведения поиска нажмите кнопку Обзор.