
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Целевая Функция потребления.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ПОСТРОЕНИЕ ФУНКЦИИ СПРОСА Цель: используя методы моделирования с помощью целевой функции потребления научиться находить оптимальный набор благ потребителя, функции спроса на блага по цене, функции спроса по доходу с помощью ЭВМ. Рассмотрим некоторого потребителя, который потребляет некоторые блага Б1, Б2,…, Б n. Уровень удовлетворения потребностей потребителя обозначим через U. Пусть количество потребления каждого блага равно х 1, х 2, …, хn. Целевой функцией потребления называется зависимость U = U (x 1, x 2,..., xn). Каждый потребитель стремится максимизировать уровень удовлетворения потребностей, то есть U → max. Обозначим цену на единицу каждого блага через р 1, р 2,…, рn, а доход потребителя через D. Тогда должно выполняться бюджетное ограничение p 1 x 1 + p 2 x 2 +...+ pnxn ≤ D. В результате для нахождения оптимального набора благ необходимо решать задачу оптимального программирования: U (x 1, x 2,..., xn) → max, x 1, x 2,..., xn ≥ 0, p 1 x 1 + p 2 x 2 +...+ pnxn ≤ D. Рассмотрим методы ее решения на примере. ПРИМЕР 7.1. Пусть число благ равно трем, а функция потребления равна U (x 1, x 2, x 3) =
x 1, x 2, x 3≥ 0, 15 x 1 + 10 x 2 + 15 x 3≤500. Подготовим данные для решения задачи в Excel согласно рис. 7.1:
Рисунок 7.1 Исходные данные примера 7.1 Вводим в ячейку В4 «=КОРЕНЬ(B3*C3*D3)» (кавычки не вводить!), а в В5 «=B3*B2+C3*C2+D3*D2». Запускаем СЕРВИС/ПОИСК РЕШЕНИЯ. В ячейку «Установить целевую» устанавливаем ссылку на В4, флажок напротив надписи «Равной максимальному значению». После ставим курсор в поле «Изменяя ячейки» и обводим ячейки с переменными В3, С3 и D3. Для того чтобы ввести ограничения, нажимаем «Добавить», откроется окно «Добавление ограничения». В левом поле «Ссылка на ячейку» вводим ссылку на левую часть первого ограничения – ячейку В5, в центральном окне определяем знак «≤» и в правом «Ограничения» делаем ссылку на доход в D4. Для ввода второго ограничения вновь нажимаем «Добавить», ставим курсор в левое поле и обводим ячейки В3, С3 и D3 в среднем окне ставим «≥» и в правом число 0. Нажимаем «Выполнить», подтверждаем результаты, выбирая «Сохранить найденное решение» и «ОК», получаем результат: x 1 =11,1; x 2=16,7; x 3 =11,1; целевая функция равна 45,4 (рис.7.2).
Рисунок 7.2 Решение примера 7.1 Решим теперь задачу нахождения функции спроса по цене. Найдем, например, спрос на второе благо для разных цен на единицу этого блага. Будем задавать цену на второе благо от 5 до 15 и фиксировать спрос x 2 при этих ценах. Введем в столбец F цену блага, а в столбец G спрос на него. Ставим курсор в F1 и вводим подпись «Цена», а в ячейку G1 вводим подпись «Спрос». В соответствии с условием задачи, цена второго блага составляет 10 денежных единиц, в результате решения спрос на это благо составляет x 2 =16,7. Вводим в ячейку F7 значение цены 10, а в соседнюю G7 – спрос 16,7. Рассчитаем теперь спрос при цене 11. Исправляем в С2 значение на 11, вызываем СЕРВИС/ПОИСК РЕШЕНИЯ, нажимаем «Выполнить», подтверждаем результаты. Видим в ячейке С3 новое значение спроса – x 2 =15,2. Вводим в F8 число 11, в G8 число 15,2. Точно также (обязательно проделать на ЭВМ!) изменяем в С2 значения на 12, 13, 14 и 15, записав эти же значения в F9-F12, каждый раз запускаем надстройку «Поиск решения», получаем новые результаты в С3, записываем их вручную (не копированием, округляя до десятых) в G9-G12. Далее рассчитываем значения спроса для цены меньшей 10 единиц. Для этого изменяем в С2 значения на 5, 6, 7, 8 и 9, записав эти значения в F2-F6, каждый раз запускаем надстройку «Поиск решения», получаем новые результаты в С3, записываем их в G2-G6. В результате, при правильном выполнении всех действий, получаем следующие результаты:
Построим по полученным данным функцию спроса. Для этого ставим курсор в любую свободную ячейку, вызываем мастер диаграмм (ВСТАВКА/ДИАГРАММА), выбираем тип диаграммы «График», вид «График с маркерами» (левый второй сверху), нажимаем «Далее». Ставим курсор в поле «Диапазон» и обводим ячейки G2-G12. Переходим на закладку «Ряд» и ставим курсор в поле «Подписи оси Х», обводим ячейки F2-F12, нажимаем «Готово». Получаем график функции спроса по цене (рис.7.3).
Рисунок 7.3 График функции спроса по цене Точно также можно исследовать спрос и на первое и третье благо.
Найдем теперь функцию спроса по доходу на второе благо. Для этого будем менять доход в диапазоне 200-500 через 50 единиц, фиксируя спрос в ячейке С3. Вводим в H1 подпись «Доход», а в I1 подпись «Спрос». Исправляем в С2 цену на 10, а в D4 ставим доход 200. Вызываем и запускаем надстройку ПОИСК РЕШЕНИЯ. Видим, что спрос на второе благо равен 6,7. Вводим в H2 значение дохода 200, а спрос 6,7 вводим в I2. Далее, по аналогии, изменяем в D4 доход на 250, 300, 350, 400, 450, 500, 550, 600, занося эти данные в H3-H10, каждый раз запускаем надстройку ПОИСК РЕШЕНИЯ, полученный в С3 спрос вносим в ячейки I3-I10. При правильном расчете результаты будут 8,3; 10; 11,7; 13,3; 15; 16,7; 18,3; 20. По полученным данным, также как и для функции спроса по цене, строим график. Видно, что в данном случае график спроса по доходу прямая линия (рис.7.3).
Следует отметить, что можно построить функцию перекрестного спроса на одно благо по цене на другое. Задание 7.1. Четырехфакторную целевую функцию потребления U = U (x 1, x 2, x 3, x 4), цены на блага p 1, p 2, p 3, p 4, и доход D взять в соответствии с вариантом из таблицы. 1. Составив и решив задачу оптимального программирования, найти оптимальный набор благ. 2. Составить функцию спроса на второе благо от его цены, взяв 5 целых последовательных значений цены до и после той, какая указана в таблице. 3. Составить функцию спроса на третье благо по доходу, взяв по четыре значения дохода до и после указанной в таблице с шагом 50.
ПРИМЕЧАНИЕ: Для искомых количеств x 1, x 2, x 3, x 4 подготовить ячейки В3-Е3. В ячейке с целевой функцией В4 должна содержаться функция вида: 1. =LN(B3*C3*D3*E3) 16. =КОРЕНЬ(В3*С3)*D3*Е3 2. = B3*(C3+7)*D3*E3 17. =КОРЕНЬ(B3*С3)*D3*Е3 3. =СТЕПЕНЬ(B3*C3*D3*E3; 0,33) 18. =LN(B3*C3*D3*E3) 4. =КОРЕНЬ(B3)*C3*D3*E3 19. =B3*(C3+1)*D3*E3 5. =B3*C3*D3*(E3+3) 20. =B3*C3*(D3+5)*E3 6. =КОРЕНЬ(B3*D3)*С3*Е3 21. =КОРЕНЬ(D3)*B3*C3*E3 7. =LN(B3*C3*D3*E3) 22. =КОРЕНЬ(В3*С3)*D3*Е3 8. = B3*(C3+7)*D3*E3 23. =КОРЕНЬ(B3*С3)*D3*Е3 9. =СТЕПЕНЬ(B3*C3*D3*E3; 0,33) 24. =LN(B3*C3*D3*E3) 10. =КОРЕНЬ(B3)*C3*D3*E3 25. =B3*(C3+1)*D3*E3 11. =B3*C3*D3*(E3+3) 26. =B3*C3*(D3+5)*E3 12. =КОРЕНЬ(B3*D3)*С3*Е3 27. =КОРЕНЬ(D3)*B3*C3*E3 13. =КОРЕНЬ(B3)*C3*D3*E3 28. =B3*(C3+1)*D3*E3 14. =B3*C3*D3*(E3+3) 29. =B3*C3*(D3+5)*E3 15. =КОРЕНЬ(B3*D3)*С3*Е3 30. =КОРЕНЬ(D3)*B3*C3*E3 Отчет должен содержать оптимальный набор благ x 1, x 2, x 3, x 4, график функции спроса на второе благо от его цены x 2(p 2) и график функции спроса на третье благо по доходу x 3(D).
Работа № 8 БАЛАНСОВЫЕ МОДЕЛИ Цель: рассмотреть методы решения задач межотраслевого анализа на ЭВМ используя модель Леонтьева. Балансовые модели предназначены для определения равновесного баланса между производством, потреблением и реализацией во внешнюю сферу продукции нескольких взаимосвязанных отраслей. Рассмотрим решение межотраслевого баланса на ЭВМ в соответствии с моделью Леонтьева на следующем примере. Имеется баланс трех взаимосвязанных отраслей за предыдущий период:
1. Найти валовой продукт каждой отрасли, чистую продукцию каждой отрасли, матрицу коэффициентов прямых затрат. 2. Какой будет конечный продукт каждой отрасли, если валовой станет равен, соответственно, 100, 150 и 200. 3. Какой будет валовой продукт каждой отрасли, если конечный продукт первой отрасли необходимо увеличить на 50%, второй уменьшить на 4 единицы, а третьей увеличить на 6 единиц. Подготавливаем таблицу исходных данных в электронной таблице Excel.
1. Для нахождения валового продукта каждой отрасли в ячейку F3 вводим формулу «=СУММ(В3:Е3)» (для ее ввода достаточно нажать кнопку автосуммы со значком S). Результат – 124. Автозаполнением переносим результат ячейки на F4 и F5. Для расчета чистой прибыли вводим в ячейку В6 формулу «=F3-B3-B4-B5», в С6 формулу «=F4-C3-C4-C5», в D6 формулу «=F5-D3-D4-D5». Находим коэффициенты прямых затрат. Для этого каждый столбец матрицы В3-D5 нужно разделить на соответствующий валовой продукт. В ячейку В7 вводим «=B3/$F$3» (чтобы сделать абсолютную ссылку $F$3 нужно щелкнуть по ячейки F3 и нажать клавишу F4). Автозаполняем В7 на В8 и В9. Аналогично вводим в С7 «=C3/$F$4» и автозаполняем на С8 и С9. Вводим в D7 «=D3/$F$5» и автозаполняем на D8 и D9. Матрица коэффициентов затрат рассчитана. 2. Так как новый валовой продукт каждой отрасли равен, соответственно, 100, 150 и 200, то вводим эти числа в ячейки Н3, Н4 и Н5. По формуле, новый конечный продукт равен Y = (E – A) X. Для ее использования вводим единичную матрицу. В А12 вводим подпись «Е=», а в В11-D13 вводим числа 1 0 0 0 1 0 0 0 1. Рассчитываем матрицу (Е-А). Вводим в А16 подпись «(Е-А)=», а в В15 «=B11-B7». Автозаполняем ячейку на В15-D17. Для вычисления результата – новых значений конечного продукта в ячейку G3 вводим функцию перемножения матриц – МУМНОЖ (категория Математические»). Аргументы функции: в поле «массив 1» даем ссылку B15:D17 (матрица Е-А), в поле «массив 2» – H3:H5 (новый валовой продукт). Далее обводим ячейки G3-G5 курсором мыши, выделяя их, и нажимаем F2 и Ctrl+Shift+Enter. Результат – новый конечный продукт.
3. Если конечный продукт первой отрасли нужно увеличить на 50%, то он станет 124,5, если второй уменьшить на 4, то он станет 93, если третий увеличить на 6 единиц, он будет 138. Вводим в ячейки G7-G9 числа 124,5; 93; 138. В соответствии с формулой Леонтьева новый валовой продукт находим по формуле X = (E – A)–1 Y. Для расчета обратной матрицы в ячейку Е16 вводим подпись «(Е–А) обрат.», а в F15 ставим формулу расчета обратной матрицы МОБР (категория «Математические»). Аргумент функции – ссылка на B15-D17. Обводим курсором ячейки F15-H17 и нажимаем F2 и Ctrl+Shift+Enter. Для вычисления новых значений валового продукта в ячейку Н7 вводим функцию перемножения матриц – МУМНОЖ. Аргументы: в поле «массив 1» даем ссылку F15:H17, в поле «массив 2» – G7:G9. Далее обводим ячейки Н7-Н9 и нажимаем F2 и Ctrl+Shift+Enter. Результат – новый валовой продукт. Задача решена.
Задание 8.1. Решить задачу межотраслевого баланса производства и распределения продукции для 4 отраслей. Матрица межотраслевых материальных связей xij и вектор валового выпуска Xj приведены в таблице по вариантам.
1. Найти конечный продукт каждой отрасли, чистую продукцию каждой отрасли, матрицу коэффициентов прямых затрат.
2. Какой будет конечный продукт каждой отрасли, если валовой продукт первой отрасли увеличится в 2 раза, у второй увеличится на половину, у третьей не изменится, у четвертой – уменьшится на 10 процентов. 3. Найти валовой продукт, если конечный станет равен 700, 500, 850 и 700. Отчет должен содержать полную балансовую таблицу для четырех отраслей, конечный продукт каждой отрасли при изменении валового, валовой продукт каждой отрасли при изменении конечного.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ 1. Гельруд Я.Д. Экономико-математические методы (электронный вариант). –Челябинск.: ЧелГУ. 2010. – 421с. 2. Кремер Н.Ш. Исследование операций в экономике. – М.: ЮНИТИ, 2005. – 407с. 3. Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем: Учебное пособие. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2006. – 368с. 4. Вентцель Е.С. Исследование операций: Задачи, принципы, методология. –М.: Высшая школа, 2005. – 208 с. 5. Моделирование экономических процессов: Учебник для студентов вузов, обучающихся по специальностям экономики и управления (060000) / Под ред. М.В. Грачёвой, Л.Н. Фадеевой, Ю.И. Черемных. М.: ЮНИТИ-ДАНА, 2005. –351 с. 6. Фомин Г.П. Математические методы и модели в коммерческой деятельности: Учебник. –2‑е изд. М.: Финансы и статистика, 2005. –616 с. 7. Шелобаев С.И. Математические методы и модели в экономике, финансах, бизнесе: Учеб. пособие для вузов. –2‑е изд. М.: ЮНИТИ-ДАНА, 2005. –287 с. 8. Гельруд Я.Д. Модели и методы управления проектами в условиях риска и неопределенности. –Челябинск.: ЮУрГУ. 2006. – 220 с. 9. Куправа Т.А. EXCEL. Практическое руководство. - Диалог-МИФИ, Москва, 2004. - 242 с. 10. Excel 2007. Руководство менеджера проекта. Хелдман К., Хелдман У. -: Эксмо, Формат: DJVU, Размер: 54МБ,2008. - 448с. * В табл. 1 указывается название тем для изучения, их краткое содержание и объем занятий по видам учебной работы в часах. (Название разделов и тем указывается в соответствии с обязательным минимумом содержания дисциплины по ГОС)
**(Указывается краткое содержание разделов и тем дисциплины. При необходимости даются методические рекомендации и указания по изучению данных разделов и тем.) *** Л- лекции ПЗ- практические занятия ЛР- лабораторная работа СРС- самостоятельная работа студента
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 563; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.35.75 (0.013 с.) |

 . Предположим, что цена на единицу первого блага равна 15, второго 10 и третьего 15, а доход потребителя составляет 500. Тогда задача примет вид:
. Предположим, что цена на единицу первого блага равна 15, второго 10 и третьего 15, а доход потребителя составляет 500. Тогда задача примет вид: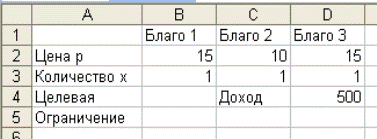

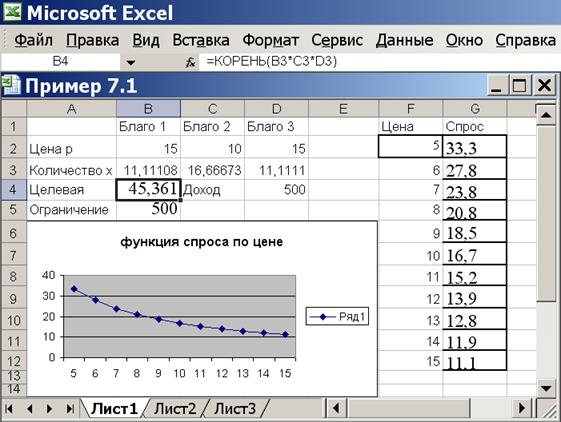
 Рисунок 7.4 График функции спроса по доходу
Рисунок 7.4 График функции спроса по доходу x 3 x 4
x 3 x 4

 x 2 x 3 x 4
x 2 x 3 x 4
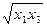 x 2 x 4
x 2 x 4
 x 1 x 2 x 4
x 1 x 2 x 4





