Решение задач многокритериальной оптимизации на эвм

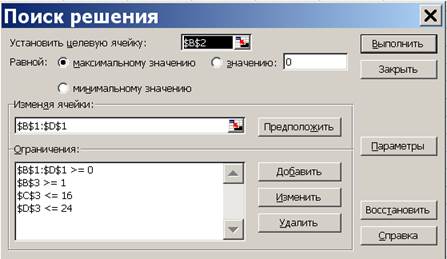
Цель: научиться методам решения многокритериальных ЗЛП с помощью ЭВМ, используя метод последовательных уступок.

Во многих реальных экономических задачах критериев, которые оптимизируются, может быть несколько. Например, при производстве продукции максимизируется качество и минимизируется себестоимость, при взятии ссуды в банке максимизируется кредитный срок и минимизируется процентная ставка, при выборе места для строительства дома отдыха максимизируются экологические условия и минимизируется расстояние от населенного пункта и пр.

Существует несколько методов решения многокритериальных задач. Одним из наиболее эффективных является метод последовательных уступок, использование которого рассмотрим на примере.

ПРИМЕР 4.1. Математическая модель трехкритериальной задачи имеет вид:

Z ₁=2 x ₁+ x ₂– 3 x ₃→max;

Z ₂= x ₁+ 3 x ₂– 2 x ₃→min;

Z ₃= – x ₁+ 2 x ₂+4 x ₃→max;

x ₁+ 3 x ₂+2 x ₃≥1,

2 x ₁– x ₂+ x ₃≤16,

x ₁+ 2 x ₂≤24,

x ₁, x ₂, x ₃ ≥ 0.

Решить задачу методом последовательных уступок, выбрав уступку по первому критерию d1=4, а по второму d2=5.

Открываем электронную книгу Excel и, как и для решения однокритериальной задачи определяем ячейки под переменные x ₁, x ₂, x ₃. Для этого в ячейку А1 вводим подпись «Переменные», а соседние три ячейки В1, С1 и D1 вводим значения переменных. Это могут быть произвольные числа, например единицы, далее они будут оптимизироваться. Во второй строке задаем целевые функции. В А2 вводим подпись «Целевые», а в В2 формулой «=2*B1+C1–3*D1» задаем первую целевую функцию 2 x ₁+ x ₂–3 x ₃. Аналогично в С2 и D2 вводим вторую и третью целевую функцию, вводя в С2 «=B1+3*C1–2*D1», а в D2 «= –B1+2*C1+4*D1». В третью строку вводим левые части ограничений. Для этого вводим в А3 подпись «Ограничения», в В3 формулу «=B1+3*C1+2*D1», в С3 формулу «=2*B1–C1+D1» и в D3 формулу «=B1+2*C1».

Предварительные действия завершены. Вызываем надстройку «Поиск решения» в меню «Сервис». На первом этапе оптимизируем первую целевую функцию.

После открытия окна «Поиск решения» в поле «Установить целевую» ставим курсор и делаем ссылку на ячейку В2, щелкая по ней мышью. В окне появится $B$2. В связи с тем, что целевая функция максимизируется, далее нужно проверить, что флажок ниже поля стоит напротив надписи «Равной максимальному значению». После ставим курсор в поле «Изменяя ячейки» и обводим ячейки с переменными В1, С1 и D1, выделяя ячейки с переменными. В поле появится $B$1:$D$1. В нижней части окна находится поле «Ограничения». Для того чтобы ввести ограничения, нажимают кнопку «Добавить», откроется окно «Добавление ограничения». В левом поле «Ссылка на ячейку» вводят ссылку на левую часть первого ограничения – ячейку В3, в центральном окне определяем знак ≥ и в правом «Ограничения» набираем правую часть ограничения – число 1. Нажимаем «ОК», видим, что ограничение появилось в окне. Нажимаем вновь «Добавить», вводим «С3» «≤» и «16». Вновь нажимаем «Добавить», вводим «D3» «≤» и «24». Для ввода дополнительных ограничений x ₁, x ₂, x ₃ ≥ 0 вновь нажимаем «Добавить», ставим курсор в левое поле и обводим ячейки В1, С1 и D1 (результат $B$1:$D$1) в среднем окне ставим «≥» и в правом число 0. Результат на рис.4.1.

Рисунок 4.1 Окно «Поиск решения» первого этапа

Для запуска вычислений нажимаем кнопку «Выполнить». Появляется надпись, что решение найдено. Выбираем «Сохранить найденное решение» и нажимаем «ОК» – видим результат (рис. 4.2): в ячейках В1, С1 и D1 значения переменных x ₁, x ₂, x ₃, соответствующие оптимальному решению: 11,2; 6,4 и 0. В ячейки В2 – значение целевой функции 28,8.

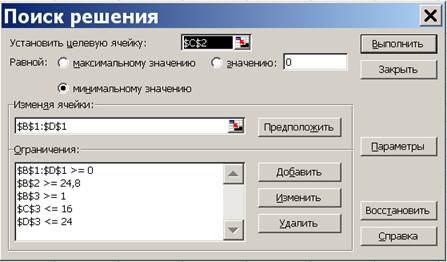
Рисунок 4.2 Решение первого этапа примера 4.1

На втором этапе оптимизируется вторая целевая функция. При этом первую, в соответствие с методом последовательных уступок, можно ухудшить на величину не более чем d1=4. По этой причине, на втором шаге, значения в ячейке В2 (где хранится первая целевая функция, которая максимизируется) может быть не меньшее, чем 28,8–4=24,8. Вызываем надстройку «Сервис/Поиск решения», видим, что все прежние данные остались введенными. Меняем ссылку на целевую функцию. Ставим курсор в поле «Установить целевую» и щелкаем по ячейке С2, в которой находится ссылка на вторую целевую функцию. Так как вторая целевая функция минимизируется, то ставим флажок в поле напротив надписи «Равной минимальному значению». Вводим дополнительное ограничение, связанное с уступкой по первому критерию. Переводим курсор в поле «Ограничения» и нажимаем кнопку «Добавить». В появившемся окне «Добавление ограничения» в трех окнах (слева направо) вводим данные «В2», «≥», «24,8». Результат на рис.4.3.

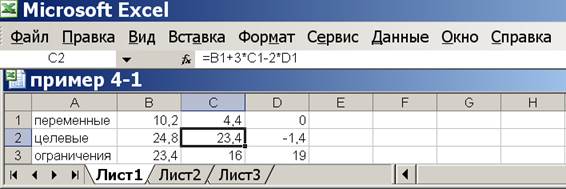
Рисунок 4.3 Окно «Поиск решения» второго этапа

Для запуска вычислений нажимаем кнопку «Выполнить». Появляется надпись, что решение найдено. Выбираем «Сохранить найденное решение» и нажимаем «ОК» – видим результат (рис. 4.4): переменные x ₁, x ₂, x ₃равны 10,2; 4,4; 0. Вторая целевая функция равна 23,4 (ячейка В2). Первая равна своему минимальному значению 24,8 (ячейка С2).

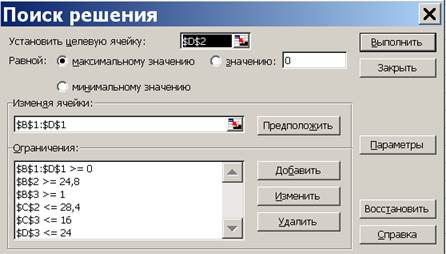
Рисунок 4.4 Решение второго этапа примера 4.1

На третьем этапе делаем уступку по второму критерию. Величина уступки равна d2=5. Так, как вторая функция минимизируется, то ее значение не должно превышать 23,4+5=28,4. Вызываем надстройку «Сервис/Поиск решения». Меняем ссылку на целевую функцию. Ставим курсор в поле «Установить целевую» и щелкаем по ячейке D2, в которой находится ссылка на третью целевую функцию. Так как третья целевая максимизируется, то ставим флажок в поле напротив надписи «Равной максимальному значению». Вводим дополнительное ограничение, связанное с уступкой по второму критерию. Переводим курсор в поле «Ограничения» и нажимаем кнопку «Добавить». В появившемся окне «Добавление ограничения» вводим данные «С2», «≤», «28,4». Результат на рис.4.5.

Рисунок 4.5 Окно «Поиск решения» третьего этапа

Для запуска вычислений нажимаем кнопку «Выполнить». Появляется надпись, что решение найдено. Выбираем «Сохранить найденное решение» и нажимаем «ОК» – видим результат (рис. 4.6): переменные x ₁, x ₂, x ₃равны 10,76; 6,62; 1,11. Целевые функции равны, соответственно, 24,8; 28,4 и 6,93. Это окончательный ответ. Все дополнительные условия соблюдены.

Рисунок 4.6 Окончательное решение примера 4.1

Задание 4.1. Решить методом последовательных уступок двухкритериальную задачу, представленную математической моделью:

Z ₁= x ₁–3 x ₂→ max;

Z ₂= а x ₁–2 x ₂→ min;

3 x ₁+ 5 x ₂≥2,

x ₁+ x ₂≤11,

x ₁– x ₂≤ –1,

x ₁, x ₂ ≥ 0.

Уступка по первому критерию оптимизации d1 = 2.

Значение неизвестного параметра а взять равным номеру варианта.

Отчет должен содержать оптимальные значения переменных и всех целевых функций, полученных в результате расчета на ЭВМ.

Задание 4.2. Молочный комбинат, исследовав конъюнктуру местного рынка, решил выпускать новый вид йогурта, который был бы конкурентно способен. При этом необходимо разработать план организации производства для выпуска данного продукта. Основными затратами на разработку являются затраты на модернизацию оборудование х и затраты на научные исследования у. При исследовании установлено, что себестоимость единицы продукции при этом будет зависеть от затрат как F ₁ (x, y) = 12 + a x + (31 - а) y, а качество продукции как F ₂ = 6 + (31 - а) x + а y. Ставится задача минимизировать себестоимость (цену) данного продукта и максимизировать качество выпускаемой продукции. Из двух целевых функций основной считается цена (себестоимость продукции). По фактору «цена» можно сделать уступку 3 денежные единицы. Решить задачу методом последовательных уступок и найти оптимальные значения факторов х и у, а также значения целевых функций, если на факторы наложены ограничения:

2 х+у ≥ 8;

5 х+ 4 у ≤40;

0≤ х ≤6; у≥ 0.

Значение неизвестного параметра а взять равным номеру варианта.

Отчет должен содержать математическую модель задачи, оптимальные значения переменных и всех целевых функций, полученных в результате расчета на ЭВМ, выводы, какие должны быть затраты на модернизацию оборудования и на научные исследования, какими при этом будет себестоимость и качество продукции.

Задание 4.3. Решить методом последовательных уступок двухкритериальную задачу, представленную математической моделью:

Z ₁=2 x ₁+ x ₂– 5 x ₃→ max;

Z ₂=3 x ₁+ 2 x ₂– 4 x ₃→ min;

4 x ₁+ 6 x ₂+5 x ₃≥2,

–2 x ₁+ x ₂–3 x ₃≤27,

6 x ₁+ 5 x ₂≤75,

2 x ₁+ 3 x ₃≥3,

x ₁ ,x ₂ ,x ₃ ≥ 0.

Уступка по первому критерию оптимизации d1 равна номеру варианта а.

Отчет должен содержать оптимальные значения переменных и всех целевых функций, полученных в результате расчета на ЭВМ.

Задание 4.4. Решить методом последовательных уступок трехкритериальную задачу, представленную математической моделью:

Z ₁= – x ₁+3 x ₂– 2 x ₃→ min;

Z ₂=–3 x ₁+ 2 x ₂– x ₃→ max;

Z ₃= x ₁+ 2 x ₂+4 x ₃→ max;

3 x ₁+ 2 x ₂+ a x ₃≥1,

x ₁+ а x ₂+ x ₃≤19,

а x ₁+ 3 x ₂≤21,

x ₁ ,x ₂ ,x ₃ ≥ 0.

Значение неизвестного параметра а взять равным номеру варианта.

Уступки по первому и второму критерию оптимизации равны d1 = 6,d2 = 4.

Отчет должен содержать оптимальные значения переменных и всех целевых функций, полученных в результате расчета на ЭВМ.

Работа № 5