Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экономико-математических методов и моделейСтр 1 из 8Следующая ⇒
МИНИСТЕРСТВО НАУКИ И ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ЧЕЛЯБИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» Кафедра
ГЕЛЬРУД Я.Д.
ПРАКТИКУМ ПО ПРИМЕНЕНИЮ ЭКОНОМИКО-МАТЕМАТИЧЕСКИХ МЕТОДОВ И МОДЕЛЕЙ В ТАМОЖЕННОЙ СТАТИСТИКЕ
Учебно-методический комплекс
Челябинск Гельруд Я.Д. Практикум по применению экономико-математических методов и моделей в таможенной статистике: Учебно-методический комплекс. – Челябинск: Изд. ЧелГУ, 2011. – 68с. Учебно-методический комплекс (УМК) по дисциплине «Практикум по применению экономико-математических методов и моделей в таможенной статистике» предназначен для студентов, обучающихся по специальности «Таможенное дело». УМК включает: рабочую программу дисциплины, календарно-тематический план для самостоятельной работы студентов, практикум, содержащий примеры решения типовых задач, задания для контрольной работы по каждой теме и список общедоступной учебной и справочной литературы. В практикуме достаточно подробно демонстрируется применение математического аппарата для решения конкретных экономических задач при обработке таможенной статистики.
УМК рассмотрен и рекомендован к публикации на заседании кафедры «Экономика отраслей и рынков».
Протокол № от 2011г
Зав. кафедрой Бархатов В.И.
ОГЛАВЛЕНИЕ ВВЕДЕНИЕ ……………………………………………………………………..4 РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ………………………………..7 МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ…………………………………… 10 РАБОТА № 1 Методы решения задач линейного программирования на ЭВМ…………….12 РАБОТА № 2 Двухиндексные задачи ЛП (транспортная задача)…………………………...33 РАБОТА № 3. Решение двойственных задач и задач нелинейного программирования …...37 РАБОТА № 4 Решение задач многокритериальной оптимизации на ЭВМ ………….……..41 РАБОТА № 5 Экономическое моделирование методами теории игр …………..…………. 47 РАБОТА № 6 Игры с природой ………………………………………………..………..... …..54 РАБОТА № 7 Целевая функция потребления. Построение функции спроса ………….. ….59
РАБОТА № 8 Балансовые модели ……………………………………………………..……...64 СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ. ….……………………..68
ВВЕДЕНИЕ Дисциплина «Практикум по применению экономико-математических методов и моделей» является региональной (вузовской) компонентой. Научно-исследовательская и практическая работа современного экономиста немыслима без применения математических моделей и компьютерных технологий. Целью данного углубленного математического образования является: - приобретение практических навыков по решению конкретных задач управления бизнесом на основе применения современных экономико-математических методов, адекватных специфике ведения бизнеса в условиях постиндустриального информационного общества, отличающейся высокой степенью неопределённости и хозяйственных рисков, остротой конкурентной борьбы, высоким уровнем производительности труда и сопряжёнными с ним проблемами распределения общественного продукта, ускоренными темпами внедрения и распространения инноваций. Задачи дисциплины:
В ходе изучения дисциплины «Практикум по применению экономико-математических методов и моделей» студент должен знать:
владеть:
иметь представление:
уметь:
Данная дисциплина является практическим закреплением дисциплины «Математические методы в исследовании экономики».
РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ
Содержание программы В дисциплине "Практикум по применению экономико-математических методов и моделей" рассматриваются задачи о связях экономических явлений, условия и методы построения экономических моделей, методы нахождения оптимальных решений в экономике. Теоретические материалы по математическим методам в экономике содержатся в [1]. Кроме того, в [2-8] приведен список дополнительной литературы для более полного освоения дисциплины. Практикум включает в себя восемь работ по основным темам, предусмотренным учебной программой по дисциплине: различные виды задач линейного и нелинейного программирования, теория двойственности и ее применение в экономическом анализе, многокритериальные оптимизационные задачи, задачи теории матричных игр и игры с природой, моделирование спроса и балансовые модели. Каждая работа содержит описательную часть, примеры решения поставленных задач на ЭВМ и задания для самостоятельного решения по вариантам. Номер варианта соответствует номеру студента в списке группы. В работе №1 используемый аппарат Excel разбирается весьма подробно, каждый шаг иллюстрируется, приводятся команды и названия всех опций на русском и английском языках (для пользователей англоязычной версии Excel), в последующих работах решение задач излагается менее детально, такого же стиля изложения следует придерживаться при самостоятельном выполнении заданий. В [9-10] приведен список популярных справочников по Excel. Рабочая программа Практикум по применению экономико-математических методов и моделей (очная форма обучения) Темы занятий** Таблица 1. Разделы дисциплины, виды и объем занятий
Содержание тем дисциплины.
Решение основных типов задач линейного программирования на ЭВМ – определение оптимального ассортимента продукции, задача составления смеси, целочисленные задачи, в том числе задачи с булевыми переменными. Тема 2. Двухиндексные задачи ЛП (транспортная задача). Решение основных типов двухиндексных задач линейного программирования на ЭВМ – транспортная задача, задача о назначении. Тема 6. Игры с природой Методы принятия решений в условиях неопределенности и риска на ЭВМ с использованием критериев Лапласа, Вальда, Байеса, Сэвиджа и Гурвица. Тема 8. Балансовые модели Методы решения задач межотраслевого анализа на ЭВМ используя модель Леонтьева.
Формы контроля Текущий контроль осуществляется в форме решения практических задач, анализа итогов участия слушателей (студентов) на семинарских занятиях и практикумах. Итоговый контроль по всему объему дисциплины проводится в форме защиты итоговой контрольной работы и экзамена. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ Методические рекомендации по решению практических задач. Основная цель семинарских занятий – получение практических навыков решения конкретных задач и примеров по основным разделам математической экономики. Решение предлагаемых практических заданий является средством текущего контроля приобретенных при самостоятельной работе знаний и навыков студентов, а также необходимо для самооценки студентами их подготовленности по каждой теме.
Методические рекомендации по выполнению контрольных работ. Контрольная работа является важной частью итогового контроля знаний и навыков студентов по всем темам. При выполнении работы студент учится работать со специальной литературой, обрабатывать полученную информацию, творчески ее использовать.
Также как и при выполнении практических заданий, изложение решений контрольной работы должно быть кратким, не загромождено текстовыми формулировками используемых утверждений и определений; простые преобразования и арифметические выкладки пояснять не следует. Степень подробности изложения решений контрольной работы должна соответствовать степени подробности решения примеров в соответствующих разделах теоретических материалов. Ключевые идеи решения следует обосновывать ссылкой на использованные утверждения и приводить номера соответствующих формул. Задания для итоговой контрольной работы. Задания для итоговой контрольной работы содержатся в соответствующих разделах. Номер варианта выбирается по номеру студента в списке группы. Требования к критериям оценки выполнения контрольных работ. Контрольная работа предназначена для итогового контроля знаний и навыков студентов по всем темам. Оценка за каждую задачу контрольной работы - зачтено или не зачтено. Оценка зачтено ставится за правильное и полное решение задачи, допускаются небольшие погрешности в изложении и вычислениях. Оценка за контрольную работу – зачтено, если зачтены все контрольные задания по всем темам. Если контрольная работа не зачтена, то студент должен выполнить работу над ошибками и затем заново написать другой вариант контрольной работы, который укажет преподаватель. Методические рекомендации по организации самостоятельной работы студентов Успешное освоение дисциплины требует напряжённой самостоятельной работы студентов. При подготовке к занятиям и контрольным работам студенты кроме теоретических материалов изучают рекомендованную литературу. Для самостоятельного изучения студентам предлагаются следующие темы. Моделирование задач принятия решений [3,5]. Матричные игры, игры с природой [7, с.294], [8, с.217], [2, с.173]. [6]. Графы и сетевые графики [5, с.137], [2, с. 286]. Управление проектами в условиях риска и неопределенности [8].
РАБОТА № 1 Ввод исходных данных Создание экранной формы и ввод в нее условия задачи Экранная форма для ввода условий задачи (1.1)–(1,2) вместе с введенными в нее исходными данными представлена на рис.1.1.
В экранной форме на рис.1.1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Так, например, переменным задачи (1.1) соответствуют ячейки B3(х 1), C3(х 2), D3(х 3), E3(х 4), коэффициентам ЦФ соответствуют ячейки B6(с 1=130,5), C6(с 2=20), D6(с 3=56), E6(c 4=87,8), правым частям ограничений соответствуют ячейки H10(b 1=756), H11(b 2=450), H12(b 3=89) и т.д. Ввод зависимостей из математической модели в экранную форму Зависимость для ЦФ В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Значение ЦФ определяется выражением (1.2)
Используя обозначения соответствующих ячеек в Excel (см. рис.1.1), формулу для расчета ЦФ (1.2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3, D3, E3), на соответствующую ячейку, отведенную для коэффициентов ЦФ (B6, C6, D6, E6). Чтобы задать эту формулу необходимо в ячейку F6 ввести следующее выражение и нажать клавишу "Enter" =СУММПРОИЗВ(B$3:E$3;B6:E6), (1.3) где символ $ перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится; символ: означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия (например, запись B6:E6 указывает на ячейки B6, C6, D6 и E6). После этого в целевой ячейке появится 0 (нулевое значение) (рис. 1.2).
Рисунок 1.2. Экранная форма задачи (1.1)–(1,2) после ввода всех необходимых формул (курсор в ячейке F6) Примечание 1. Существует другой способ задания функций в Excel с помощью режима "Вставка функций", который можно вызвать из меню "Вставка" или при нажатии кнопки " fх " на стандартной панели инструментов. Так, например, формулу (1.3) можно задать следующим образом: • курсор в поле F6; • нажав кнопку " fх ", вызовите окно "Мастер функций – шаг 1 из 2"; • выберите в окне "Категория" категорию "Математические"; • в окне "Функция" выберите функцию СУММПРОИЗВ; • в появившемся окне "СУММПРОИЗВ" в строку "Массив 1" введите выражение B$3:E$3, а в строку "Массив 2" – выражение B6:E6 (рис.1.3); • после ввода ячеек в строки "Массив 1" и "Массив 2" в окне "СУММПРОИЗВ" появятся числовые значения введенных массивов (см. рис.1.3), а в экранной форме в ячейке F6 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).
Рисунок 1.3. Ввод формулы для расчета ЦФ в окно "Мастер функций" Зависимости для левых частей ограничений Левые части ограничений задачи (1.1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3, D3, E3), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B10, C10, D10, E10 – 1-е ограничение; B11, C11, D11, E11 – 2-е ограничение и B12, C12, D12, E12 – 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл. 1. Формулы, описывающие ограничения модели (1.1) Таблица 1
Как видно из табл. 1, формулы, задающие левые части ограничений задачи (1.1), отличаются друг от друга и от формулы (1.3) в целевой ячейке F6 только номером строки во втором массиве. Этот номер определяется той строкой, в которой ограничение записано в экранной форме. Поэтому для задания зависимостей для левых частей ограничений достаточно скопировать формулу из целевой ячейки в ячейки левых частей ограничений. Для этого необходимо: • поместить курсор в поле целевой ячейки F6 и скопировать в буфер содержимое ячейки F6 (клавишами "Ctrl-Insert"); • помещать курсор поочередно в поля левой части каждого из ограничений, то есть в F10, F11 и F12, и вставлять в эти поля содержимое буфера (клавишами "Shift-Insert") (при этом номер ячеек во втором массиве формулы будет меняться на номер той строки, в которую была произведена вставка из буфера); • на экране в полях F10, F11 и F12 появится 0 (нулевое значение) (см. рис.1.2). Задание ЦФ Дальнейшие действия производятся в окне "Поиск решения" (Solver Add-in), которое для версии 2003 вызывается из меню "Сервис". Для первоначальной активации опции "Поиск решения" в меню "Сервис" нажмите «Надстройки», в появившемся окне отметьте "Поиск решения" и нажмите «ОК». Далее действуйте по инструкции. Для версии 2007 щелкните значок Кнопка Microsoft Office В случае появления сообщения о том, что пакет Поиск решения не установлен на компьютере и предложения установить его, нажмите кнопку Да. После загрузки в версии 2003 команда Поиск решения становится доступной в пункте Сервис, а в версии 2007 и 2010 на вкладке Данные. После завершения генерации вызывайте " Поиск решения " (рис. 1.4) и: • поставьте курсор в поле " Установить целевую "(Set Target Cell); • введите адрес целевой ячейки $F$6 или сделайте одно нажатие левой клавиши мыши на целевую ячейку в экранной форме – это будет равносильно вводу адреса с клавиатуры; • введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке " Равной: максимальному значению "(Equal to … Max … Value of:).
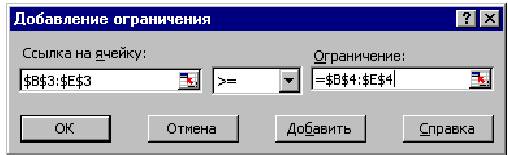
Рисунок 1.4. Окно " Поиск решения " задачи (1.1)–(1,2) Ввод ограничений и граничных условий Задание ячеек переменных В окно " Поиск решения " в поле " Изменяя ячейки " (By Changing Cell) впишите адреса $B$3:$E$3. Необходимые адреса можно вносить в поле " Изменяя ячейки " и автоматически путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме. Задание граничных условий для допустимых значений переменных В нашем случае на значения переменных накладывается только граничное условие неотрицательности, то есть их нижняя граница должна быть равна нулю (см. рис. 1.1). • Нажмите кнопку " Добавить "(Add), после чего появится окно " Добавление ограничения " (Add Constraints) (рис. 1.5). • В поле " Ссылка на ячейку "(Cell Reference) введите адреса ячеек переменных $B$3:$E$3. Это можно сделать как с клавиатуры, так и путем выделения мышью всех ячеек переменных непосредственно в экранной форме. • В поле знака откройте список предлагаемых знаков и выберите ≥. • В поле " Ограничение " (Subject to the Constraints) введите адреса ячеек нижней границы значений переменных, то есть $B$4:$E$4. Их также можно ввести путем выделения мышью непосредственно в экранной форме.
Рисунок 1.5. Ввод условия неотрицательности переменных задачи (1.1) Задание знаков ограничений ≤, ≥, = • Нажмите кнопку " Добавить " в окне " Добавление ограничения ". • В поле " Ссылка на ячейку " введите адрес ячейки левой части конкретного ограничения, например $F$10. Это можно сделать как с клавиатуры, так и путем выделения мышью нужной ячейки непосредственно в экранной форме. • В соответствии с условием задачи (1.1) выбрать в поле знака необходимый знак, например =. • В поле " Ограничение " введите адрес ячейки правой части рассматриваемого ограничения, например $H$10. • Аналогично введите ограничения: $F$11>=$H$11, $F$12<=$H$12. • Подтвердите ввод всех перечисленных выше условий нажатием кнопки OK. Окно " Поиск решения " после ввода всех необходимых данных задачи (1.1)–(1,2) представлено на рис.1.4. Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делают, нажав кнопки " Изменить " или " Удалить ". Решение задачи Установка параметров решения задачи Задача запускается на решение в окне " Поиск решения ". Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку " Параметры " и заполнить некоторые поля окна " Параметры поиска решения " (рис. 1.6).
Рисунок 1.6. Параметры поиска решения, подходящие для большинства задач ЛП Параметр " Максимальное время " служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов). Параметр " Предельное число итераций " служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767. Параметр " Относительная погрешность " служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации. Параметр " Допустимое отклонение " служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее. Параметр " Сходимость " применяется при решении нелинейных задач. Установка флажка " Линейная модель " обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода. Подтвердите установленные параметры нажатием кнопки "OK". Запуск задачи на решение Запуск задачи на решение производится из окна " Поиск решения " путем нажатия кнопки " Выполнить "(Solve). После запуска на решение задачи ЛП на экране появляется окно " Результаты поиска решения " с одним из сообщений, представленных на рис. 1.7, 1.8 и 1.9.
Рисунок 1.7. Сообщение об успешном решении задачи (Solver Found a Solution)
Рисунок 1.8. Сообщение при несовместной системе ограничений задачи
Рисунок 1.9. Сообщение при неограниченности ЦФ в требуемом направлении Иногда сообщения, представленные на рис. 1.8 и 1.9, свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует. Иногда слишком малое значение параметра " Относительная погрешность " не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д. В окне " Результаты поиска решения " представлены названия трех типов отчетов: " Результаты ", " Устойчивость ", " Пределы ". Они необходимы при анализе полученного решения на чувствительность (см. ниже 1.4). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) в экранной форме выбираем «Сохранить найденное решение» (Keep Solver Solution) и нажимаем кнопку "OK". После этого в экранной форме появляется оптимальное решение задачи (рис. 1.10).
Рисунок 1.10. Экранная форма задачи (1.1)–(1,2) после получения решения Отчет по результатам Отчет по результатам состоит из трех таблиц (рис. 1.14):
Рисунок 1.14. Отчет по результатам 1) таблица 1 содержит информацию о ЦФ; 2) таблица 2 содержит информацию о значениях переменных, полученных в результате решения задачи; 3) таблица 3 показывает результаты оптимального решения для ограничений и для граничных условий. Если ресурс используется полностью (то есть ресурс дефицитный), то в графе "Статус" ("Состояние") соответствующее ограничение указывается как "связанное"; при неполном использовании ресурса (то есть ресурс недефицитный) в этой графе указывается "не связан". В графе "Значение" приведены величины использованного ресурса. Для граничных условий в графе "Разница" показана разность между значением переменной в найденном оптимальном решении и заданным для нее граничным условием. Таблица 3 отчета по результатам дает информацию для анализа возможного изменения запасов недефицитных ресурсов при сохранении полученного оптимального значения ЦФ. Так, если на ресурс наложено ограничение типа ≥, то в графе "Разница" дается количество ресурса, на которое была превышена минимально необходимая норма. Если на ресурс наложено ограничение типа ≤, то в графе "Разница" дается количество ресурса, которое не используется при реализации оптимального решения.
Отчет по устойчивости Отчет по устойчивости состоит из двух таблиц (рис. 1.15).
Рисунок 1.15. Отчет по устойчивости. Таблица 1 содержит информацию, относящуюся к переменным. А. Результат решения задачи. Б. Нормированная стоимость, которая показывает, на сколько изменится значение ЦФ в случае принудительного включения единицы этой продукции в оптимальное решение. Например, в отчете по устойчивости для рассматриваемой задачи (см. рис. 1.15) нормированная стоимость Х3 равна –104,4 руб./шт. Это означает, что если мы, несмотря на оптимальное решение, потребуем включить в план выпуска 1 единицу Х3, то новый план выпуска принесет нам прибыль на 104,4 руб. меньше, чем в прежнем оптимальном решении. В. Коэффициенты ЦФ. Г. Предельные значения приращения целевых коэффициентов ∆сi, при которых сохраняется первоначальное оптимальное решение. Например, допустимое уменьшение цены на Х1 равно 114,6 руб./шт., а допустимое увеличение – практически не ограничено. Это задает соотношение устойчивости для коэффициентов целевой функции. Примечание. При выходе за указанные в отчете по устойчивости пределы изменения цен оптимальное решение может меняться как по номенклатуре выпускаемой продукции, так и по объемам выпуска (без изменения номенклатуры). Таблица 2 (см. рис. 1.15) содержит информацию, относящуюся к ограничениям. А. Величина использованных ресурсов в колонке "Результ. значение". Б. Предельные значения приращения ресурсов ∆bj. В графе "Допустимое Уменьшение" показывают, на сколько можно уменьшить (устранить излишек) или увеличить ресурс, сохранив при этом оптимальное решение. Для ограничений, не позволяющих выпускать большее, чем в оптимальном решении, количество продукции и получать более высокую прибыль возникает вопрос, на сколько максимально может возрасти это ограничение, чтобы обеспечить увеличение выпуска продукции. Ответ на этот вопрос показан в графе "Допустимое Увеличение". Это приведет к новым оптимальным решениям, увеличивающим прибыль. Дальнейшее увеличение таких ограничений сверх указанных пределов не будет больше улучшать решение, т.к. уже другие ресурсы станут связывающими. В. Объективно-обусловленная оценка j-го ресурса (теневая цена) рассчитывается только для существенных (дефицитных) ресурсов. Объективно-обусловленная оценка j-го ресурса показывает, насколько увеличится целевая функция при увеличении j-го ресурса на единицу. Задания для самостоятельной работы Задание 1.1. Для откорма животных используется три вида комбикорма: А, В и С. Каждому животному в сутки требуется не менее 800 г. жиров, 700 г. белков и 900 г. углеводов. Содержание в 1 кг. каждого вида комбикорма жиров белков и углеводов (граммы) приведено в таблице:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 395; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.85.76 (0.118 с.) |
Привить студентам навыки применения методологии экономико-математического моделирования и инструментальных методов экономики в решении практических задач управления бизнесом.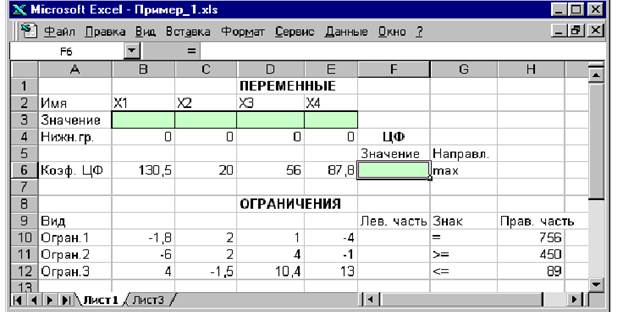
Рисунок 1.1. Экранная форма задачи (1.1)–(1,2) (курсор в ячейке F6)
(для версии 2010 кнопку Файл), а затем щелкните Параметры Excel. Выберите команду Надстройки и в окне Управление выберите пункт Надстройки Excel. Нажмите кнопку Перейти. В окне Доступные надстройки установите флажок Поиск решения, а затем нажмите кнопку ОК. Совет: если Поиск решения отсутствует в списке поля Доступные надстройки, то для проведения поиска нажмите кнопку Обзор.
