
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вариациям коэффициентов целевой функции.Содержание книги
Поиск на нашем сайте
    
      Вариации коэффициентов целевой функции ЗЛП приводят к изменению направления вектора градиента. Так как при этом не затрагивается допустимое множество, то прежнее решение остается допустимым базисным, а оптимальное решение может измениться. Вариации коэффициентов целевой функции ЗЛП приводят к изменению направления вектора градиента. Так как при этом не затрагивается допустимое множество, то прежнее решение остается допустимым базисным, а оптимальное решение может измениться.
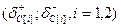 , которые находятся из условия возможности изменения направления , которые находятся из условия возможности изменения направления 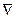 Z внутри конуса, определяемого векторами-градиентами активных ограничений 2 и 3. Z внутри конуса, определяемого векторами-градиентами активных ограничений 2 и 3.
Формальный анализ чувствительности оптимального решения к вариациям коэффициентов целевой функции может быть произведен с использованием заключительной симплекс-таблицы
Рис. 3.2 Структура симплекс-таблицы Вариации коэффициентов целевой функции приводят к изменению симплекс-разностей
(3.1) где
Анализ этой формулы позволяет выделить два случая: - варьируется - варьируется где В первом случае
К изменению оптимального решения при этом может привести лишь положительная вариация
Предельные отрицательные вариации по коэффициентам целевой функции небазисных переменных равны:
Рассмотрим второй случай Пусть
Очевидно, что при вариациях такого
При этом увеличиваться симплекс-разности будут в следующих случаях: - при положительных вариациях - при отрицательных вариациях В соответствий с этими рассуждениями формулы для определения предельных вариаций коэффициентов целевой функции для случая
(3.7)
Где (3.9) Если произведена вариация - скорректировать строку симплекс-разностей
где - применить к скорректированной симплекс-таблице алгоритм поиска оптимального решения, В результате его работы либо будет найдено новое оптимальное решение, либо установлено, что целевая функция при данной вариации неограничена на допустимом множестве. Последнее реализуется в том случае, если допустимое множество имеет образующие, и градиент целевой функции изменял свое направление таким образом, что стал образовывать острый угол с направляющим векторов хотя бы одной из них.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 169; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.141.142 (0.01 с.) |

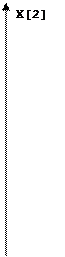
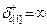
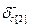
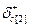
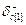
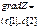
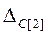 При положительной вариации больше предельной оптимальное решение переместится в крайнюю точку(КТ) 3, а при отрицательной - в КТ 5.
При положительной вариации больше предельной оптимальное решение переместится в крайнюю точку(КТ) 3, а при отрицательной - в КТ 5. 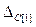 Отрицательная вариация больше предельной (
Отрицательная вариация больше предельной ( 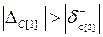 ) приведет к перемещению оптимального решения либо в КТ 3, либо в КТ 2.
) приведет к перемещению оптимального решения либо в КТ 3, либо в КТ 2.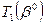 . Структура симплекс-таблицы
. Структура симплекс-таблицы 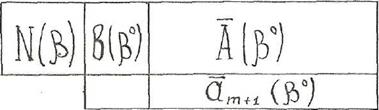
 . В заключительной симплекс-таблице
. В заключительной симплекс-таблице 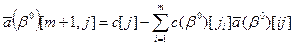 Формула расчета симплекс-разности для каждого j-го столбца симплекс-таблицы имеет следующий вид:
Формула расчета симплекс-разности для каждого j-го столбца симплекс-таблицы имеет следующий вид: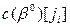 -коэффициенты целевой функции при базисных переменных;
-коэффициенты целевой функции при базисных переменных;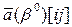 -коэффициенты матрицы
-коэффициенты матрицы 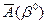 , являющейся составной частью симплекс-таблицы
, являющейся составной частью симплекс-таблицы 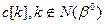 ;
;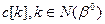 ,
,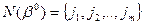 - базисное множество, соответствующее оптимальному решению
- базисное множество, соответствующее оптимальному решению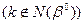 будет меняться лишь симплекс-разность k-о столбца
будет меняться лишь симплекс-разность k-о столбца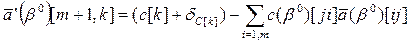 (3.2)
(3.2)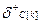 , которую можно определить, приравняв соотношение (3.2) к нулю:
, которую можно определить, приравняв соотношение (3.2) к нулю: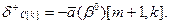 (3.3)
(3.3)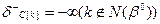 (3.4)
(3.4)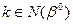
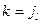 . Тогда:
. Тогда: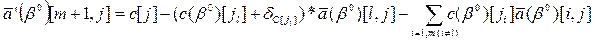 (3.5)
(3.5)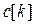 будет изменяться не одна симплекс-разность, а все те из них, которым в l-ой строке матрицы
будет изменяться не одна симплекс-разность, а все те из них, которым в l-ой строке матрицы 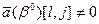 (3.6)
(3.6)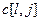 , если
, если 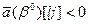 ;
;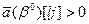
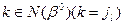 имеют вид:
имеют вид: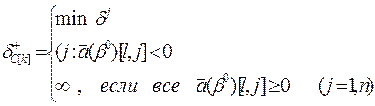
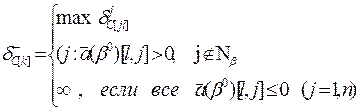 (3.8)
(3.8)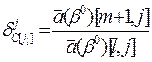
 больше предельной, то, чтобы найти новое решение ЗЛП, необходимо:
больше предельной, то, чтобы найти новое решение ЗЛП, необходимо: (для базиса
(для базиса  ), ставшего теперь уже неоптимальным
), ставшего теперь уже неоптимальным  , а в случае
, а в случае  и величину
и величину  определяющую значение целевой функции:
определяющую значение целевой функции:

 рассчитываются с учетом проведенной вариации;
рассчитываются с учетом проведенной вариации;


