
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближённые методы решения СЛАУСодержание книги
Поиск на нашем сайте
Лекция 1 Приближённые методы решения СЛАУ А) Метод простых итераций. (Метод последовательных приближений). Пусть дана система n линейных уравнений с n неизвестными:
или Задаются произвольно n-чисел – нулевое приближение искомой функции.
Далее подставляем в правую часть системы (1) нулевое приближение и находим первое приближение.
Затем по 1-ому приближению находят 2-ое, 3-е и т.д. В результате для k-ого приближения получаем формулу:
Таким образом мы получили последовательность векторов Х(0),Х(1),…, Х(К), к=1,2,… Если любая из таких последовательностей {Хi(к)} сходится некоторому пределу В равенстве (2’) перейдем к пределу при k→∞ при замене хi на сi.
Теорема (достаточные условия сходимости простой итерации): Пусть выполняется хотя бы одно из следующих условий (нормы матрицы): а) Если максимум суммы модулей коэффициентов при неизвестных (по строкам) меньше 1: б) Если максимум суммы модулей коэффициентов при неизвестных (по столбцам) меньше 1: в) Если сумма всех элементов в квадрате меньше 1.
Если выполняется хотя бы одно, тогда справедливы утверждения: 1) система (1) имеет единственное решение (С1,... Сn); 2) последовательность 3) для приближенного равенства верны оценки (x1(k),…xn(k)) а’) есливыполняется условие а), то
б’) если выполняется условие б), то
в’) если выполняется условие в), то
Замечания: 1)Если нет никакой информации о точном решении СЛАУ, то за начальное приближение выбираем столбец свободных коэффициентов. 2)остановка вычислений производной по заданной величине абсолютной погрешности Б) Метод Зейделя. Этот метод является модификацией МПИ и заключается в том, что при вычислении (к+1) приближения неизвестного хi (i>1), используются уже вычисленные ранее (к+1) приближения неизвестных х1, х2,…, хi-1 Рассмотрим систему: Пусть матрица α удовлетворяет одному из условий теоремы: Если, а) б)
в)
тогда общая формула метода Зейделя имеет вид:
к=1,2…
Замечание: метод Зейделя обычно, но не всегда сходится к точному решения быстрее, чем МПИ
В) Метод Гаусса. (Метод последовательного исключения переменных) Матрица называется верхнетреугольной, если ниже главной диагонали все элементы равны нулю, т.е. aij=0 при i>j. Аналогично, матрица называется нижнетреугольной, если все элементы выше главной диагонали (i<j) равны 0. Матрица называется диагональной, если только на главной диагонали (i=j) стоят ненулевые элементы. Метод Гаусса решения систем линейных уравнений состоит из двух этапов: прямого хода и обратного хода.
Прямой ход. Это основной этап решения системы уравнений с помощью метода Гаусса. Его суть состоит в приведении исходной расширенной матрицы системы к верхнетреугольной матрице с помощью эквивалентных преобразований (добавление к строке любой линейной комбинации других строк и перестановка строк, т.е. уравнений). Формулы прямого хода соответствуют последовательному выражению переменных из уравнений и подстановке их в последующие уравнения, т.е. их фактическому исключению из последующих уравнений системы. При этом шагом считается исключение одной переменной из всех последующих уравнений системы. Рассмотрим k-ый шаг прямого хода. На k-ом шаге матрица системы имеет вид: (а11 а12 … а1k … a1n | b1) (0 a22 … a2k … a2n | b2) (0 … … … … …) (0 0 … akk … akn | bk) (0 … … … … …) (0 0 … ank … ann | bn) Осталось n-k+1 неизвестных. Чтобы удалить х(k) из последней строчки, например, надо из нее вычесть k-ую строчку с таким коэффициентом, чтобы получить на месте аnk ноль. Для этого коэффициент должен быть равен cnk=ank/akk. Элемент аkk называется разрешающим элементом k-ого шага и должен быть отличен от 0. Формулы прямого хода
cmk=amk/akk где 1<= k<n bm=bm-cmkbk, k<m<=n aml=aml-cmkakl, k<=l<=n
Обратный ход
Последовательное вычисление значения неизвестных xn, xn-1,..., х1 (именно в таком порядке) для полученной после прямого хода верхнетреугольной системы называется обратным ходом.
Формулы обратного хода.
для k=n,n-1,…,1.
Лекция 2. Выбор шага
1. Пусть требуется вычислить интеграл с точностью ε. Используя формулу соответствующего остаточного члена R, выбирают h таким образом, чтобы выполнялось неравенство
2. Двойной пересчёт. (Правило Рунге).
Лекция 4 ЧИСЛЕННОЕ РЕШЕНИЕ ТРАНСЦЕНДЕНТНЫХ И НЕЛИНЕЙНЫХ УРАВНЕНИЙ.
Если алгебраическое или трансцендентное уравнение достаточно сложное, то его корни сравнительно редко удаётся найти точно. Поэтому большое значение приобретают способы приближённого нахождения корней уравнения и оценки степени их точности. Процесс нахождения приближённых значений корней уравнения: f(x) = 0, (1) где функция f(x) определена и непрерывна в некотором конечном или бесконечном интервале a < x < b разбивается на два этапа: 1) отделение корней; 2) уточнение корней до заданной степени точности.
Отделение корней.
Всякое значение λ, обращающее функцию f(x) в нуль, т. е. такое, что f(λ) = 0, называется корнем уравнения (1) или нулём функции f(x). Отделить корни − это значит разбить всю область допустимых значений на отрезки, в каждом из которых содержится один корень. Отделение корней можно произвести двумя способами − графическим и аналитическим.
Графический метод отделения корней: a) строят график функции у = f(x) для уравнения вида f(x) = 0. Значения действительных корней уравнения являются абсциссы точек пересечения графика функции у = f(x) с осью Ох (рис.1); b) представляют уравнение (1) в виде φ(х) = g(x) и строят графики функций у = φ(х) и у = g(x). Значения действительных корней уравнения являются абсциссы точек пересечения графиков функций у = φ(х) и у = g(x) (рис.2). Отрезки, в которых заключено только по одному корню, легко находятся.
Рис.1. Рис.2.
если непрерывная на отрезке производная
Рис.3
Вычисляем После каждой итерации отрезок, на котором расположен корень уменьшается вдвое, то есть после n итераций он сокращается в 2n раз. Таким образом, число итераций n в данном методе зависит от предварительно заданной точности ε и от длины исходного отрезка и не зависит от вида функции f(x). Это является важным преимуществом метода половинного деления по сравнению с другими методами. Метод, однако, медленно сходится при задании высокой точности расчёта.
Метод хорд. Пусть на отрезке [a,b] функция f(x) непрерывна и принимает на концах отрезка значения разных знаков, а производные f ′(x) и f ″(x) сохраняют постоянный знак на интервале (a,b). Тогда возможны четыре случая расположения дуги кривой (рис.4).
В методе хорд за очередное приближение берём точку пересечения с осью Х прямой (рис.5), соединяющей точки (a,f(a)) и (b,f(b)) Причём одна из этих точек фиксируется − та, для которой знаки f(x) и f ″(x) одинаковы. Для рис.5 неподвижным концом хорды является х =a. Уравнение хорды АВ: Точка пересечения хорды с осью Х (у=0):
Теперь корень находится на отрезке [a,c1]. Заменяем b на с1.
Рис.5. Иллюстрация метода хорд.
Применяя метод хорд к этому отрезку, получим:
Продолжим и т.д., получим: │сn+1 − cn│< ε или │f(cn)│< ε1. Для оценки погрешности можно пользоваться общей формулой:
Итак, если f (x)∙f″(x) > 0, то приближённое значение корня находят по формуле (2), если f(x)∙f″(x) < 0 (т.е. фиксируется х = b), то по формуле:
Лекция 5. Приближённое решение обыкновенных дифференциальных уравнений и систем обыкновенных дифференциальных уравнений. Пусть функция у = f(x,y) отражает количественную сторону некоторого явления. Рассматривая это явление, мы можем установить характер зависимости между величинами х и у, а также производными от у по х, т.е. написать дифференциальное уравнение. Определение: Обыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную х, искомую функцию y=f(x) и её производные. Запись: F(x, y, y′, y′′,…, y(n)) = 0 или Определение: Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. у′-2ху3+5=0----- уравнение первого порядка, у″+ky′-by-sinx=0------ уравнение второго порядка. Задача Коши (для уравнения первого порядка): у′ = f(x, y) (1) найти решение y = y(x), удовлетворяющее начальному условию: у(х0)=у0. (1*). Т.е. найти интегральную кривую, проходящую через точку М(х0, у0). Если f(x,y) непрерывна в области R: |x-x0| < a, |y-y0| < b, то существует по меньшей мере одно решение у = у(х), определённое в некоторой окрестности: |х-х0| < h, где h ― положительное число. Это решение единственно, если в R выполнено условие Липшица: Где N― постоянная (константа Липшица), зависящая в общем случае от a и b. Если f(x,y) имеет ограниченную производную Для дифференциального уравнения n-го порядка: у(n)=f(x,y,y′,…,y(n-1)) задача Коши состоит в нахождении решения у = у(х), удовлетворяющего начальным условиям: у(х0) = у0, у′(х0) = у′0, …, у(n-1)(x0) = y(n-1)0 ― заданные числа. Функция у = f(x, C1, C2,…, Cn), где С1,…, Сn― произвольные постоянные, называется общим решением ОДУ или общим интегралом. Эти постоянные можно определить с помощью начальных условий. Решение ДУ при заданных начальных условиях называется его частным решением. Определение: задача называется краевой, если указывается интервал интегрирования [a,b] и ставятся дополнительные условия для значений функции у и её производных на концах этого интервала.
Процесс познания закономерностей и стремление создать детальную картину исследуемых явлений приводит к более сложной количественной оценке, отражающей эти явления, а именно к функции многих переменных, зависящих как от пространственных координат, так и от времени u = f(x1, x2,…, xn, t).
Определение: Дифференциальным уравнением с частными производными называется уравнение, связывающее независимую переменные х1, х2, …, хn, t, искомую функцию u = f (х1, х2, …, хn, t) и её частные производные:
Постановка задачи. Дано дифференциальное уравнение первого порядка: у′ = f(x,y) (1). Требуется найти решение этого уравнения на отрезке [x0, xmax], удовлетворяющее начальным условиям: у(х0) = у0 (2). В вычислительной практике более предпочтительным являются численные методы нахождения приближённого решения в фиксированных точках: х0<x1<…<xn=xmax. Большинство численных методов решения задачи (1) с начальными условиями (2) можно привести к виду:
― при r = 1, а1 = 1, b0 = 0 методы вида (3) называются одношаговыми (чтобы найти yi+1 требуется информация только о предыдущей точке (xi, yi)). ― при r > 1 и b0 = 0 ― явными многошаговыми. ― при r > 1 и b0 ≠ 0 ― неявными многошаговыми. Многошаговость нарушает однородность вычислительного процесса, используя для получения недостающей информации другие вычислительные схемы (например, одношаговые). А) Метод Эйлера.
Для решение Д.У.(1) с Н.У. (2) на отрезке [x0, xmax] по методу Эйлера, таблица приближённых значений у(х) для равноотстоящих узлов:
строится по формулам: yk+1 = yk + h∙f(xk,yk) xk+1 = xk + h, k = 0,…,n-1, h=(xn-x0)/n (4)
Абсолютная погрешность формулы (4) на каждом шаге имеет порядок h2
Формула (4) означает, что на отрезке [xk, xk+1] интегральная кривая y = y(x) приближённо заменяется прямолинейным отрезком, выходящим из точки М(хk;уk) с угловым коэффициентом f(хk;уk). В качестве приближения искомой интегральной кривой получаем ломаную линию с вершинами в точках М0(х0;у0), М1(х1;у1),…, Мn(хn;уn). Первое звено касается истинной интегральной кривой в точке М0(х0;у0).
Метод Эйлера может быть применён к решению системы ОДУ и ДУ высших порядков. Последние должны быть предварительно приведены к системе ОДУ первого порядка. Пусть задана система ОДУ первого порядка: с начальными условиями: у(х0) = у0, z(х0) = z0 (7)
Приближённые значения у(хi) ≈ yi, z(хi) ≈ zi вычисляются по формулам:
Метод Эйлера обладает двумя существенными недостатками: 1) малой точностью (метод первого порядка точности); 2) систематическое накопление ошибок. В) Модификации метода Эйлера. 1ый усовершенствованный метод Эйлера.
Сначала вычисляют промежуточные значения:
А затем полагают:
2oй усовершенствованный метод Эйлера.
Сначала определяют «грубые приближения»:
И приближённо полагают:
Локальная погрешность на i-ом шаге:
С.) Метод Рунге-Кутта. (4го порядка)
Наиболее знаменитым из методов Рунге-Кутта является классический метод 4го порядка
Грубая оценка погрешности (двойной просчёт): Где у(хi) – точное решение, у*i – приближённое решение с шагом h/2, yi – … с шагом h. Для оценки правильности выбора шага h используют равенство:
q должно равняться нескольким сотым, иначе h уменьшается. Многошаговые методы. ( используют информацию о нескольких предыдущих точках) Д ) Алгоритм Адамса.
Пусть дано дифференциальное уравнение: у′ = f(x, y) (1) с начальными условиями: у(х0) = у0 (1*) Требуется найти решение уравнения (1) на отрезке [a,b]. Разобьём отрезок [a,b] на n равных частей точками хi = х0 + ih (i =0, 1, …, n). 1ый этап: стартовая процедура. Используют какой-либо одношаговый метод того же порядка точности до тех пор, пока не будет получено достаточно значений для работы многошагового метода. Следовательно, определены: у1, у2, …, уk-1 в точках: х0 + h, …, x0 + h(k-1). 2ойэтап: рекурсивной процедуры. Определение: уk, yk+1,…, yn основано на интегрировании интерполяционного многочлена Ньютона. Рабочие формулы явных методов Адамса (2-го, 3-го, 4-го порядков).
Формулы (2)-(4) называются экстраполяционными и на практике используются в качестве прогноза.
Для улучшения точности или коррекции результата применяют неявные методы (используют ещё ненайденные значения: уk+1, yk+2,…).
Формулы (5)-(7) называются интерполяционными. Для грубой оценки точности (двойной просчёт):
Лекция 1 Приближённые методы решения СЛАУ А) Метод простых итераций. (Метод последовательных приближений). Пусть дана система n линейных уравнений с n неизвестными:
или Задаются произвольно n-чисел – нулевое приближение искомой функции.
Далее подставляем в правую часть системы (1) нулевое приближение и находим первое приближение.
Затем по 1-ому приближению находят 2-ое, 3-е и т.д. В результате для k-ого приближения получаем формулу:
Таким образом мы получили последовательность векторов Х(0),Х(1),…, Х(К), к=1,2,… Если любая из таких последовательностей {Хi(к)} сходится некоторому пределу В равенстве (2’) перейдем к пределу при k→∞ при замене хi на сi.
Теорема (достаточные условия сходимости простой итерации): Пусть выполняется хотя бы одно из следующих условий (нормы матрицы): а) Если максимум суммы модулей коэффициентов при неизвестных (по строкам) меньше 1: б) Если максимум суммы модулей коэффициентов при неизвестных (по столбцам) меньше 1: в) Если сумма всех элементов в квадрате меньше 1.
Если выполняется хотя бы одно, тогда справедливы утверждения: 1) система (1) имеет единственное решение (С1,... Сn); 2) последовательность 3) для приближенного равенства верны оценки (x1(k),…xn(k)) а’) есливыполняется условие а), то
б’) если выполняется условие б), то
в’) если выполняется условие в), то
Замечания: 1)Если нет никакой информации о точном решении СЛАУ, то за начальное приближение выбираем столбец свободных коэффициентов. 2)остановка вычислений производной по заданной величине абсолютной погрешности Б) Метод Зейделя. Этот метод является модификацией МПИ и заключается в том, что при вычислении (к+1) приближения неизвестного хi (i>1), используются уже вычисленные ранее (к+1) приближения неизвестных х1, х2,…, хi-1 Рассмотрим систему: Пусть матрица α удовлетворяет одному из условий теоремы: Если, а) б) в)
тогда общая формула метода Зейделя имеет вид:
к=1,2…
Замечание: метод Зейделя обычно, но не всегда сходится к точному решения быстрее, чем МПИ
В) Метод Гаусса. (Метод последовательного исключения переменных) Матрица называется верхнетреугольной, если ниже главной диагонали все элементы равны нулю, т.е. aij=0 при i>j. Аналогично, матрица называется нижнетреугольной, если все элементы выше главной диагонали (i<j) равны 0. Матрица называется диагональной, если только на главной диагонали (i=j) стоят ненулевые элементы. Метод Гаусса решения систем линейных уравнений состоит из двух этапов: прямого хода и обратного хода.
Прямой ход. Это основной этап решения системы уравнений с помощью метода Гаусса. Его суть состоит в приведении исходной расширенной матрицы системы к верхнетреугольной матрице с помощью эквивалентных преобразований (добавление к строке любой линейной комбинации других строк и перестановка строк, т.е. уравнений). Формулы прямого хода соответствуют последовательному выражению переменных из уравнений и подстановке их в последующие уравнения, т.е. их фактическому исключению из последующих уравнений системы. При этом шагом считается исключение одной переменной из всех последующих уравнений системы. Рассмотрим k-ый шаг прямого хода. На k-ом шаге матрица системы имеет вид: (а11 а12 … а1k … a1n | b1) (0 a22 … a2k … a2n | b2) (0 … … … … …) (0 0 … akk … akn | bk) (0 … … … … …) (0 0 … ank … ann | bn) Осталось n-k+1 неизвестных. Чтобы удалить х(k) из последней строчки, например, надо из нее вычесть k-ую строчку с таким коэффициентом, чтобы получить на месте аnk ноль. Для этого коэффициент должен быть равен cnk=ank/akk. Элемент аkk называется разрешающим элементом k-ого шага и должен быть отличен от 0. Формулы прямого хода
cmk=amk/akk где 1<= k<n bm=bm-cmkbk, k<m<=n aml=aml-cmkakl, k<=l<=n
Обратный ход
Последовательное вычисление значения неизвестных xn, xn-1,..., х1 (именно в таком порядке) для полученной после прямого хода верхнетреугольной системы называется обратным ходом.
Формулы обратного хода.
для k=n,n-1,…,1.
Лекция 2.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 210; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.21.141 (0.013 с.) |


 (1)
(1) где
где 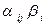 - заданные числа;
- заданные числа; 
 .
.
 ,
,  (2)
(2) ,
,  (2’)
(2’) xik = ci,
xik = ci, 



 , где i =
, где i =  определяется по формуле (2), при любом начальном приближении
определяется по формуле (2), при любом начальном приближении  сходится к соответствующим компонентам точного решения.
сходится к соответствующим компонентам точного решения.  i =
i = 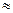 (C1,…Cn),
(C1,…Cn), ,
, ,
, .
.
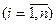 (из приведенной матрицы);
(из приведенной матрицы);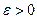 и приведенным в теореме оценкам.
и приведенным в теореме оценкам. i=1,n
i=1,n <1 (коэффициенты по строкам)
<1 (коэффициенты по строкам) <1 (коэффициенты по столбцам)
<1 (коэффициенты по столбцам) <1 (все коэффициенты)
<1 (все коэффициенты)
 ,откуда получаем:
,откуда получаем: 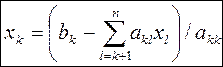
 .
.

 Аналитический метод отделения корней основан на следующей теореме:
Аналитический метод отделения корней основан на следующей теореме: функция
функция  принимает на концах отрезка значения разных знаков, т.е.
принимает на концах отрезка значения разных знаков, т.е.  , то внутри этого отрезка находится хотя бы один корень уравнения
, то внутри этого отрезка находится хотя бы один корень уравнения  ; если при этом
; если при этом сохраняет знак внутри отрезка
сохраняет знак внутри отрезка  , выбираем отрезок
, выбираем отрезок  и т.д. Как только будет выполнено
и т.д. Как только будет выполнено  , то в качестве приближенного значения корня, вычисленного с точностью
, то в качестве приближенного значения корня, вычисленного с точностью 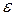 , можно взять
, можно взять  .
.




 .
.
 .
.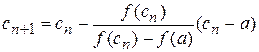 (2) Условие окончания вычислений:
(2) Условие окончания вычислений: , где
, где 
 . (3)
. (3) .
.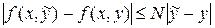 (2)
(2) в R, то можно положить:
в R, то можно положить: 
 .
. (3).
(3). (5)
(5) (6)
(6) (8)
(8) (9)
(9) (10)
(10) (11)
(11) (12)
(12) . Оценка погрешности в точке хn может быть получена с помощью двойного просчёта (с шагом h и h/2):
. Оценка погрешности в точке хn может быть получена с помощью двойного просчёта (с шагом h и h/2): (13)
(13)
 (14)
(14)
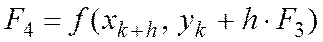
 (15)
(15) (16)
(16) (17)
(17) (2)
(2) (3)
(3) (4)
(4) (5)
(5) (6)
(6) (7)
(7)



