
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Ньютона (касательных).Содержание книги
Поиск на нашем сайте
Пусть на отрезке [a,b] функция f(x) непрерывна и принимает на концах отрезка значения разных знаков, а производные f ′(x) и f ″(x) сохраняют постоянный знак на интервале (a,b). Геометрический смысл метода касательных состоит в том, что дуга кривой y = f(x) заменяется касательной к этой кривой.
Рис.7. Иллюстрация метода касательных.
Выберем в качестве начального приближения х0 = a и проведём в точке А0(a,f(a)) касательную к графику функции f(x). Абсцисса пересечения касательной с осью Ох (у = 0) является первым приближением к корню (рси.7):
Через точку А1(х1;f(x1)) снова проведём касательную, абсцисса точки пересечения которой даст второе приближение х2 корня ξ и т.д. Очевидно, что в точке Аn(xn;f(xn)): y − f(xn) = f ′(xn)(x−xn) и алгоритм метода Ньютона запишется так:
Заметим, что в нашем случае, если положить х0 = b и провести касательную к кривой у = f(x) в точке b, то первое приближение не принадлежит отрезку [a,b].
Таким образом, в качестве начального приближения х0 выбирается тот конец интервала [a,b], для которого знаки f(x) и f ″(x) одинаковы.
Условие окончания вычислений:
│сn+1 − cn│< ε или │f(cn)│< ε1.
Для оценки погрешности можно пользоваться общей формулой
Комбинированный метод (хорд и касательных). Методы хорд и касательных дают приближения корня с разных сторон. Поэтому их часто применяют в сочетании друг с другом, и уточнение корня происходит быстрее. Пусть дано уравнение f(x)=0, корень ξ отделён и находится на отрезке [a,b]. Применим комбинированный метод хорд и касательных с учётом типа графика функции (рис.4). Если f (x)·f ″(x) < 0 (рис.4 в, г), то методом хорд получаем значение корня с избытком, а методом касательных – с недостатком. Если f (x)·f ″(x) > 0 (рис.4 а, б), то метод хорд даёт приближение корня с недостатком, а метод касательных – с избытком. Рассмотрим случай, когда f (b) < 0, f ″(x) > 0 (рис.8), то со стороны конца а лежат приближённые значения корня, полученные по методу касательных, а со стороны конца b – значения, полученные по методу хорд.
Рис.8 Иллюстрация комбинированного метода. Тогда Теперь истинный корень ξ находится на интервале [a1,b1]. Применяя к этому интервалу комбинированный метод, получаем
и вообще
Для случая, когда f (b)·f ″(x) > 0, то рассуждая аналогично, получим следующие формулы для уточнения корня уравнения:
Комбинированный метод очень удобен при оценке погрешности вычислений. Процесс вычислений прекращается, как только станет выполняться неравенство |bn+1–an+1| < ε. Корень уравнения есть среднее арифметическое последних полученных значений: ξ=(an+1+bn+1)/2 Лекция 5. Приближённое решение обыкновенных дифференциальных уравнений и систем обыкновенных дифференциальных уравнений. Пусть функция у = f(x,y) отражает количественную сторону некоторого явления. Рассматривая это явление, мы можем установить характер зависимости между величинами х и у, а также производными от у по х, т.е. написать дифференциальное уравнение. Определение: Обыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную х, искомую функцию y=f(x) и её производные. Запись: F(x, y, y′, y′′,…, y(n)) = 0 или Определение: Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. у′-2ху3+5=0----- уравнение первого порядка, у″+ky′-by-sinx=0------ уравнение второго порядка. Задача Коши (для уравнения первого порядка): у′ = f(x, y) (1) найти решение y = y(x), удовлетворяющее начальному условию: у(х0)=у0. (1*). Т.е. найти интегральную кривую, проходящую через точку М(х0, у0). Если f(x,y) непрерывна в области R: |x-x0| < a, |y-y0| < b, то существует по меньшей мере одно решение у = у(х), определённое в некоторой окрестности: |х-х0| < h, где h ― положительное число. Это решение единственно, если в R выполнено условие Липшица: Где N― постоянная (константа Липшица), зависящая в общем случае от a и b. Если f(x,y) имеет ограниченную производную Для дифференциального уравнения n-го порядка: у(n)=f(x,y,y′,…,y(n-1)) задача Коши состоит в нахождении решения у = у(х), удовлетворяющего начальным условиям: у(х0) = у0, у′(х0) = у′0, …, у(n-1)(x0) = y(n-1)0 ― заданные числа. Функция у = f(x, C1, C2,…, Cn), где С1,…, Сn― произвольные постоянные, называется общим решением ОДУ или общим интегралом. Эти постоянные можно определить с помощью начальных условий. Решение ДУ при заданных начальных условиях называется его частным решением.
Определение: задача называется краевой, если указывается интервал интегрирования [a,b] и ставятся дополнительные условия для значений функции у и её производных на концах этого интервала.
Процесс познания закономерностей и стремление создать детальную картину исследуемых явлений приводит к более сложной количественной оценке, отражающей эти явления, а именно к функции многих переменных, зависящих как от пространственных координат, так и от времени u = f(x1, x2,…, xn, t). Определение: Дифференциальным уравнением с частными производными называется уравнение, связывающее независимую переменные х1, х2, …, хn, t, искомую функцию u = f (х1, х2, …, хn, t) и её частные производные:
Постановка задачи. Дано дифференциальное уравнение первого порядка: у′ = f(x,y) (1). Требуется найти решение этого уравнения на отрезке [x0, xmax], удовлетворяющее начальным условиям: у(х0) = у0 (2). В вычислительной практике более предпочтительным являются численные методы нахождения приближённого решения в фиксированных точках: х0<x1<…<xn=xmax. Большинство численных методов решения задачи (1) с начальными условиями (2) можно привести к виду:
― при r = 1, а1 = 1, b0 = 0 методы вида (3) называются одношаговыми (чтобы найти yi+1 требуется информация только о предыдущей точке (xi, yi)). ― при r > 1 и b0 = 0 ― явными многошаговыми. ― при r > 1 и b0 ≠ 0 ― неявными многошаговыми. Многошаговость нарушает однородность вычислительного процесса, используя для получения недостающей информации другие вычислительные схемы (например, одношаговые). А) Метод Эйлера.
Для решение Д.У.(1) с Н.У. (2) на отрезке [x0, xmax] по методу Эйлера, таблица приближённых значений у(х) для равноотстоящих узлов:
строится по формулам: yk+1 = yk + h∙f(xk,yk) xk+1 = xk + h, k = 0,…,n-1, h=(xn-x0)/n (4)
Абсолютная погрешность формулы (4) на каждом шаге имеет порядок h2
Формула (4) означает, что на отрезке [xk, xk+1] интегральная кривая y = y(x) приближённо заменяется прямолинейным отрезком, выходящим из точки М(хk;уk) с угловым коэффициентом f(хk;уk). В качестве приближения искомой интегральной кривой получаем ломаную линию с вершинами в точках М0(х0;у0), М1(х1;у1),…, Мn(хn;уn). Первое звено касается истинной интегральной кривой в точке М0(х0;у0).
Метод Эйлера может быть применён к решению системы ОДУ и ДУ высших порядков. Последние должны быть предварительно приведены к системе ОДУ первого порядка. Пусть задана система ОДУ первого порядка: с начальными условиями: у(х0) = у0, z(х0) = z0 (7)
Приближённые значения у(хi) ≈ yi, z(хi) ≈ zi вычисляются по формулам:
Метод Эйлера обладает двумя существенными недостатками: 1) малой точностью (метод первого порядка точности); 2) систематическое накопление ошибок. В) Модификации метода Эйлера. 1ый усовершенствованный метод Эйлера.
Сначала вычисляют промежуточные значения:
А затем полагают:
2oй усовершенствованный метод Эйлера.
Сначала определяют «грубые приближения»:
И приближённо полагают:
Локальная погрешность на i-ом шаге:
С.) Метод Рунге-Кутта. (4го порядка)
Наиболее знаменитым из методов Рунге-Кутта является классический метод 4го порядка
Грубая оценка погрешности (двойной просчёт): Где у(хi) – точное решение, у*i – приближённое решение с шагом h/2, yi – … с шагом h. Для оценки правильности выбора шага h используют равенство:
q должно равняться нескольким сотым, иначе h уменьшается. Многошаговые методы. ( используют информацию о нескольких предыдущих точках) Д ) Алгоритм Адамса.
Пусть дано дифференциальное уравнение: у′ = f(x, y) (1) с начальными условиями: у(х0) = у0 (1*) Требуется найти решение уравнения (1) на отрезке [a,b]. Разобьём отрезок [a,b] на n равных частей точками хi = х0 + ih (i =0, 1, …, n). 1ый этап: стартовая процедура. Используют какой-либо одношаговый метод того же порядка точности до тех пор, пока не будет получено достаточно значений для работы многошагового метода. Следовательно, определены: у1, у2, …, уk-1 в точках: х0 + h, …, x0 + h(k-1). 2ойэтап: рекурсивной процедуры. Определение: уk, yk+1,…, yn основано на интегрировании интерполяционного многочлена Ньютона. Рабочие формулы явных методов Адамса (2-го, 3-го, 4-го порядков).
Формулы (2)-(4) называются экстраполяционными и на практике используются в качестве прогноза.
Для улучшения точности или коррекции результата применяют неявные методы (используют ещё ненайденные значения: уk+1, yk+2,…).
Формулы (5)-(7) называются интерполяционными. Для грубой оценки точности (двойной просчёт):
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 267; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.252.210 (0.009 с.) |


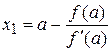 или х0 =
или х0 = 
 .
.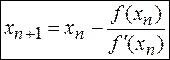 (4)
(4) , где
, где 

 ,
, 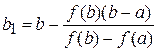 .
. ,
, 
 ,
,  . (5)
. (5) ,
,  . (6)
. (6) .
.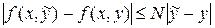 (2)
(2) в R, то можно положить:
в R, то можно положить: 

 .
. (3).
(3). (5)
(5) (6)
(6) (8)
(8) (9)
(9) (10)
(10) (11)
(11) (12)
(12) . Оценка погрешности в точке хn может быть получена с помощью двойного просчёта (с шагом h и h/2):
. Оценка погрешности в точке хn может быть получена с помощью двойного просчёта (с шагом h и h/2): (13)
(13)
 (14)
(14)
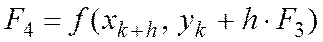
 (15)
(15) (16)
(16) (17)
(17) (2)
(2) (3)
(3) (4)
(4) (5)
(5) (6)
(6) (7)
(7)



