
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулировка теоремы существования и единственности ( ТСЕ ). Понятие общего решения.Содержание книги
Поиск на нашем сайте
Формулировка теоремы существования и единственности (ТСЕ). Понятие общего решения. Обобщение некот понятий. Пусть f(x,y) опред обл DÌR2 X,Y, точка (x0,y0)ÎD. Рассмотрим задачу Коши (8)(y’=f(x,y)(2);y(x0)=y0). Пусть j1(x) и j2(x) решения (8), т.е. j1(x),j2(x)-реш(2) и j1(x0)=y0, j2(x0)=y0. Опред. Говорят, что задача Коши(8) имеет единст решение если любые 2 реш j1(x) и j2(x) этой задачи совпадают на некот окр-сти точки x0 $d>0 "xÎ(x0-d,x0+d):j1(x)ºj2(x) ТСУ1(Локальная) Пусть на обл. DÌR2 X,Y функ.f(x,y) и ее част. производная (¶x/¶y)(x,y) опред. и непрерывны, и точка (x0,y0) ÎD. Тогда урав. y’=f(x,y) имеет решение j(x): 1)опред. на некот. окр-сти (x0-h,x0+h) точки x0, удовл. условию j(x0)=y0; 2)такое решение единственно.(Без док-ва) Замечание к ТСЕ. Пусть в обл D выполн. усл. ТСЕ1. 1)В D беск много решений уравнений. x0-точка(x0,y0)ÎD.Через эту точку проходит реш y=j(x,y0).Все эти решения не совпадают. 2)Решение задачи(8) может быть опред-но лишь на некот окр-сти x0. Пусть f(x,y) удовл в D условиям ТСЕ1. Функцию y=j(x,c) наз-ют общим решения урав(2) в обл D, если: 1)"c:j(x,c)-реш(2); 2)" частное решение урав(2) может быть получено из j(x,c) подбором соотве-его значения c. 2. ОДУ первого порядка, разрешенные относительно производной. Понятия решения и интегральной кривой уравнения. Постановка задачи Коши. Пусть область DÌR2 и f(x,y) определена в D. y’=f(x,y) (1) - ОДУ 1-го порядка разрешенная относительно производной. Опр 1. Функция y=j(x) определена на промежутке I=<a,b> называется решением уравнения (1) если: 1) j(x)ÎC1(I); 2) "xÎI:(x,j(x))ÎD 3)"xÎI: j'(x)=f(x,j(x)). Опр 2. Если y=j(x)- решение (1), то график этой функции называется интегральной кривой уравнения (1). Постановка задачи Коши. Известно: Область DÌR2, f(x,y)-определена в D и точка (x0,y0)ÎD (или числа (x0,y0)ÎD).Надо найти решения y=j(x) уравнения (1) определенное на I, такое что j(x0)=y0 (т.е. интегральная кривая проходящая через (x0,y0)). Числа (x0,y0) называются начальными условиями. Условная запись задачи Коши. Найти решение y’=f(x,y) удовлетворяющее условию y(x0)=y0. Замечания 1) Если функция f(x,y) непрерывна в D то для "(x0,y0)ÎD задача Коши имеет решение в любой точке D. 2) Если f(x,y) непрерывна в D то (1) имеет бесконечно много решений. 3) (x0,y0)ÎD. Для единственности требуется единственное условие. Обобщенное понятие интегральной кривой. D
1) φ(t), ψ(t) 3) Опред2| Если интегральная кривая ур-я (1) задаётся в виде Ф(х,у)=0, то это ур-е будем называть интегралом ур-я (1). Опред3| Уравнение Ф(х,у)=С называется общим интегралом ур-я (1), если1) Ур-е в полных дифференциалах: Пусть P(x,y) и Q(x,y) (2) dU(x,y)= P(x,y)dx+ Q(x,y)dy=0, ясно что dU(x,y)= 0 Замечание. 1) Если существует y* такое что g(y*)=0, то функция y= y*-общее решение уравнения (3). 2) Схема решения (3): а) g(y)=0 находим y*. Функция y= y*-общее решение уравнения (3) б) g(y)¹0. Разделяем переменные dy/g(y)=f(x)dx. Интегрируем òdy/g(y)=òf(x)dx+C. y’=f(ax+by+c) a,bÎR, b¹0 x-независимая переменная. Вводим z(x)=ax+by. zx’=a+byx’ yx’=1/b*(zx-a). Разделяем переменные 1/b*(zx’-a)=f(z) zx’=bf(z)+a-уравнение с разделяющимися переменными. Однородные уравнения. dy/dx=f(x/y) (1) - однородное, x-независимая переменная. u=u(x)=y/x, y=xu, yx’=u+xux’. Подставим в (1) u+xux’=f(u), xux’=f(u)-u, ux’=(f(u)-u)/x. Уравнения сводящиеся к однородному. yx’=f[(a1+b1y+c1)/(a2+b2y+c2)]. a1b2-b1a2¹0 { a1+b1y+c1=0; a2+b2y+c2=0. Пусть решение системы в точке (x0,y0). Разделим переменные {y*=x-x0;y*=y-y0} dy*/dx*=dy/dx, dy*/dx*=f((a1x*+b1y*)/(a2x*+b2y*))-однородная относительно x*, y*. Уравнения Лагранжа и Клеро. Ур-ие Лагранжа: y=f(y’)*x+g(y’) (1); f(y’) ≠y’; y’=p; {x=x(p),y=y(p); {x=x(p),y=f(p)*x+g(p); yx’=f(p)+x*df/dp* px’+dg/dp* px’; p-f(p)=x*df/dp* px’+dg/dp* px’; Если p-f(p) ≠0 и т.к. px’≠0; (p-f(p))* xp’=x*df/dp+dg/dp лин. ур-ие относит. x(p). Если сущ-ет p0 такое, что f(p0)= p0=0, т.е. f(p0)= p0 то ур-ие (1) имеет реш-ие вида; y=f(p0)+g(p0) или y= p0*x+g(p0)); Ур-ие Клеро: y=x*y’+g(y’)(2); вводим параметр p=y’; {x=x(p), y=x*p+g(p); yx’=p+x* px’+ gp’*px’; p = p + x*px’ + gp’*px’; [x + gp’(p)]*px’ = 0; a) px’=0 óp=c; y=c*x+g(c) семейство прямых(реш ур-ия (2)); б) x+g’(p)=0óx=-g’(p); Уравнение интегральной кривой γ: {x = - g’(p); y = - p*g’(p) + g(p); Пусть g(p) ЄC1(I), g’’≠0; в этом случае γ-особая интег-ая кривая(2), пусть p0Є I: (x0;y0) Є γ; { x0 =-g’(p0), y0=- p0g’(p0)+g(p0) Для γ в точке (x0;y0) yx’ - тангенс угла наклона касательной yx’ (x0;y0)= p0; y=c*x+g(c); {x0=-g’(p0), y0=- p0*g’(p0)+g(p0)=c* x0+g(c); yx’(x0)= p0=c; c= p0; реш-ие y= p0*x+g(p0) проходит через точку (x0;y0) касаясь интегр-ой кривой особая инт-ая кривая γ ó γ-особая интегр-ая кривая.
Примеры. (1) F(x, y, y’,..., y (n)) = 0 – называется неразрешённым относительно старшей производной. I. F(x, y ’, y ’’,..., y (n) ) = 0 – функция не содержит y. Осуществим замену переменной: х – независимая переменная; z(x) = y’(x), y’’= z’,…,y(n) = z(n-1) F(x, z, z’, …, z(n-1)) = 0. II. Левая часть не содержит (явно) x. F(y, y’, y’’..., y (n) ) = 0; у – независимая переменная; t = t(y) = yx’; t – функция от у. yxx’’ =(ух’)х’ = tx’= ty’*yx’= t*ty’ yxxx’’’ = (yxx’’)’ = (t*ty’)x’ = (t*ty’)y’*yx’ = t*(t*ty’)y’ F(y, t, ty’..., t (n-1) ) = 0. III. F(x, y, y’,..., y (n)) = 0; Пусть Ф(x, y, y’,..., y (n-1)) такая, что F(x, y, y’,..., y (n)) = d/dxФ(x, y, y’, y’’,..., y (n-1) ), тогда исходное ур. эквивалентно Ф(x, y, y’, y’’,..., y (n-1)) = C. Пример. y*y’’ + y’2 = 1. Решение: (Х)х’ = 1; (y*y’)’ = y*y’’ + y’*y’; (y*y’)x’ = (Х)х’; y*y’ = x + C1; ∫y*dy = ∫(x + C1)dx; y2/2 = x2/2 + C1*x + C2; y2 = x2 + 2*C1*x + 2*C2; K1 = 2*C1; K2 = 2*C2. Ответ: y2 = x2 + K1*x + K2.
Постановка задачи Коши. Пусть x0 Є I, y0, y0’,…, y0 (n-1) - произвольные действ.числа. Найти решение ур. (1), удовлетворяющее начальным условиям: y(x0) = y0, y’(x0) = y0’, …, y(n-1)(x0) = = y0 (n-1). Замечание к ТСЕ 3. Пусть x0 Є I, ур. (2) – однородное, и начальные условия: y(x0) = 0, y’(x0) = 0, …, y(n-1)(x0) = 0. Эта задача Коши имеет только нулевое решение y ≡ 0.
Док-во. Укажем базис в пространстве решений уравнения (7) Зафиксируем точку x0 ∈I y1 (x0)=1, y(1) (x0)=0,…., y(n-1) (x0)=0 По ТСЕ эта задача имеет единственное решение, определенное н а всем промежутке I. Рассмотрим задачу Коши для уравнения (7) с начальными условиями. y(k)(x0)=1, y(i)(x0)=0 I не равно K Эта задача имеет решение.Обозначим его yk+1 (x) Получим систему решений уравнения (7)
Эти решения линейно независимы.
Пусть φ (x)-произвольное решение уравнения (7) Вычислим значение φ (x), φ' (x) ….. в x0∈I Обозначим a1= φ (x0), ,…, an= φ (n-1) (x0) Построим z(x)= a1 y1 (x)+….+ an yn (x)- φ (x) Z(x)-решение уравнения (7) z(x0)= a1 y1 (x0)+….+ an yn (x0)- φ (x0)=0 и все производные тоже равны 0. Итак,решение уравнения (7) z(x) удовлетворяет начальным условиям z(x0)=0,и все остальные производные равны нулю. Следовательно по замечанию к ТСЕ3, решение z(x)=0 z(x)= a1 y1 (x)+….+ an yn (x)- φ (x)=0 y1 (x), ……..,yn(x)-базис в пространстве решений уравнения Замечание ТСЕ 3. Если z(x)= a1 y1 (x)+….+ an yn (x)- φ (x)=0 и y(x0)=0 как и все производные y, то эта задача Коши имеет только нулевое решение y=0.
Действительный случай Пусть a1,..,anÎR (действительные числа). l(t)=t^n+a1t^(n-1)+…+a(n-1)*t+an – многочлен с действительными коэффициентами. Пустьl1, l2,.., ln (li¹lj, i¹j)-корни этого многочлена. а) l1, l2,.., lnÎR, тогда ФСР e^l1x, e^l2x,.., e^lnx – действительная функция y(x)=C1e^l1x+ C2e^l2x+…+ Cn*e^lnx, где С1,..,Сn – произвольные действительные числа
Теорема Пусть lєC, a1, a2,…., am є C; Pm(x) – многочлен степени m с комплексными коэф-ми. l(t)=t^n+a1t^(n-1)+…+a(n-1)t+an – характеристический многочлен уравнения (18.1) и f(x)=Pm(x)e^lx; (19): L[y]=Pm(x)e^lx – неоднородное ЛДУ порядка N. Тогда: 1. (нерезонансный случай). Если l(l)¹0 (т.е. l не является корнем l(t), то уравнение (19) имеет частное решение yч.(x)=Qm(x)e^lx, где Qm(x) – многочлен степени m. 2. (резонансный случай). Если l - корень кратности x многочлена l(t), то уравнение (19) имеет частное решение вида yч.=(x^k)Qm(x)e^lx, где Qm(x) многочлен степени m.
Доказательство (случай m=0, т.е. Pm(x)=A, AÎC; f(x)=Ae^lx) 1. L[y]=Ae^lx; l(l)¹0; yч.=Be^lx (В подлежит определению); Подставляем yч.(x) в (19) L[yч.(x)]=L[Be^lx]=BL[e^lx]=Bl(l)e^lx=f(x)=Ae^lx <=> Bl(l)=A, т.к. l(l)¹0, то B=A/l(l); yч.=A/l(x)e^lx Резонанс. l(l)=0, l - корень кратности k многочленаl(t), т.е. l(t)=(t-l)^k*l1(t), где l1(t)¹0. В этом случае L=l1(p)(p-l)^k. Ищем yч.=Bx^k*e^lx, где В подлежит определению. Уравнение (19) имеет вид L[y]=(l1(p)(p-l)^k)[y]=Ae^lx. Подставим yч. В уравнение: L[Bx^k*e^lx]=B(l1(p)(p-l)^k)[x^k*e^lx]=B(l1(p))[(p-l)^k*(x^k*e^lx))]=B(l1(p))[k(k-1)…1*x^(k-k)e^lx]=Bk!(l1(p)(e^lx))=Bk!*l1(l)*e^lx=Ae^lx, где l1(l)¹0 <=> Bk!*l1(l)=A, B=A/(k!*l1(l) Замечание f(x)=e^ax (Pm(x)cos(bx)+Ql(x)sin(bx)), Pm – многочлен степени m, Ql(x) – многочлен степени l. e^lx=e^(a+ib)x=e^ax*cos(bx)+ e^ax*isin(bx), e^(-lx)=e^(a-ib)x=e^ax*cos(bx)-e^ax*isin(bx) e^ax*cos(bx)=1/2(e^(a+ib)x+ e^(a-ib)x) e^ax*sin(bx)=1/2(e^(a+ib)x-e^(a-ib)x) f(x)=Pm(x)*e^ax*cos(bx)+Ql(x)*e^(a-ib)x =~Ps(x)*e^(a+ib)x+~Qs(x)e^(a-ib)x, где s=max(m,l), Ps(x), Qs(x) – многочлен с комплексными коэффициентами. Лемма Пусть L[y]=f1(x), L[y]=f2(x), L[y]=f1(x)+f2(x). Если j1(x) – решение L[y]=f1(x), j2(x) – решение L[y]=f2(x), то функция j1(x)+j2(x) – решение уравнения L[y]=f1(x)+f2(x) На практике решение ищут в виде: 1. Нерезонансное, т..е. l(a+ib)¹0 yч.н.=e^(ax)*(~Pl(x)*cos(bx)+~Ql(x)*sin(bx)) 2. Резонансное l=(a+ib), l(l)=0 – корень кратности k. yч.н.=x^k*e^(ax)*(~Pl(x)*cos(bx)+~Ql(x)*sin(bx))
Опеределение Нормальной системой ОДУ порядка N называется система вида: {dy1/dx=f1(x,y1,..,yn); dy2/dx=f2(x,y1,..,yn);…; dyn/dx=fn(x,y1,..,yn)} (1) Замечания 1) x – независимая переменная, y1(x),..,yn(x) – функции от x. 2) число уравнений системы (1) равно числу зависимых переменных y1,..,yn 3) порядок системы (1) равен числу уравнений 4) каждое уравнение содержит только одну производную, правосторонних производных нет. Пусть I=<a,b>ÌR Говорят, что на I определены функции y1(x),..,yn(x) и y (x)=(y1(x),..,yn(x))T. Вектор-функция y (x)ÎC1(I) (по определению) <=>(det) "i=1,.,n: yi(x)ÎC1(I) (C(I)) d y /dx=(dy1/dx,..,dyn/dx)T= y ’=(y1`(x),..,yn`(x)) Обозначим fi(x,y1,..,yn)=fi(x, y) Говорят, что WÎRn+1x,y1,..,yn задана вектор-функция f( x. y) =(f1(x, y),.., fn(x, y))T, если на W определены функции f1(x, y),.., fn(x, y) Векторная запись системы (1): d y /dx= f( x. y) (2), y '= f (x, y) Определение Решением системы (1) называется упорядоченный набор функций j1(x),.., jn(x), определенных на I=<a,b> и удовлетворяющих условиям: 1) "i=1,..,n: ji(x)ÎС^1(I) 2) "xÎI: (x, j1(x),.., jn(x))ÎW 3) "i=1,..,n "xÎI: dji(x)/dxºfi(x, j1(x),.., jn(x)) Определение Решением системы (1) называется вектор-функция j(x) =(j1(x),.., jn(x)) T, определенная на промежутке I и удовлетворяющая условиям: j(x) ÎС^1(I) 2) "xÎI: (x, j1(x),.., jn(x))ÎW 3) "xÎI: d j(x) /dx= f( x. j(x)) Определение Пусть (j1(x),.., jn(x)) T решение системы (1) на I. Интегральной кривой системы (1) называется кривая g Î Rn+1x,y1,..,yn, заданная параметрически: g={x=x; y1=j1(x);…; yn=jn(x)}, xÎI
Задача Коши Пусть f (x, y)=(f1(x, y),.., fn(x, y))T определена в W и точка (x0,y01,..,y0n)ÎW Найти решение j(x) =(j1(x),.., jn(x)) системы (1) [(2)], удовлетворяющее условиям j1(x0)=y01, j2(x0)=y02,.., jn(x0)=y0n. Запись в векторном виде: Обозначим y 0=(y01,..,y0n)ÎRn Задача Коши d y /dx= f( x. y) – система, y (x0)= y 0 – начальное условие. Геометрический смысл: - найти интегральную кривую, проходящую через эту точку Теорема (ТСЕ для НС n) Пусть f (x, y)=(f1(x, y),.., fn(x, y)) и ¶ f (x, y)/¶yi=(¶f1/¶yi,..,¶fn/¶yi), где i=1,..,n определена и непрерывна в области WÎRn+1x,y1,..,yn и (x0,y01,..,y0n)= (x0, y0)ÎW Тогда на некотором интервале I=(x0-d,x0+d) существует решение задачи Коши. d y /dx= f( x. y), y (x0)= y 0 и это решение единственно. (без доказательства)
Устойчивый фокус
а)
спирали
Неустойчивый фокус
38. Исследование устойчивости положения покоя системы двух ЛДУ с постоянными коэффициентами в случае
Точки покоя:
det(A-λE) = 0
1) Матрица А имеет 1 линейно независимый собственный вектор (к
а) асимптоти-чески устойчивая система
Устойчивый вырожденный узел б)
2) Матрица А имеет 2 линейно независимых собственных вектора
a) асимптотически устойчивая система
б) Формулировка теоремы существования и единственности (ТСЕ). Понятие общего решения. Обобщение некот понятий. Пусть f(x,y) опред обл DÌR2 X,Y, точка (x0,y0)ÎD. Рассмотрим задачу Коши (8)(y’=f(x,y)(2);y(x0)=y0). Пусть j1(x) и j2(x) решения (8), т.е. j1(x),j2(x)-реш(2) и j1(x0)=y0, j2(x0)=y0. Опред. Говорят, что задача Коши(8) имеет единст решение если любые 2 реш j1(x) и j2(x) этой задачи совпадают на некот окр-сти точки x0 $d>0 "xÎ(x0-d,x0+d):j1(x)ºj2(x) ТСУ1(Локальная) Пусть на обл. DÌR2 X,Y функ.f(x,y) и ее част. производная (¶x/¶y)(x,y) опред. и непрерывны, и точка (x0,y0) ÎD. Тогда урав. y’=f(x,y) имеет решение j(x): 1)опред. на некот. окр-сти (x0-h,x0+h) точки x0, удовл. условию j(x0)=y0; 2)такое решение единственно.(Без док-ва) Замечание к ТСЕ. Пусть в обл D выполн. усл. ТСЕ1. 1)В D беск много решений уравнений. x0-точка(x0,y0)ÎD.Через эту точку проходит реш y=j(x,y0).Все эти решения не совпадают. 2)Решение задачи(8) может быть опред-но лишь на некот окр-сти x0. Пусть f(x,y) удовл в D условиям ТСЕ1. Функцию y=j(x,c) наз-ют общим решения урав(2) в обл D, если: 1)"c:j(x,c)-реш(2); 2)" частное решение урав(2) может быть получено из j(x,c) подбором соотве-его значения c. 2. ОДУ первого порядка, разрешенные относительно производной. Понятия решения и интегральной кривой уравнения. Постановка задачи Коши. Пусть область DÌR2 и f(x,y) определена в D. y’=f(x,y) (1) - ОДУ 1-го порядка разрешенная относительно производной. Опр 1. Функция y=j(x) определена на промежутке I=<a,b> называется решением уравнения (1) если: 1) j(x)ÎC1(I); 2) "xÎI:(x,j(x))ÎD 3)"xÎI: j'(x)=f(x,j(x)). Опр 2. Если y=j(x)- решение (1), то график этой функции называется интегральной кривой уравнения (1).
Постановка задачи Коши. Известно: Область DÌR2, f(x,y)-определена в D и точка (x0,y0)ÎD (или числа (x0,y0)ÎD).Надо найти решения y=j(x) уравнения (1) определенное на I, такое что j(x0)=y0 (т.е. интегральная кривая проходящая через (x0,y0)). Числа (x0,y0) называются начальными условиями.
|
|||||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 339; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.24.57 (0.009 с.) |

 |R2Опред.1| Пусть P(x,y) и Q(x,y) непрерывны в обл.D. Кривая γ ={(x,y), x=φ(t), y=ψ(t), t
|R2Опред.1| Пусть P(x,y) и Q(x,y) непрерывны в обл.D. Кривая γ ={(x,y), x=φ(t), y=ψ(t), t 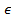 I=< α, β>} называется интегральной кривой ур-я (1)P(x,y)dx+ Q(x,y)dy=0,если выполняются условия:
I=< α, β>} называется интегральной кривой ур-я (1)P(x,y)dx+ Q(x,y)dy=0,если выполняются условия: I: (φ(t), ψ(t))
I: (φ(t), ψ(t))  I: P((φ(t), ψ(t)) φ (1)(x)+Q((φ(t), ψ(t)) ψ(1)(t)≡0
I: P((φ(t), ψ(t)) φ (1)(x)+Q((φ(t), ψ(t)) ψ(1)(t)≡0 : Ф(х,у)=С – интеграл ур-я (1);2) Любой интеграл ур-я можно получить подбором соответствующих произвольныз постоянных С.
: Ф(х,у)=С – интеграл ур-я (1);2) Любой интеграл ур-я можно получить подбором соответствующих произвольныз постоянных С.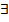 U(x,y)
U(x,y)  U(x,y)=С. Докажем что U(x,y)=С – общий интеграл ур-я(2): пусть γ ={(x,y), x=х(t), y=у(t), t
U(x,y)=С. Докажем что U(x,y)=С – общий интеграл ур-я(2): пусть γ ={(x,y), x=х(t), y=у(t), t 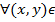 γ: U(x,y)=C
γ: U(x,y)=C ;
;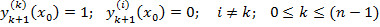

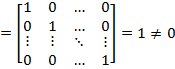
 — линейно независимы (по следствию 4)
— линейно независимы (по следствию 4) =Re
=Re  ,
, Система неустойчива; фазовые траектории: раскрученные
Система неустойчива; фазовые траектории: раскрученные ,
, 
 A=
A=  ,
,


 ,
, 
 , единственная точка покоя (0,0).
, единственная точка покоя (0,0). =0 – характеристическое уравнение.
=0 – характеристическое уравнение. – корни характеристического уравнения.
– корни характеристического уравнения. кратные корни
кратные корни =
=  +
+ 
 -собственный вектор, отвечающий
-собственный вектор, отвечающий 
 )
)

 неустойчивая система
неустойчивая система Неустойчивый вырожденный узел
Неустойчивый вырожденный узел ,
, 
 +
+  =
= 

 ,
,  y=
y=  x
x ,
, устойчивый дикритический узел
устойчивый дикритический узел


