
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные уравнения первого порядка. Уравнения Бернули.Содержание книги
Поиск на нашем сайте
Ур-е вида(1) y/ + p(x)=f(x) – линейное ур-е 1ого порядка. Теор. Пусть функция р(х) и f(x) непрерывны на интервале α<x<β. Тогда через любую точку(х0;у0) полосы D={(х;у); α<x<β, -∞<y<+∞}проходит единственное решение ур-я (1) причем оно определено на (α;β). Уравнение(1) однородное, если f(x)≡0 и неоднородно в противном случае. Док-во(Метод решения): 1) Пусть ур-е однородное, т.е y/ + p(x)=0 – это ур-е с разделяющимеся переменными. у≡0 – решение; у≠0, dy/y=-p(x)dx, ∫dy/y=-∫p(x)dx,ln|y|=-∫x0X p(t)dt + lnC1, C1>0, lnC1 ϵ |R Потенциируем выражение |y|=C1exp(-∫x0X p(t)dt), y=± C1exp(-∫x0X p(t)dt), C1>0 {C1,y>0 => Введем новую С={-C1,y<0 => y=Cexp(-∫x0X p(t)dt), разрешим С=0,С ϵ |R Решение проходит через(х0;у0) имеет вид y = y0exp(-∫x0X p(t)dt) 2) Пусть f(x)≠0/ Решаем ур-е (1) Выпишем все решение ур-я y/ + p(x)=0, y=Cexp(-∫x0X p(t)dt), оно представляется в виде у= φ(x). Св-ва φ(x):1) φ(x) ϵ С1(α;β) 3) φ(x) – решение уравнения y/ + p(x)=0 на (α;β), т.е Подставим у=φ(x)С(х) в (1) y(1)=C(1)(x)φ(x)+C(x) φ (1)(x), [C(1)(x)φ(x)+C(x) φ (1)(x)]+p(x)C(x) φ(x)=f(x), т.к C(1)(x)φ(x)+ p(x)C(x) φ(x) ≡0, то C(1)(x)φ(x)=f(x), т.к φ(x)>0 на(α;β) C(1)=f(x)/ φ(x) – непрерывно на (α;β) С(x)= ∫x0Xf(s)/ φ(s)dS + K,K ϵ|R Подставим С(x) в y(x): y(x)= φ(x) ∫x0Xf(s)/ φ(s)dS + K φ(x) Замечание| yо.н=уо.о+уч.н Решение проходит через(х0;у0), y(x)= φ(x) ∫x0Xf(s)/ φ(s)dS + у0 φ(x)=>y(x0)= φ(x0) ∫x0X0f(s)/ φ(s)dS + у0 φ(x0)=0+y0*1=y0 Ур-е вида(2) y/ + p(x)=y(n)f(x)- ур-е Бернули. n≠0,n≠1. Если n>0,то y≡0 – решение, =>y≠0 то делим обе части ур-я на y(n), Вводим новую переменную z(x)=y(1-n), z(1)(x)= (y(1-n))(1)=(1-n)y(-n)y(1), z(1)+(1-n)p(x)z=(1-n)f(x) – линейное относ. z
4. Уравнения с разделяющимися переменными. Однородные уравнения. Уравнения с разделяющимися переменными: y’=f(x)*g(y) (3) Теорема 1. Пусть функция f(x)-непрерывна на интервале (a,b), а функция g(y)-непрерывна на (c,d) причем для "yÎ(c,d): g(y)¹0. Тогда через любую точку прямоугольника D={(x,y),a<x<b,c<y<d} проходит единственное решение уравнения (3). Док-во. y’=f(x)*g(y) (3); g(y) ≠0; (3’): y’/g(y)=f(x). Проинтегрируем (3’) по х òy’dx/g(y)=òf(x)dx ó òdy/g(y)= òf(x)dx (3*) Это равенство множества первообразных. Обозначим F(x)= x0òxf(t)dt, G(y)= y0òyds/g(s). Из (3*) G(y)=F(x)+C. Т.к. G’(y)=1/g(y)≠0, то у G(y) существует обратная G-1. y= G-1(F(x)+C)-решение урав(3). Найдем реш., прох. (x0,y0). G(y0)=F(x0)+C -> 0=0+C=0. y=G-1(F(x)) проходит через (x0,y0).
Теор1| Пусть D-односвязная область в |R2x,y функции P(x,y),Q(x,y) непрер. И диффер. на D. Тогда ур-е P(x,y)dx+ Q(x,y)dy=0 явл. ур-ем в полных диффер., если Док-во:1) Необходимость. Пусть ур-е явл. ур-ем в полных диффер.,т.е dU= P(x,y)dx+ Q(x,y)dy. Известно что dU=U(1)x dx+ U(1)y dy значит
Нахождение первообразной: dU(x,y)= P(x,y)dx+ Q(x,y)dy=0- ур-е в полных диффер.; dU=U(1)xdx+ U(1)ydy,т.е U(1)x=Р(х,у), U(1)y=Q(x,y), U(x,y)=∫P(x,y)dx+ g(y), g(y)-непр.диффер.подлежит определению.
7. Уравнения первого порядка, не разрешенные относительно производной. Пусть в обл. в G Рассмотрим функцию F(x,y,U1) опред. на G Постановка задачи Коши: Пусть F(x,y,p) опред.в обл. в G Опред| Решение ур-я F(x,y,у(1))=0, через каждую точку которого, проходит ещё одно решение, касаясь того же направления, называется особым решением этого ур-я. Общий метод введения параметра. F(x,y,у(1))=0 ур-е 1ого порядка неразреш. отн. производной. Будем искать решение (интегральную кривую) в параметрическом виде(2) γ {х=х(р), у=у(р), рϵ < α, β>. Вводим параметр у(1)=р. Сводим уравнение к разрешенному отн. производной у=f(x, у(1)) или x=g(y, у(1)). Решение ищем в виде γ {х=х(р), у=у(р), γ {х=х(р), у=f(x(р),p), p=p(x), p(1)(x)≠0. Рассм. равенство: у=f(x,p) и продиффер. его по х,считая р=р(х); (1*) рх(1)р=
Уравнения Лагранжа и Клеро. Ур-ие Лагранжа: y=f(y’)*x+g(y’) (1); f(y’) ≠y’; y’=p; {x=x(p),y=y(p); {x=x(p),y=f(p)*x+g(p); yx’=f(p)+x*df/dp* px’+dg/dp* px’; p-f(p)=x*df/dp* px’+dg/dp* px’; Если p-f(p) ≠0 и т.к. px’≠0; (p-f(p))* xp’=x*df/dp+dg/dp лин. ур-ие относит. x(p). Если сущ-ет p0 такое, что f(p0)= p0=0, т.е. f(p0)= p0
то ур-ие (1) имеет реш-ие вида; y=f(p0)+g(p0) или y= p0*x+g(p0)); Ур-ие Клеро: y=x*y’+g(y’)(2); вводим параметр p=y’; {x=x(p), y=x*p+g(p); yx’=p+x* px’+ gp’*px’; p = p + x*px’ + gp’*px’; [x + gp’(p)]*px’ = 0; a) px’=0 óp=c; y=c*x+g(c) семейство прямых(реш ур-ия (2)); б) x+g’(p)=0óx=-g’(p); Уравнение интегральной кривой γ: {x = - g’(p); y = - p*g’(p) + g(p); Пусть g(p) ЄC1(I), g’’≠0; в этом случае γ-особая интег-ая кривая(2), пусть p0Є I: (x0;y0) Є γ; { x0 =-g’(p0), y0=- p0g’(p0)+g(p0) Для γ в точке (x0;y0) yx’ - тангенс угла наклона касательной yx’ (x0;y0)= p0; y=c*x+g(c); {x0=-g’(p0), y0=- p0*g’(p0)+g(p0)=c* x0+g(c); yx’(x0)= p0=c; c= p0; реш-ие y= p0*x+g(p0) проходит через точку (x0;y0) касаясь интегр-ой кривой особая инт-ая кривая γ ó γ-особая интегр-ая кривая.
|
||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 270; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.224.236 (0.01 с.) |

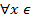 (α;β): φ(x)>0. 2) φ(x0)≡ exp(-∫x0X0 p(t)dt)=1
(α;β): φ(x)>0. 2) φ(x0)≡ exp(-∫x0X0 p(t)dt)=1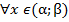 φ (1)(x)+p(x) φ(x)≡0. Решение уравнения (1) ищем в виде y=C(x) φ(x),где С(x)непрерывно дифференцируема на (α;β),подлежит определению.
φ (1)(x)+p(x) φ(x)≡0. Решение уравнения (1) ищем в виде y=C(x) φ(x),где С(x)непрерывно дифференцируема на (α;β),подлежит определению.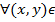 D:
D: 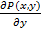 =
= 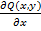 .
.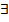 U(x,y)
U(x,y) 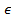 C1(D)
C1(D)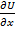 =P(x,y);
=P(x,y); 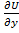 =Q(x,y). P,Q
=Q(x,y). P,Q  =
= 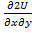 ,
, 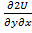 , т.к
, т.к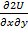 и
и 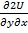 - непр. То.
- непр. То. 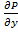 =
=  .
.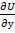 =
= 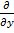 (∫P(x,y)dx+ g(1)(y))= Q(x,y). Сначала находим g(1)(y) и g(y) и подставляем g(y) в U(x,y).
(∫P(x,y)dx+ g(1)(y))= Q(x,y). Сначала находим g(1)(y) и g(y) и подставляем g(y) в U(x,y).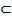 |R3х,у,р опред. непр. Функция F(x,y,p) и ур-е F(x,y,p)=0 имеет хотя бы 1 решение в обл. G. Говорят,что урав. F(x,y,p)=0 задает в обл. D
|R3х,у,р опред. непр. Функция F(x,y,p) и ур-е F(x,y,p)=0 имеет хотя бы 1 решение в обл. G. Говорят,что урав. F(x,y,p)=0 задает в обл. D 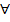 (x,y)ϵD: ((x,y),f(x,y))ϵG. 2)
(x,y)ϵD: ((x,y),f(x,y))ϵG. 2)  =
=  +
+  т.к
т.к 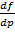 . Решаем (1*), находим х(р), подставляем в (2).
. Решаем (1*), находим х(р), подставляем в (2).


