Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейно зависимые и линейно независимые системы функций. Определитель Вронского и необходимое условие линейной зависимости произвольной системы функций.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определитель Вронского системы ф-ций. Услов. линейной зав ф-ции. 1)Пусть ф-ции х 2)Функ. Пусть y1(x),y2(x)… Опр-ль вида W(x)=W(y1(x),y2(x)… Наз-ся опред-лем Вронского
Теорема об определителе Вронского системы линейно независимых решений однородного ЛДУ порядка n. Т1 Пусть решения y1(x),y2(x)… Если y1(x),y2(x)…
Следствие: Если сущ-т X0, такое, что W(Х0)=0, то y1(x),y2(x)… ФСР однородного ЛДУ с постоянными коэффициентами в случае, когда характеристическое уравнение имеет кратные корни. L[y]=y^{n}+a1y^{n-1}+…+a(n-1)y’+an*y=0 (13) l(t)=t^n+a1t^(n-1)+…+a(n-1)t+an (15) Определение Говорят, что число lÎC является корнем кратности k многочлена l(t) степени (n-k), если l(t)=(t-l)^k*l1(t), где l1(l)¹0. Если k=1, l- простой корень. L=l(D)=D^n+a1*D^(n-1)+…+a(n-1)*D+an. Пусть l - корень кратности k l(t), т.е. l(t)=(t-l)^k*l1(t), то L=l(D)=(D-l)^k*l1(D)=l1(D)*(D-l)^k.Зафиксируем sÎN èø s=0 (натуральные и ноль) x^s*e^lx, (D-l)^k*[x^s*e^lx] 1. k=1 (D-l)^k*[x^s*e^lx]==(det) D*[x^s*e^lx]-l*[x^s*e^lx]= =(d/dx)*[x^s*e^lx]-l*[x^s*e^lx]= =s*x^(s-1)*e^lx+l*[x^s*e^lx]-l*[x^s*e^lx]=s*[x^(s-1)*e^lx] (D-l)*[x^s*e^lx]=[s*[x^(s-1)*e^lx], sÎN; 0, s=0] 2. (D-l)^2*[x^s*e^lx]= (D-l)*[(D-l)*[x^s*e^lx]]= =(D-l)*[s*x^(s-1)*e^lx]=s*(D-l)*[x^(s-1)*e^lx]= =[s*(s-1)*[x^(s-2)*e^lx], s>1; 0, 0<=s<=1] kÎN. (D-l)^k*[x^s*e^lx]=[k*(k-1)*…*(k-s+1)[x^(s-k)*e^lx], s>=k; 0, 0<=s<=k-1] Теорема 1: Пусть lÎC явл. корнем кратности k храк-кого многочлена, тогда функции e^lx, x*e^lx,..,x^(k-1)*e^lx являются решениями (13) Доказательство (13) L[y]=0 L=l[D]=l1(D)* (D-l)^k 0<=s<=k-1: L[x^s*e^lx]=(l1[D]* (D-l)^k)*[x^s*e^lx]=l1(D)*((D-l)^k*[x^s*e^lx])= l1(D)[0]=0, т.к. 0<=s<=k-1. => x^s*e^lx- реш. (13) Лемма: Для любых различных l1,l2,..,lsÎC и k1,k2,..,ksÎN, тогда система функций {e^l1x, x*e^l1x,..,x^(k1-1)*e^l1x; e^l2x, x*e^l2x,..,x^(k2-1)*e^l2x;…; e^lsx, x*e^lsx,..,x^(ks-1)*e^lsx} линейно независима на R Теорема Пусть различн. числа l1,l2,..,lsÎC - корни характеристического многочлена l(t) кратности k1,..,ks соответственно и k1+…+km=n. Тогда обще решение (13) имеет вид y(x)=P1(x)*e^l1x+…+Ps(x)*e^lsx, где "j=1,..,s Pj(x) – многочлен степени kj-1, коэффициентами которого являются произвольные комплексные числа. Доказательство т.к. "ljÎC, j=1,..,s –корень хар-го многочлена l(t), то по Th 1 функции: e^l1x, x*e^l1x,..,x^(k1-1)*e^l1x; e^l2x, x*e^l2x,..,x^(k2-1)*e^l2x;…; e^lsx, x*e^lsx,..,x^(ks-1)*e^lsx – решения (13). По Лемме эти ф-ции явл. линейно независ. на R. Число этих функций k1+k2+…+km=n. Следовательно, они образуют ФСР. yо.о.= j=1ås (C1j+C2j*x+…+C(kj)j*x^(kj-1))*e^ljx, где С – произвольные комплексные числа.
Действительный случай Пусть a1,..,anÎR (17) L[y]=y{n}+a1*y{n-1}+…+a(n-1)*y’+an*y=0 (15) l(t)=t^n+a1*t^(n-1)+…+a(n-1)*t+an=0
ФСР однородного ЛДУ с постоянными коэффициента-ми в случае простых корней характеристического уравнения (действительных или комплексных). Теорема1: Пусть a1,..,anÎC и L[y]=y{n}+a1*y{n-1}+…+a(n-1)*y’+an*y=0 (13) и l(t)=t^n+a1*t^(n-1)+…+a(n-1)*t+an (15)– характеристический многочлен ОЛДУ(13). Функция e^lx, где lÎC, Является решением (13) т. и т. т., когда l(l)=0 (т.е. l - корень характеристического многочлена (13)) Доказательство Т.к. L[e^lx]= D^n*[e^lx]+…+ a(n-1)*D*[ e^lx ]= e^lx*(l^n +…+ a(n-1) *l + an) = e^lx * e(l)=0 <=> e[l]=0 Лемма Пусть l1, l2,.., lnÎC, причем li¹lj при i¹j. Тогда функции e^l1x, e^l2x,.., e^lnx линейно независимы на R Доказательство: Индукция по n: 1) n=1 a1*e^l1x=0 <=> a1=0 – утверждение верно 2) Пусть для попарно независ. M1,..,M(n-1)- утверждение верно 3) li¹lj, " i¹j, e^l1x, e^l2x,.., e^lnx. Пусть"xÎR и a1,.., anÎC a1*e^l1x+a2*e^l2x+…+an* e^lnxº0, умножим на e^(-lnx) "x: a1* e^(l1-ln)x+…+a(n-1)*e^(l(n-1)-ln)x + anº0. Дифференцируем (l1-ln)*a1*e^(l1-ln)x+…+(l(n-1)-ln)*a(n-1)*e^(l(n-1)-ln)xº0 Т.к.: l1-ln¹…¹l(n-1)-ln, то п индуктивному предположению => e^(l1-ln)x,..,e^(l(n-1)- ln)x – линейно независимы на R Замечание: (li-ln)aiº0, i=1,..,(n-1) => a1=a2=…=a(n-1)=0 an*e^lnxº0=> an=0 => e^l1x,…, e^lnx. Теорема2: Пусть a1,..,anÎC и (13) l(t)=t^n+a1t^(n-1)+…+a(n-1)t+an – характеристический многочлен уравнения (13). Если l1,l2,..,lnÎC – корни характеристического многочлена (15) такие, чтоli¹lj при i¹j, то функции e^l1x, e^l2x,.., e^lnx образуют ФСР ур-ния(13) и общее решение им. вид: y(x)=C1e^l1x+ C2e^l2x+…+ Cn*e^lnx (16), где C1,..,Cn – произвольные комплексные постоянные. Доказательство: Т.к. l1,…, ln-корни хар.ур.(15), то по теореме 1:e^l1x, e^l2x,.., e^lnx – решения (13) По Лемме 4, т.к. li¹lj, i¹j, то e^l1x, e^l2x,.., e^lnx – линейно независимы => e^l1x, e^l2x,.., e^lnx – ФСР (13) И значит, общее решение (13) имеет вид (16) Действительный случай Пусть a1,..,anÎR (действительные числа). l(t)=t^n+a1t^(n-1)+…+a(n-1)*t+an – многочлен с действительными коэффициентами. Пустьl1, l2,.., ln (li¹lj, i¹j)-корни этого многочлена. а) l1, l2,.., lnÎR, тогда ФСР e^l1x, e^l2x,.., e^lnx – действительная функция y(x)=C1e^l1x+ C2e^l2x+…+ Cn*e^lnx, где С1,..,Сn – произвольные действительные числа
|
|||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 432; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.78.108 (0.008 с.) |

 наз-ся лин зав-ми на I, если найдутся числа
наз-ся лин зав-ми на I, если найдутся числа  не все равные нулю, такие, что на I выполняется тождество:
не все равные нулю, такие, что на I выполняется тождество: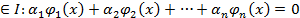
 наз-ся лин. незав. на I, если выполн тожд-во:
наз-ся лин. незав. на I, если выполн тожд-во: 
 (I)
(I)
 )=
)= 
 – лин незав на I.
– лин незав на I.