
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Совместность линейных систем.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение 4.5. Линейная система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Определение 4.6. Совместная линейная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. Назовем расширенной матрицей системы (2.2) матрицу вида
Теорема Кронекера-Капелли. Система (2.2) совместна тогда и только тогда, если ранг матрицы системы равен рангу расширенной матрицы.Доказательство.Необходимость: пусть система (2.2) совместна и 1) Достаточность: если Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения. Решение системы линейных уравнений матричным методом Еще один, пользующийся большой популярностью метод. Этот способ или, как его еще называют, метод обратной матрицы называется так потому, что все решение сводится к простому матричному уравнению, для решения которого необходимо найти обратную матрицу. Для того, что бы расставить все точки над и, рассмотрим метод под микроскопом. Алгоритм решения достаточно просто. Как и в методах Гаусса и Крамера первоначально надо проверить, имеет ли система уравнений решение по теореме Кронекера-Копелли. Затем для решения матричным методом необходимо ввести в рассмотрение матрицы-столбцы для неизвестных X и свободных членов B. Тогда систему линейных уравнений можно записать в матричной форме AX=B. Умножив это матричное уравнение на A-1, получим A-1AX= A-1B, откуда EX=X=A-1B. Следовательно, матрица-решение X легко находится как произведение A-1 и B.Для большей ясности решим небольшой пример методом обратной матрицы:
21x1-45x2-3.5x3=10 12x1-16x2+21x3=-16 14x1+13x2-8x3=10 Определим совместность системы уравнений. По теореме Кронекера-Копелли для того, что бы система линейных алгебраических уравнений была совместна (имела решение), необходимо и достаточно, чтобы ранг основной матрицы
и ранг расширенной матрицы
были равны.Так как rang|A|=3 равен rang|B|=3 и равен количеству неизвестных n=3, то система имеет единственное решение.Для решения методом обратной матрицы необходимо ввести матричные обозначения
Найдем обратную матрицу A-1. Как ее найти, показывать не будем. Воспользовавшись нашии онлайн калькулятором, вы сможете выбрать один из двух способов для ее нахождения. Она будет иметь вид.
Для нахождения матрицы X умножим обратную матрицу А-1 на матрицу С
Получили решение системы уравнений Правило Крамера. Рассмотрим систему (2.3). Назовем главным определителем этой системы определитель
Предположим сначала, что Сложив затем все уравнения, получим:
Отметим, что (j-й столбец) (Результат получен из разложения определителя по j-му столбцу). Такой определитель равен 0 при Предположим теперь, что В этом случае, если все
Таким образом, правило Крамера позволяет найти единственное решение системы (2.3) или сделать вывод о существовании бесконечного числа решений либо об их отсутствии: 2) Если 3) Если 4) Если
Вопрос 5 1) Минор n-ого порядка.
2) Ранг матрицы. Ответ 1. Рангом матрицы Единое, стандартное, обозначение ранга матрицы отсутствует. Однако ув. Глухов показывал нам, что он обозначается как rang A (основной) и rang A (“A” с черточкой наверху – расширенный ранг), позже покажу. 2. Теперь то, что касается ранга матрицы.
Теперь возвращаемся к рангам. Вспоминаем, что ранг – это НАИБОЛЬШИЙ из порядков МИНОРОВ. Всего таких порядков может быть дохуища, все зависит от того, насколько огромна матрица. В данной матрице порядков будет не более 3, но еще неизвестно, сколько из них будут не равны нулю. Начинаем по порядку. Ищем миноры ПЕРВОГО порядка. Таковым является любое число в матрице.
Таким образом 1,4,5 у меня миноры ПЕРВОГО порядка. Ищем миноры ВТОРОГО порядка. Это будет пересечение строк и столбцов (т.е. то, что мы рассматривали выше). Найдем минор 3 строки 3 столбца.
Дальше рассматриваем минор третьего порядка. Это определитель который мы считали треугольниками.
Видим, что максимальный порядок, т.е. ТРЕТИЙ - НЕ РАВЕН (если бы 3ий порядок был равен нулю, было бы rang=2) нулю, следовательно ранг матрицы = 3 (rang A = 3) Думаю, с этим понятно. Ну это трудный способом, но эффективный, можно посчитать так. Запоминаем, что РАНГ матрицы соответствует НАИБОЛЬШЕМУ порядку не равному нулю. Т.е. если бы у нас определитель третьего порядка был бы =0, то у нас было бы rang A= 2 Есть еще одна фишка. Можно привести матрицу вида
К треугольной, получим
Видно, что число НЕНУЛЕВЫХ строк, равно 3 => rang = 3 это основной ранг матрицы. Но есть и РАСШИРЕННЫЙ. Например, если бы у нас была бы матрица:
То расширенным рангом называлась бы область, которая включает все нули (т.е. 4 столбец), но тем не менее видим, что НУЛЕВЫХ строк нет, следовательно ОСНОВНОЙ ранг равен 3 и ранг РАСШИРЕННЫЙ равен 3 Ну понятно, что если 82.799 было бы равно нулю, то ранг был бы соответственно равен 2. С рангами все, дальше. 3) Теорема Кронекера–Капелли (критерий совместности системы линейных уравнений). Ответ Для того чтобы система линейных уравнений была совместной, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу ее расширенной матрицы, т.е. Замечание. Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение, если же ранг меньше числа неизвестных, то система имеет множество решений. (об этом позже, это неопределенности) Начнем с охуительного примера. Пример 13. Исследовать систему линейных уравнений Решение. Составим расширенную матрицу системы и с помощью элементарных преобразований вычислим одновременно ранги обеих матриц.
Далее умножим вторую строку на -2 и сложим с третьей, а затем сложим третью строку с последней. Имеем
Вспомнили как решается матрица методом гаусса? Идем дальше. Нас интересует это:
Выше я объяснял, что такое ранг ОСНОВНОЙ и ранг РАСШИРЕННЫЙ. Так вот, согласно теореме Кронекера-Капелли, данная будет несовместной, так как rang A (основной) = 3 (т.к. кол-во НЕНУЛЕВЫХ строк равно 3), а rang A (с черточкой над А, расширенный) = 4. Доказывается эта теорема на примере обычной матрицы, думаю ни у кого не составит труда накалякать матрицу и объяснить. Для танкистов, которые еще не поняли ОСНОВНОЙ и РАСШИРЕННЫЙ ранги: 4) Определенность-неопределенность Ответ Исследовать систему линейных уравнений – означает определить, какой является эта система – совместной или несовместной, и в случае её совместности выяснить, определённая эта система или неопределённая. Условие совместности системы линейных уравнений даёт следующая теорема
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 701; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.180.177 (0.012 с.) |

 , а матрицей системы – матрицу из коэффициентов при неизвестных.
, а матрицей системы – матрицу из коэффициентов при неизвестных. ее решение. Тогда
ее решение. Тогда  , то есть столбец свободных членов является линейной комбинацией столбцов матрицы системы и, следовательно, столбцов любого ее базисного минора. Поэтому добавление элементов этого столбца и любой строки расширенной матрицы к базисному минору даст нулевой определитель, то есть
, то есть столбец свободных членов является линейной комбинацией столбцов матрицы системы и, следовательно, столбцов любого ее базисного минора. Поэтому добавление элементов этого столбца и любой строки расширенной матрицы к базисному минору даст нулевой определитель, то есть 
 то любой базисный минор матрицы А является и базисным минором расширенной матрицы. Поэтому столбец свободных членов представляет собой линейную комбинацию столбцов этого базисного минора, и, следовательно, линейную комбинацию всех столбцов матрицы А. Если обозначить коэффициенты этой линейной комбинации
то любой базисный минор матрицы А является и базисным минором расширенной матрицы. Поэтому столбец свободных членов представляет собой линейную комбинацию столбцов этого базисного минора, и, следовательно, линейную комбинацию всех столбцов матрицы А. Если обозначить коэффициенты этой линейной комбинации 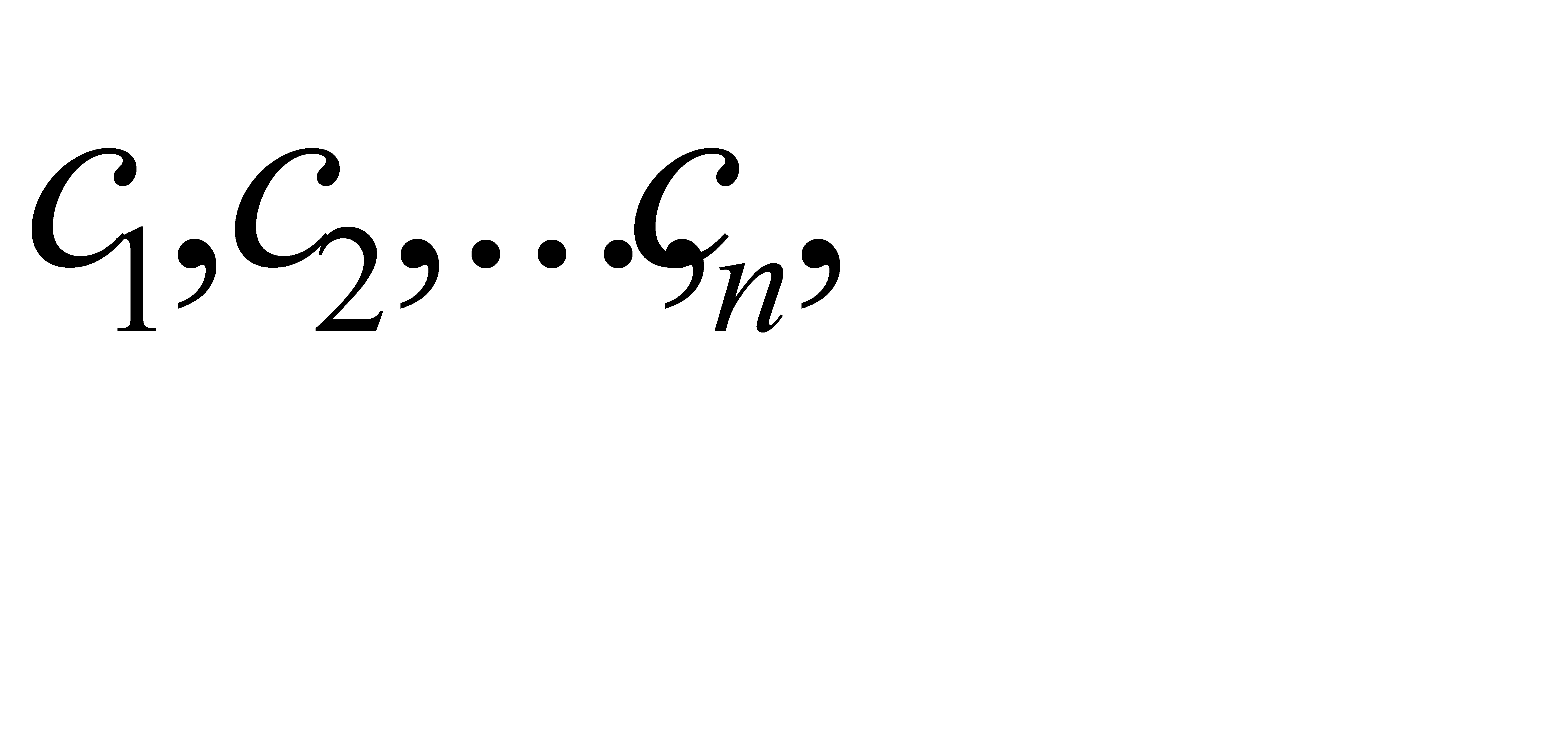 то эти числа будут решением системы (2.2), т.е. эта система совместна. Теорема доказана.
то эти числа будут решением системы (2.2), т.е. эта система совместна. Теорема доказана. , элементами которого являются коэффициенты при неизвестных:
, элементами которого являются коэффициенты при неизвестных:
 .
. Умножим каждое уравнение системы (2.3) на алгебраические дополнения
Умножим каждое уравнение системы (2.3) на алгебраические дополнения  элементов j-го столбца
элементов j-го столбца 
 . (2.5)
. (2.5) .
.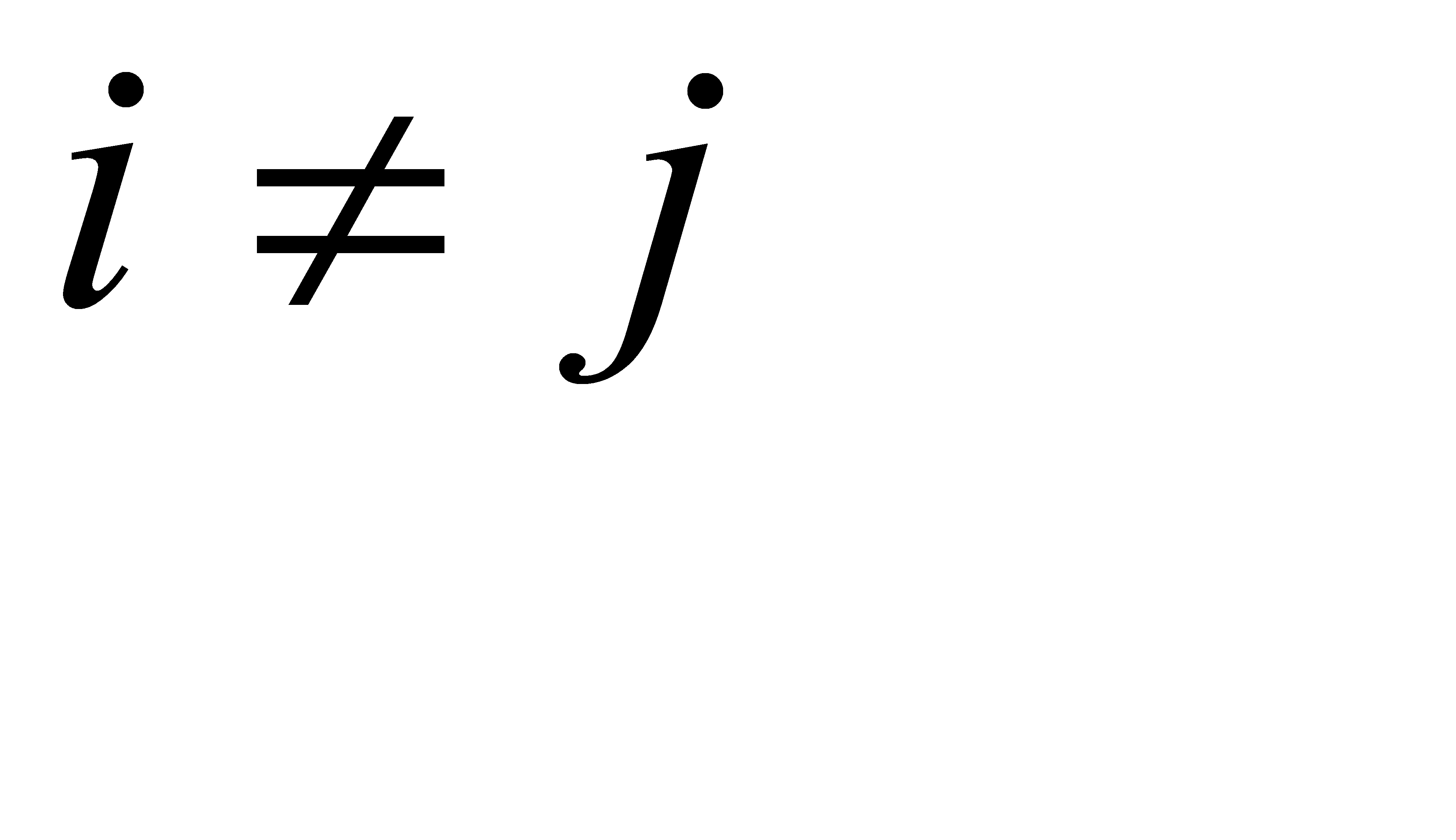 и равен
и равен  . Рассматривая j = 1,2 ,…,n, получим систему, эквивалентную исходной:
. Рассматривая j = 1,2 ,…,n, получим систему, эквивалентную исходной: 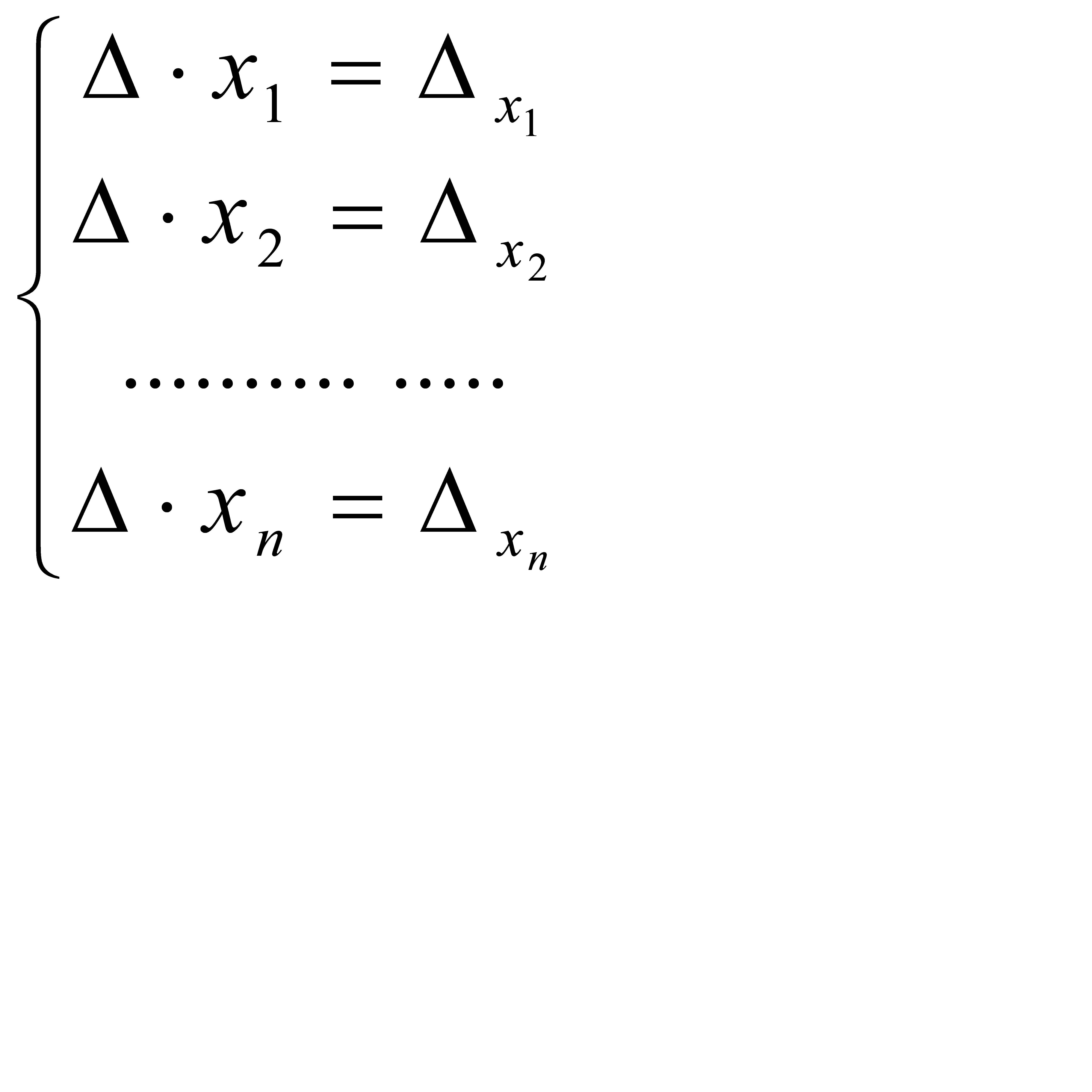 (2.6). Разделив все уравнения на
(2.6). Разделив все уравнения на  .
.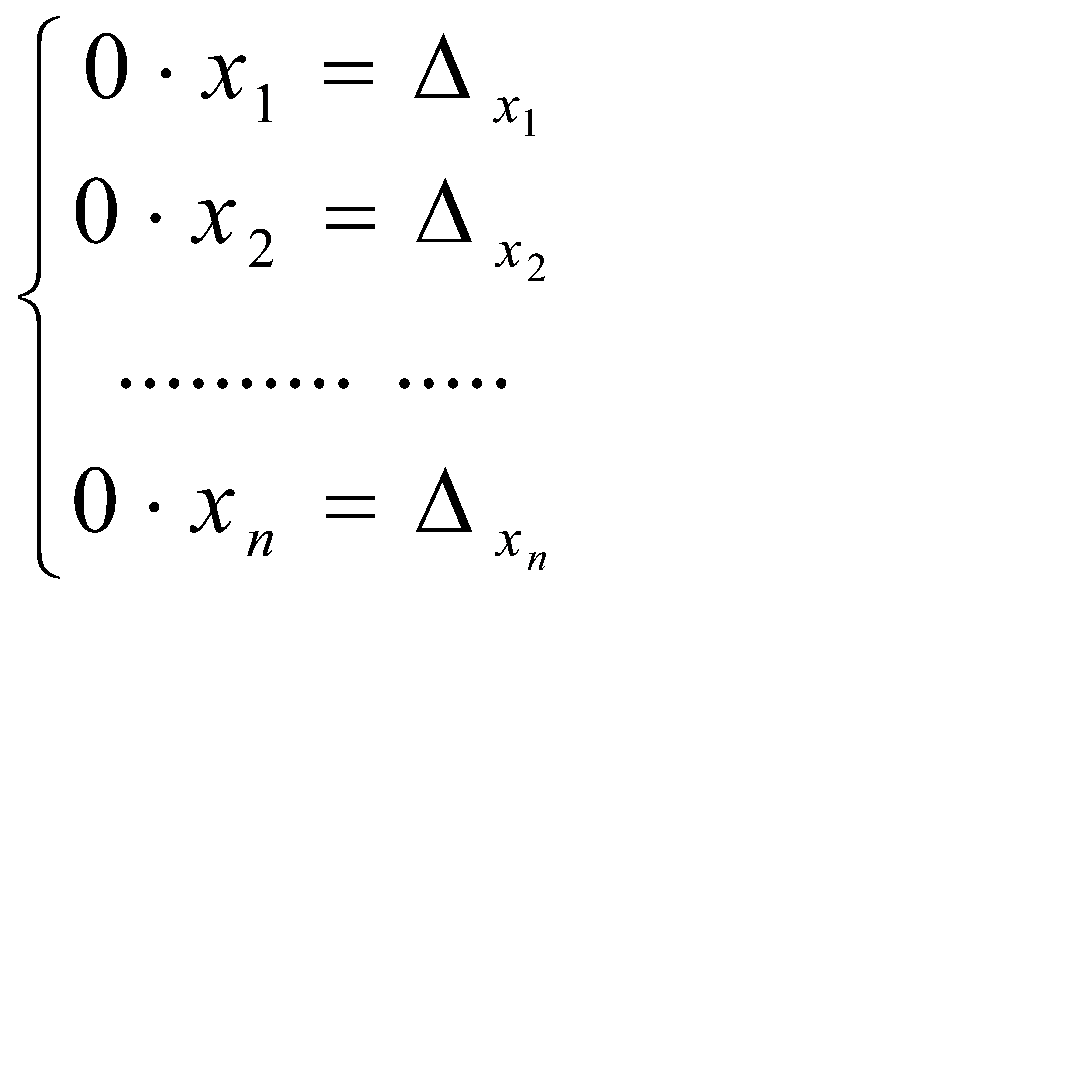 .
. и имеет бесконечно много решений. Если же хотя бы один из
и имеет бесконечно много решений. Если же хотя бы один из  система решений не имеет.
система решений не имеет.
 называется наибольший из порядков миноров матрицы
называется наибольший из порядков миноров матрицы 


 Считаем получаем -2 не равное 0.
Считаем получаем -2 не равное 0.
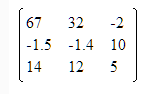


 . В противном случае система не совместна.
. В противном случае система не совместна.

 .
.



