
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства линейно зависимых и линейно независимых векторовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 1. Если в систему векторов входит нулевой вектор, то она линейно зависима 2. Если в системе векторов имеется два равных вектора, то она линейно зависима. 3. Если в системе векторов имеется два пропорциональных вектора 4. Система из 5. Любые векторы, входящие в линейно независимую систему, образуют линейно независимую подсистему. 6. Система векторов, содержащая линейно зависимую подсистему, линейно зависима. 7. Если система векторов Тогда из равенства Следовательно, линейная комбинация векторов Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов. Пространство, имеющее конечную размерность, называется конечномерным. Пространство, в котором можно найти сколь угодно много линейно независимых векторов, называется бесконечномерным. Совокупность n линейно независимых векторов n - мерного векторного пространства (x, y) = (y, x), (α ·x, y) = α ·(x, y), (x + y, z) = (x, z) + (y, z), (x, x) > 0 при x ≠ 0, (0, 0) = 0, то в пространстве L определено скалярное произведение (x, y).
Вопрос 14 Прямая на плоскости: Общее уравнение Ax + By + C ( Вектор В векторном виде: Частные случаи: 1) By + C = 0 - прямая параллельна оси Ox; 2) Ax + C = 0 - прямая параллельна оси Oy; 3) Ax + By = 0 - прямая проходит через начало координат; 4) y = 0 - ось Ox; 5) x = 0 - ось Oy.
Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором этой прямой. Направляющий вектор произвольной прямой в дальнейшем обозначается буквой
Если известна одна точка
Каноническое уравнение прямой
Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М 1 и вектора Вектор Итак, пусть прямая l проходит через точку М 1(x 1, y 1, z 1), лежащую на прямой параллельно вектору Рассмотрим произвольную точку М(x,y,z) на прямой. Из рисунка видно, что Векторы Запишем это уравнение в координатной форме. Заметим, что Полученные уравнения называются параметрическими уравнениями прямой. При изменении параметра t изменяются координаты x, y и z и точка М перемещается по прямой.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 872; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.008 с.) |

 , то она линейно зависима.
, то она линейно зависима. векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.
векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных. линейно независима, а после присоединения к ней вектора
линейно независима, а после присоединения к ней вектора  оказывается линейно зависимой, то вектор
оказывается линейно зависимой, то вектор  — линейно зависима, то существуют числа
— линейно зависима, то существуют числа  , не все равные 0, что. В этом равенстве
, не все равные 0, что. В этом равенстве  . В самом деле, если
. В самом деле, если  , то
, то  . Значит, нетривиальная линейная комбинация векторов
. Значит, нетривиальная линейная комбинация векторов  , т.е. вектор
, т.е. вектор  и
и  , причем не все коэффициенты разложений соответственно равны между собой (например,
, причем не все коэффициенты разложений соответственно равны между собой (например,  ).
). получаем
получаем  .
. ), то эта комбинация нетривиальная, что противоречит условию линейной независимости векторов
), то эта комбинация нетривиальная, что противоречит условию линейной независимости векторов  называется n -мерным, если в нем можно найти n линейно независимых векторов, но больше, чем n линейно независимых векторов оно не содержит.
называется n -мерным, если в нем можно найти n линейно независимых векторов, но больше, чем n линейно независимых векторов оно не содержит.
 .
.
 неравенство
неравенство 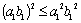 верно. Допустим,
верно. Допустим,
 .
Докажем, что
.
Докажем, что

 .
Перепишем это неравенство, частично раскрыв скобки:
.
Перепишем это неравенство, частично раскрыв скобки:


 .
Легко заметить, что для того, чтобы доказать это неравенство, достаточно доказать
.
Легко заметить, что для того, чтобы доказать это неравенство, достаточно доказать
 Перенеся все слагаемые в одну сторону, и сгруппировав их, получаем очевидное неравенство:
Перенеся все слагаемые в одну сторону, и сгруппировав их, получаем очевидное неравенство:
 А это и доказывает неравенство Коши-Буняковского.
А это и доказывает неравенство Коши-Буняковского.
 называется средним арифметическим чисел
называется средним арифметическим чисел 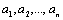 .
2. Если
.
2. Если  , то число
, то число  называется средним геометрическим чисел
называется средним геометрическим чисел 
 . (1)
. (1)
 . При m=1 надо доказать, что
. При m=1 надо доказать, что  . Это неравенство эквивалентно
. Это неравенство эквивалентно  , то есть
, то есть  . Последнее неравенство верно, значит, и первоначальное верно, так как они равносильны. Допустим, неравенство верно при m=k, то есть
. Последнее неравенство верно, значит, и первоначальное верно, так как они равносильны. Допустим, неравенство верно при m=k, то есть
 . (2)
Докажем неравенство (1) для m=k+1, то есть докажем, что
. (2)
Докажем неравенство (1) для m=k+1, то есть докажем, что
 .
В самом деле,
.
В самом деле, 


 .
Итак, мы доказали неравенство Коши, когда количество чисел в средних есть степень двойки. А как быть с остальными? Для них мы докажем неравенство Коши, используя еще одну модификацию индукции – "индукцию вниз". Допустим, что неравенство Коши верно для n=k, то есть допустим, что
.
Итак, мы доказали неравенство Коши, когда количество чисел в средних есть степень двойки. А как быть с остальными? Для них мы докажем неравенство Коши, используя еще одну модификацию индукции – "индукцию вниз". Допустим, что неравенство Коши верно для n=k, то есть допустим, что
 , (3)
и докажем это неравенство для n=k-1. Для этого в неравенстве Коши положим
, (3)
и докажем это неравенство для n=k-1. Для этого в неравенстве Коши положим  , тогда (3) будет иметь вид:
, тогда (3) будет иметь вид:
 После элементарных алгебраических преобразований получили:
После элементарных алгебраических преобразований получили:
 .
Сократим неравенство на второй множитель правой части:
.
Сократим неравенство на второй множитель правой части:
 .
И, наконец, возведем обе части неравенства в степень
.
И, наконец, возведем обе части неравенства в степень  :
:
 .
Неравенство Коши доказано полностью.
.
Неравенство Коши доказано полностью.
 > 0).
> 0). = (А; В) - нормальный вектор прямой.
= (А; В) - нормальный вектор прямой. + С = 0, где
+ С = 0, где  - радиус-вектор произвольной точки на прямой (рис. 4.11).
- радиус-вектор произвольной точки на прямой (рис. 4.11). , его координаты - буквами l, m, n:
, его координаты - буквами l, m, n: .
. прямой и направляющий вектор
прямой и направляющий вектор 

 ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ
ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ , параллельного этой прямой.
, параллельного этой прямой. .
. .
. и
и  коллинеарны, поэтому найдётся такое число t, что
коллинеарны, поэтому найдётся такое число t, что  , где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М 1 и М соответственно через
, где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М 1 и М соответственно через  и
и  , получаем
, получаем  . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М, лежащей на прямой.
. Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М, лежащей на прямой. ,
,  и
и  отсюда
отсюда 



