
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные регрессионные модели с переменной структурой. Фиктивные переменныеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
До сих пор мы рассматривали регрессионную модель, в которой в качестве объясняющих переменных выступали количественные переменные (производительность труда, себестоимость продукции, доход и т. п.). Однако на практике достаточно часто возникает необходимость исследования влияния качественных признаков, имеющих два или несколько уровней (градаций). К числу таких признаков можно отнести пол (мужской, женский), образование (начальное, среднее, высшее), фактор сезонности (зима, весна, лето, осень) и т. п. Например, нам надо изучить зависимость размера заработной платы работников Y не только от количественных факторов В принципе можно было бы получить оценки регрессионной модели
для каждого уровня качественного признака (т. е. выборочное уравнение регрессии отдельно для работников-мужчин и отдельно – для женщин), а затем изучать различия между ними. Но есть и другой подход, позволяющий оценивать влияние количественных переменных и уровней качественных признаков с помощью одного уравнения регрессии. Этот подход связан с введением так называемых фиктивных переменных. В качестве фиктивных переменных обычно используют дихотомические (булевы) переменные, которые принимают всего 2 значения: 0 или 1 (например, значение такой переменной Z1 по фактору «пол»: Z1=0 для работников-женщин и Z1=1 для мужчин). В этом случае первоначальная регрессионная модель (2.61) заработной платы изменится и примет вид
1, если i -й работник мужского пола; где 0, если i -й работник женского пола.
Таким образом, принимая модель (2.62), мы считаем, что средняя заработная плата у мужчин на Следует отметить, что в принципе качественное различие можно формализовать с помощью любой переменной, принимающей два разных значения, не обязательно 0 или 1. Однако в эконометрической практике почти всегда используются фиктивные переменные типа «0-1», так как при этом интерпретация полученных результатов выглядит наиболее просто. Если рассматриваемый качественный признак имеет несколько (k) уровней (градаций), то в принципе можно было бы ввести в регрессионную модель дискретную переменную, принимающую такое же количество значений (например, при исследовании зависимости заработной платы Y от уровня образования Z можно рассматривать k=3 значения: zi1=1 при наличии начального образования, zi1=2 – среднего и zi1=3 при наличии высшего образования). Однако обычно так не поступают из-за трудности содержательной интерпретации соответствующих коэффициентов регрессии, а вводят k-1 бинарных переменных. В рассматриваемом примере для учета факторов образования можно в регрессионную модель (2.62) ввести k-1=3-1=2 бинарные переменные Z1 и Z2:
1, если i- й работник имеет высшее образование; где 0 во всех остальных случаях.
0 во всех остальных случаях.
Третьей бинарной переменной очевидно не требуется, если i- й работник имеет начальное образование, это будет отражено парой значений
Это означает линейную зависимость столбцов общей матрицы X, т. е. мы оказались бы в условиях мультиколлинеарности в функциональной форме и как следствие – невозможности получения оценок методом наименьших квадратов. Пример. Необходимо исследовать зависимость между результатами письменных вступительных и курсовых экзаменов по математике. Получены следующие данные о числе решенных задач на вступительных экзаменах X (задание – 10 задач) и курсовых экзаменах Y (задание – 7 задач) 12 студентов, а также распределение этих студентов по фактору «пол».
Построим линейную регрессионную модель Y по X с использованием фиктивной переменной по фактору «пол». Для ее учета введем в регрессионную модель фиктивную бинарную переменную Z.
1, если i -й студент мужского пола; zi = 0, если i -й студент женского пола.
Таким образом, мы получили регрессионную модель
с общей матрицей
│1 1 1 1 1 1 1 1 1 1 1 1 │ ХT = │10 6 8 8 6 7 6 7 9 6 5 7 │ │1 0 1 0 0 1 0 1 1 0 1 0 │
По формуле (2.45) найдем вектор оценок параметров регрессии
Таким образом, выборочное уравнение множественной регрессии примет вид
Коэффициент детерминации Уравнение регрессии значимо по F -критерию при 5%-м уровне значимости, так как в соответствии с (2.55)
Из (2.64) следует, что при том же числе решенных задач на вступительных экзаменах Х, на курсовых экзаменах юноши решают в среднем на 0,466 ≈ 0,5 задачи больше. Полученное уравнение множественной регрессии значимо по
Следовательно, по имеющимся данным влияние фактора «пол» оказалось несущественным, и у нас есть основание считать, что регрессионная модель результатов курсовых экзаменов по математике в зависимости от вступительных одна и та же для юношей и девушек.
Нелинейные модели регрессии
До сих пор мы рассматривали линейные регрессионные модели, в которых переменные имели первую степень (модели, линейные по переменным), а параметры выступали в виде коэффициентов при этих переменных (модели, линейные по параметрам). Однако соотношения между экономическими переменными далеко не всегда можно выразить линейными функциями. Так, например, нелинейными оказываются производственные функции (зависимости между объемом произведенной продукции и основными факторами производства – трудом и капиталом). Для оценки параметров нелинейных моделей используются два подхода. Первый подход основан на линеаризации модели и заключается в том, что с помощью подходящих преобразований исходных переменных исследуемую зависимость представляют в виде линейного соотношения между преобразованными переменными. Второй подход применяется в случае, когда подобрать соответствующее линеаризующее преобразование не удается. В этом случае применяются методы нелинейной оптимизации на основе исходных переменных. Для линеаризации модели в рамках первого подхода могут использоваться как модели, не линейные по переменным, так и не линейные по параметрам. Если модель нелинейна по переменным, то введением новых переменных ее можно свести к линейной модели, для оценки параметров которой использовать обычный метод наименьших квадратов. Так, например, если необходимо оценить параметры регрессионной модели
то, вводя новые переменные
параметры которой находятся обычным методом наименьших квадратов. Более сложной проблемой является нелинейность модели по параметрам, так как непосредственное применение метода наименьших квадратов для их оценивания невозможно. К числу таких моделей можно отнести, например, мультипликативную модель
экспоненциальную модель
и другие. В ряде случаев путем подходящих преобразований эти модели удается привести к линейной форме. Так, модели (2.65) и (2.66) могут быть приведены к линейным логарифмированием обеих частей уравнений. Тогда, например, модель (2.65) примет вид
К модели (2.67) уже можно применять обычные методы исследования линейной регрессии. Следует однако отметить и недостаток такой замены, связанный с тем, что вектор оценок Заметим попутно, что к модели
изложенные методы уже непригодны, так как модель (2.68) нельзя привести к линейному виду. В качестве примера использования линеаризирующего преобразования регрессии рассмотрим производственную функцию Кобба – Дугласа
где Учитывая влияние случайных возмущений, присущих каждому экономическому явлению, функцию Кобба–Дугласа (2.69) можно представить в виде
Полученную мультипликативную модель легко свести к линейной путем логарифмирования обеих частей уравнения (2.70). Тогда для i -го наблюдения получим
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 806; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.72.24 (0.011 с.) |

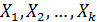 , но и от качественного признака
, но и от качественного признака  , например фактора «пол работника».
, например фактора «пол работника».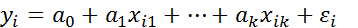 (i=1,..,n) (2.61)
(i=1,..,n) (2.61) (i=1,..,n) (2.62)
(i=1,..,n) (2.62)
 =
= *1 =
*1 =  , (2.63)
, (2.63)
 1, если i- й работник имеет среднее образование;
1, если i- й работник имеет среднее образование; =
= = 0,
= 0,  = 0. Более того, вводить третью бинарную переменную Z3 со значениями
= 0. Более того, вводить третью бинарную переменную Z3 со значениями 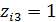 , если i- й работник имеет начальное образование;
, если i- й работник имеет начальное образование;  - в остальных случаях, нельзя, так как при этом для любого i- го работника
- в остальных случаях, нельзя, так как при этом для любого i- го работника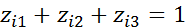 .
.

 .
. . (2.64)
. (2.64) .
. .
. – критерию. Однако коэффициент регрессии β1 при фиктивной переменной Z незначим по t - критерию
– критерию. Однако коэффициент регрессии β1 при фиктивной переменной Z незначим по t - критерию .
. (i=1,…,n),
(i=1,…,n), , получим линейную модель
, получим линейную модель (i=1,…,n),
(i=1,…,n), (i=1,..,n), (2.65)
(i=1,..,n), (2.65) (i=1,..,n) (2.66)
(i=1,..,n) (2.66) (i=1,..,n). (2.67)
(i=1,..,n). (2.67)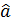 получается не из условия минимизации суммы квадратов отклонений для исходных переменных, а из условия минимизации суммы квадратов отклонений для преобразованных переменных, что не одно и то же. Следует также подчеркнуть, что критерии значимости и интервальные оценки параметров, применимые для нормальной линейной регрессии, требуют, чтобы нормальный закон распределения в моделях (2.65), (2.66) имел логарифм вектора возмущений
получается не из условия минимизации суммы квадратов отклонений для исходных переменных, а из условия минимизации суммы квадратов отклонений для преобразованных переменных, что не одно и то же. Следует также подчеркнуть, что критерии значимости и интервальные оценки параметров, применимые для нормальной линейной регрессии, требуют, чтобы нормальный закон распределения в моделях (2.65), (2.66) имел логарифм вектора возмущений  а вовсе не ε.
а вовсе не ε. (i=1,..,n) (2.68)
(i=1,..,n) (2.68) , (2.69)
, (2.69) – объем производства;
– объем производства; 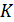 – затраты капитала;
– затраты капитала;  – затраты труда.
– затраты труда. . (2.70)
. (2.70) =
=  +
+  (i=1,..,n). (2.71)
(i=1,..,n). (2.71)


