
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распространение электромагнитной волны в нелинейной средеСодержание книги
Поиск на нашем сайте
§ 8. ОБЩИЕ ПРЕДСТАВЛЕНИЯ О НЕЛИНЕЙНОМ ОТКЛИКЕ СРЕДЫ
Распространение электромагнитных волн в веществе сопровождается наведением в последней зарядов и токов, которые в сравнительно небольших полях прямо пропорциональны величине внешнего воздействия. Электродинамика волнового движения в этом случае линейная и полностью определяется диэлектрической проницаемостью вещества. Волны не взаимодействуют друг с другом, они независимы, то есть справедлив принцип суперпозиции. Однако по мере увеличения интенсивности наведенные заряды и токи уже не являются линейными функциями внешних полей, а начинают сложным образом зависеть не только от электромагнитного поля, но и от других волновых процессов в веществе (от звуковых колебаний, спиновых волн и т.п.). Вследствие этого распространение электромагнитной волны приобретает нелинейный характер и нарушает принцип суперпозиции. Процессы, лежащие в основе нелинейности, весьма разнообразны и зависят как от параметров внешних полей, так и от состава и фазового состояния вещества. Одним из наиболее важных процессов является процесс нагрева вещества в электрическом поле волны. В твердых телах поглощение электромагнитной энергии происходит путем одноквантового или многоквантового процесса возбуждения электронов или фононов. Поглощенная энергия в конечном счете переходит в акустические и оптические колебания твердого тела, и, как следствие, происходит разогрев среды, ее тепловое расширение, что приводит к изменению диэлектрической проницаемости вещества. Этот процесс нелинейности называют тепловым или нагревным. Особенно легко этот тип нелинейности осуществляется в плазме при малых электрических полях. Действительно, когда длина свободного пробега электронов сравнительно большая, так что электрон за время одного пробега может получить заметную долю энергии, а передача энергии от электронов к ионам, атомам и молекулам затруднена из-за большой разницы в массах, то электроны сильно разогреваются уже в малом по величине поле. Такой же тип нелинейности может быть на горячих электронах в полупроводниках и диэлектриках, в плазме твердого тела. С ростом амплитуды электрического поля электроны набирают энергию, достаточную для ударной ионизации. Это приводит к лавинному нарастанию плотности электронов, и, по-существу, возникает новый тип нелинейности, связанный с фазовым переходом диэлектрик-металл в веществе. Другой очень распространенный тип нелинейности связан с воздействием электрических (пондеромоторных) сил в среде в произвольном неоднородном электромагнитном поле. Эти силы оказывают давление на вещество, производят его сжатие или разрежение, изменяют его плотность и, как следствие, диэлектрическую проницаемость. Такой механизм нелинейности называют стрикционным. Этот тип нелинейности становится важным для относительно коротких импульсов излучения, например, меньших времени свободного пробега электрона, то есть когда нагревныи механизм дает малый вклад. Стрикционный механизм нелинейности играет важную роль при параметрической неустойчивости вещества, приводит к усилению звуковых волн, к процессам вынужденного рассеяния на акустических колебаниях среды, к возбуждению собственных колебаний плазмы и другим эффектам. Наблюдаются и другие процессы нелинейности. Например, ориентационный механизм, характерный для жидкостей, состоящих из анизотропных молекул. Молекулярная поляризуемость таких молекул анизотропна. Это заставляет такие молекулы ориентироваться во внешнем линейно поляризованном электромагнитном поле таким образом, чтобы ось наибольшей поляризуемости молекулы совпадала с направлением поляризации внешнего поля. В плазме возможен магнитный тип нелинейности, когда под действием электрического поля волны электрон приобретает переменную скорость, а магнитное поле изменяет это движение электрона посредством силы Лоренца. Для очень коротких световых импульсов основными механизмами нелинейности становятся такие малоинерционные процессы, как эффект электронной поляризуемости или эффект молекулярной либрации (качание молекул в поле световой волны). Наконец, особое значение имеют резонансные механизмы нелинейности, когда частота волны (или ее гармоники и субгармоники) достаточно близка к собственным частотам колебаний вещества (к частотам атомных переходов в атомах или молекулах, к ширине запрещенной зоны в полупроводниках и диэлектриках, к частоте плазменных колебаний и т.д.). В резонансных условиях нелинейности резко возрастают, и соответствующие нелинейные эффекты развиваются при меньших полях, чем в нерезонансном случае. Все перечисленные механизмы нелинейности приводят к возмущению комплексной диэлектрической проницаемости вещества. Для изотропной среды и в относительно слабых внешних электрических полях такая зависимость может быть записана в виде
где Рассмотрим качественно основные явления, которые могут возникнуть вследствие того или иного процесса нелинейности при распространении в среде мощной электромагнитной волны. Прежде всего меняется характер поглощения электромагнитных волн, который существенно зависит от знака мнимой части нелинейного коэффициента Такой процесс поглощения имеет место при прохождении сильной световой волны через диэлектрик или собственный полупроводник в случае, когда возможны прямые переходы из валентной зоны в зону проводимости в результате поглощения одного или нескольких фотонов. В зоне проводимости быстро возрастает плотность электронов (а в валентной зоне - плотность дырок), на которых возникает дополнительный процесс поглощения. В противоположном случае (при В сильных полях изменяется не только коэффициент поглощения, но и показатель преломления - действительная часть диэлектрической проницаемости. В результате возникает ряд новых нелинейных эффектов, в частности, искажается траектория луча. Если знак нелинейного коэффициента Дляочень узких пучков существенной становится дифракционная расходимость, которая начинает конкурировать с самофокусировкой. В результате может произойти самозахват электромагнитных волн в узкие волноводы - каналы, то есть произойдет явление самоканализации волны. Импульс света, распространяющийся в нелинейной среде, сильно искажает свою форму, происходит самосжатие и самоукручение импульса. Аналогичные процессы характерны не только для изменения амплитуды поля, но и его частоты. Это явление получило название фазовой самомодуляциии. Мощные световые поля способны вызвать значительные изменения в состоянии вещества, исказить его структуру, что в еще большей степени усиливает нелинейные эффекты. Распространение плоской волны становится неустойчивым: она может распадаться и расслаиваться на отдельные пучки и импульсы.
§ 9. НЕЛИНЕЙНАЯ ГЕОМЕТРИЧЕСКАЯ ОПТИКА
В нелинейном изотропном диэлектрике без поглощения плоская световая волна имеет постоянное направление распространения и амплитуду в каждой точке пространства и описывается известным выражением
Волновой вектор
где диэлектрическая проницаемость Произвольные световые волны этими свойствами не обладают. Однако некоторые волны на каждом небольшом участке пространства и в малом интервале времени можно рассматривать как плоские и монохроматические. Если электрическое поле в такой световой волне записать в виде
то, очевидно, необходимо соблюсти условие, при котором амплитуда На малых участках пространства и в малых интервалах времени фаза
Введем определение волнового вектора и частоты плоской волны в точке
в соответствии с фазой плоской монохроматической волны (9.1). В световой волне дисперсионное уравнение (9.2) можно рассматривать как функцию частоты от волнового вектора и амплитуды поля
Если подставить в (9.6) выражения (9.4) и (9.5), то получим основное уравнение нелинейной геометрической оптики, конкретный вид которого определяется диэлектрической проницаемостью. Например, в среде без пространственной и частотной дисперсии уравнение для фазы
где фазовая скорость Между геометрической оптикой и механикой материальной частицы существует известная аналогия. Умножим уравнения (9.4) и (9.5) на постоянную Планка
Первое из них есть определение импульса частицы через функцию действия
эквивалентные уравнению Гамильтона-Якоби. Следовательно, для лучей световых волн можно написать аналогичные уравнения
В линейной оптике в однородной изотропной среде лучи распространяются по прямым линиям, при этом частота остается постоянной вдоль траектории луча. В нелинейной оптике это уже не наблюдается, поскольку частота зависит от амплитуды внешнего поля согласно (9.6), и, следовательно, искривление лучей в пространстве обусловлено распределением интенсивности света. Существенно то, что в нелинейной оптике на фазу волны влияет амплитуда поля. В прозрачной среде для описания изменения амплитуды
Это уравнение непрерывности для плотности электромагнитной энергии. Таким образом, уравнение для эйконала (9.7) и уравнение (9.10) совместно определяют ход лучей в нелинейной оптике. Теперь рассмотрим распространение в пространстве импульса света в виде волнового пакета, близкого к плоской монохроматической волне с волновым вектором
где
где
Представим в последнем уравнении частоту
Применим изложенную выше методику к исследованию волновых пакетов, фаза и амплитуда которых зависит от координаты
в котором оставлены первые три члена ряда (9.11) и введено обозначение для групповой скорости
При выводе этого уравнения использовано представление скорости
где Далее перейдем к рассмотрению новых переменных
и новых обозначений
В результате вместо (9.16) и (9.17) получим уравнения
где Система уравнений (9.19, 9.20) аналогична уравнениям одномерной гидрогазодинамики [3].Уравнение (9.19) эквивалентно уравнению Эйлера, где
В адиабатическом процессе
Таким образом, уравнения (9.19) и (9.20) соответствуют уравнениям гидродинамики с
§ 10. НЕЛИНЕЙНОЕ ПАРАБОЛИЧЕСКОЕ УРАВНЕНИЕ . Распространение плоских волн и волновых пакетов, близких к плоских волнам, можно описывать параболическим уравнением, вывод которого дается в этом параграфе. Сначала рассмотрим вывод, характеризующей однородную линейную диспергирующую среду, затем обобщим результаты на случай рассмотрения неоднородной среды и далее нелинейной среды в нелинейной оптике. Предположим, что электромагнитное поле распространяется в изотропном немагнитном диэлектрике. Электрическое поле волны удовлетворяет уравнению Максвелла(6.6).Для определения фурье-компоненты электрического поля и индукции удобно ввести следующие выражения:
В изотропной диспергирующнй линейной среде связь между фулье-компонентами поля и индукции представлена в виде
где постоянная
Поскольку
которое определяет функцию Предположим, что фурье-компонента
и перепишем (10.3) в виде
откуда следует, что
Функцию
где Рассмотрим значение
тогда
где
и ее производную
Подставим (10.7) в (10.6) и ограничимся членами второго порядка малости. Тогда уравнение (10.5) примет вид
Далее выполним обратное фурье-преобразование
И в результате придем к линейному параболическому уравнению:
Здесь Обобщим полученное уравнение для неоднородной среды. Часто неоднородную среду можно описать электрической проницаемостью, зависящей от координаты
где
где первое слагаемое описывает поле в однородной среде с диэлектрической постоянной
Как видно из (10.8), получение параболический уравнений (10.9) и (10.11) с помощью фурье-преобразований сводится к заменам
Предположим, что световая волна линейно поляризована, тогда из (10.11) видно, что поляризация сохраняется при движении волны в среде. Поэтому выберем ось вдоль поляризации и будем рассматривать лишь величины поля. Далее в уравнении (10.10) перейдем к новой переменной
В этом случае (10.10) преобразуется в уравнение
в которое введены обозначения
Полученное уравнение есть уравнение Шредингера для описания частицы в потенциальном поле. Частица имеет различные массы (эффективный тензор масс) в зависимости от направления. Такие квазичастицы изучаются в разделе физики твердого тела и физики полупроводников для описания носителей тока в кристаллической решетке, экситонных и примесных состояний. Таким образом, амплитуда волнового пакета в неоднородной среде и волновая функция для частицы в потенциальном поле в квантовой механике аналогичны. Теперь нетрудно перейти к случаю нелинейных сред, когда диэлектрическая проницаемость зависит от электрического поля волны. Поскольку огибающая волнового пакета является функцией координат и времени, то нелинейная среда будет неоднородной. Поэтому в нелинейной среде параболическое уравнение примет тот же вид (10.11) или (10.12), где вместо
Если воспользоваться обозначениями (10.13), то (10.14) можно представить в виде
где
§ 11. УСТОЙЧИВОСТЬ ПЛОСКОЙ ВОЛНЫ В НЕЛИНЕЙНОЙ СРЕДЕ
Запишем нелинейное параболическое уравнение более компактно:
В уравнении (11.1) ввели обозначение оператора
Поле волны представим в виде
Подставим выражение (11.2) в исходное уравнение (11.1) и разделяя мнимые и действительные части, получим
Отметим, что если пренебречь вторыми производными в (11.3) и (11.4), то придем к приближению геометрической оптики, причем для одномерного случая ( Если
Таким образом, при фиксированной амплитуде
Этот эффект можно наблюдать в кольцевом лазере бегущей волны. Исследуем устойчивость полученного решения. Предположим, что амплитуда и фаза волны имеют малые возмущения, то есть
Подставим эти выражения в уравнения (11.3) и (11.4) и удержим лишь величины первого порядка по малым возмущениям (то есть проведем линеаризацию уравнений), в результате получим систему
Делая вывод, мы использовали явный вид оператора
Подставляя (11.6) в (11.5), получим дисперсионное уравнение
где
Из (11.7) находим, что
Проведем анализ полученного результата для некоторых частных случаев. Пусть
корень в (11.9) становится чисто мнимым. Иными словами, плоская волна становится неустойчивой в поперечном направлении. Знак равенства при этом соответствует порогу самозахвата плоской волны, а дифракционная расходимость подавляется самофокусировкой. Если размер пучка
Видно, что пороговая мощность не зависит от размеров поперечного пучка. Рассмотрим плоскую волну, устойчивую в поперечном направлении
Если
корень становится мнимым, то есть волна неустойчива для продольных возмущений. В отдельных местах она будет “расползаться”, а в других – “сгущаться”. Этот эффект носит пороговый характер, аналогичный эффекту самофокусировки, при условии, конечно, что нелинейный коэффициент
И волна становится неустойчивой при
Которое заведомо выполнялось в предыдущем случае, но так же и при
Рис.4. Разбиение монохроматической волны на отдельные волновые “пакеты” (начальная стадия)
Физика неустойчивости в данном случае следующая: плоская волна, движущаяся в некотором направлении (рис.4), промодулирована по амплитуде в этом же направлении. В точках a (“горбы”) амплитуда поля больше, чем в точках b (“впадины”). Поэтому фазовая скорость на “горбах” больше (при Так как
§ 12. СОЛИТОНЫ
Как показано в предыдущем параграфе, при определенных условиях плоская волна становится неустойчивой относительно продольных возмущений. Волна разбивается на отдельные волновые пакеты, которые изменяют свою форму, в частности, испытывают самосжатие. Однако для сильно сжатого волнового пакета существенную роль начинает играть дисперсионное расплывание пакета, имеющее место в обычной линейной оптике. Конкуренция самосжатия и дисперсионного расплывания может привести к стабилизации формы волнового пакета. Возникает устойчивый импульс, который двигается в среде, не изменяя своей формы. Такую уединенную волну называют солитоном. Рассмотрим подробнее формирование такого устойчивого волнового пакета в нелинейной среде. Будем искать амплитуду волнового пакета в виде
В данном случае полагаем, что волна стабилизирована в поперечном направлении и обладает огибающей амплитуды в продольном направлении, нахождение формы которой и является нашей задачей. Подставим (12.1) в нелинейное параболическое уравнение (11.1) и получим
Упростим это уравнение. Введем новую переменную
И перепишем (12.2) в иной форме, а именно:
где представляет собой уравнение Ньютона для материальной точки единичной массы в потенциальном поле вида (12.4) (рис.5). Из графиков видно, что имеется два минимума при
Рис.5. “Потенциальная энергия” образования устойчивых форм волнового “пакета” в нелинейной среде
Откуда видно, что частота гармон
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 561; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.1.100 (0.016 с.) |

 (8.1)
(8.1) - амплитуда внешнего поля электромагнитной волны. Таким образом, в веществе показатель преломления и коэффициент поглощения становятся квадратичными функциями амплитуды поля, что приводит к целому ряду нелинейных оптических эффектов.
- амплитуда внешнего поля электромагнитной волны. Таким образом, в веществе показатель преломления и коэффициент поглощения становятся квадратичными функциями амплитуды поля, что приводит к целому ряду нелинейных оптических эффектов. в формуле для диэлектрической проницаемости. (8.1). При
в формуле для диэлектрической проницаемости. (8.1). При  величина поглощения возрастает с увеличением мощности поля. В целом это приводит к тому, что сильная волна, проникающая в такую нелинейную среду, не может превзойти определенного предела. Поле внутри среды перестает зависеть от величины падающей извне мощности излучения, и происходит как бы насыщение поля в глубине среды.
величина поглощения возрастает с увеличением мощности поля. В целом это приводит к тому, что сильная волна, проникающая в такую нелинейную среду, не может превзойти определенного предела. Поле внутри среды перестает зависеть от величины падающей извне мощности излучения, и происходит как бы насыщение поля в глубине среды. ) поглощение уменьшается с ростом мощности поля, и в предельном случае сильная волна проходит через среду без поглощения, возникает просветление среды. Этот процесс часто протекает в условиях резонансного поглощения, когда происходит насыщение населенностей на резонансных уровнях. Оба рассмотренных механизма нелинейного поглощения могут осуществляться в одном и том же веществе при различных его состояниях. Например, в плазме разогрев электронов в поле мощной электромагнитной волны приводит к изменению частоты столкновений электронов с ионами, нейтральными атомами и молекулами. Если основную роль играют столкновения с нейтральными частицами, то с ростом температуры частота соударений возрастает и, следовательно, увеличивается поглощение. Если главными становятся столкновения электронов с ионами, то частота соударений падает с ростом температуры, и степень поглощения уменьшается. Таким образом, при переходе от слабоионизированной плазмы к сильноионизированной характер нелинейного поглощения меняется на противоположный.
) поглощение уменьшается с ростом мощности поля, и в предельном случае сильная волна проходит через среду без поглощения, возникает просветление среды. Этот процесс часто протекает в условиях резонансного поглощения, когда происходит насыщение населенностей на резонансных уровнях. Оба рассмотренных механизма нелинейного поглощения могут осуществляться в одном и том же веществе при различных его состояниях. Например, в плазме разогрев электронов в поле мощной электромагнитной волны приводит к изменению частоты столкновений электронов с ионами, нейтральными атомами и молекулами. Если основную роль играют столкновения с нейтральными частицами, то с ростом температуры частота соударений возрастает и, следовательно, увеличивается поглощение. Если главными становятся столкновения электронов с ионами, то частота соударений падает с ростом температуры, и степень поглощения уменьшается. Таким образом, при переходе от слабоионизированной плазмы к сильноионизированной характер нелинейного поглощения меняется на противоположный.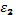 положителен, то луч отклоняется в сторону наибольшей интенсивности поля. В этом случав пучок лучей будет фокусироваться, а само явленно называют самофокусировкой. Если знак нелинейного коэффициента
положителен, то луч отклоняется в сторону наибольшей интенсивности поля. В этом случав пучок лучей будет фокусироваться, а само явленно называют самофокусировкой. Если знак нелинейного коэффициента  (9.1)
(9.1) и частота
и частота  связаны между собой дисперсионным уравнением
связаны между собой дисперсионным уравнением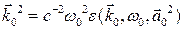 , (9.2)
, (9.2) зависит от амплитуды
зависит от амплитуды  .
. (9.3)
(9.3) и фаза
и фаза  как функции координат и времени почти не изменялись бы на расстояниях порядка длины волны и в интервалах времени порядка периода колебаний света. Изучение законов распространения света в таких условиях составляет предмет нелинейной геометрической оптики.
как функции координат и времени почти не изменялись бы на расстояниях порядка длины волны и в интервалах времени порядка периода колебаний света. Изучение законов распространения света в таких условиях составляет предмет нелинейной геометрической оптики. .
. и момент
и момент  по формулам
по формулам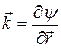 ; (9.4)
; (9.4) . (9.5)
. (9.5) . (9.6)
. (9.6) , (9.7)
, (9.7) зависит от квадрата амплитуды поля
зависит от квадрата амплитуды поля 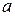 и, следовательно, есть функция координат и времени. Для сред, в которых важную роль начинают играть эффекты запаздывания (частотная дисперсия) или явления пространственной дисперсии, уравнение (9.7) значительно усложняется.
и, следовательно, есть функция координат и времени. Для сред, в которых важную роль начинают играть эффекты запаздывания (частотная дисперсия) или явления пространственной дисперсии, уравнение (9.7) значительно усложняется. и перепишем их в иной форме, введя обозначения
и перепишем их в иной форме, введя обозначения 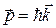 ,
,  ,
,  :
: ;
;  .
.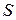 , а второе уравнение Гамильтона-Якоби. Для нахождения траектории частицы часто используются также уравнения Гамильтона
, а второе уравнение Гамильтона-Якоби. Для нахождения траектории частицы часто используются также уравнения Гамильтона ;
;  ,
, ; (9.8)
; (9.8) . (9.9)
. (9.9) . (9.10)
. (9.10) , (9.11)
, (9.11) - групповая скорость. Переопределим фазу
- групповая скорость. Переопределим фазу  , (9.12)
, (9.12) . Для новой фазы
. Для новой фазы  уравнения (9.5) и (9.6) принимают вид
уравнения (9.5) и (9.6) принимают вид ; (9.13)
; (9.13) . (9.14)
. (9.14) как ряд (9.11) по степеням
как ряд (9.11) по степеням  , вместо которых подставим уравнение (9.13). В результате получим уравнение для фазы, которое в данном случае эквивалентно уравнению для эйконала
, вместо которых подставим уравнение (9.13). В результате получим уравнение для фазы, которое в данном случае эквивалентно уравнению для эйконала . (9.15)
. (9.15)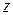 (одномерный случай). При этом уравнение (9.15) будет иметь вид
(одномерный случай). При этом уравнение (9.15) будет иметь вид , (9.16)
, (9.16) . Уравнение (9.10) в этом приближении запишем следующим образом:
. Уравнение (9.10) в этом приближении запишем следующим образом: . (9.17)
. (9.17) , (9.18)
, (9.18) , и произведена замена
, и произведена замена  на
на  .
. ;
; 
 ;
; 
 ; (9.19)
; (9.19) , (9.20)
, (9.20) .
. - скорость газа. Уравнение (9.20) есть уравнение непрерывности для плотности газа
- скорость газа. Уравнение (9.20) есть уравнение непрерывности для плотности газа  . Последний член уравнения (9.19) можно сопоставить с силой давления в гидродинамике
. Последний член уравнения (9.19) можно сопоставить с силой давления в гидродинамике .
. , где
, где  – скорость звука;
– скорость звука;  - равновесная плотность газа. В нелинейной геометрической оптике
- равновесная плотность газа. В нелинейной геометрической оптике
 . Как и в гидродинамике, в нелинейной оптике имеют место аналогичные явления укручения огибающей волнового пакета и формирования ударной волны.
. Как и в гидродинамике, в нелинейной оптике имеют место аналогичные явления укручения огибающей волнового пакета и формирования ударной волны. (10.1)
(10.1)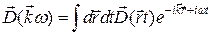
 , (10.2)
, (10.2) обозначает диэлектрическую проницаемость, зависящую от волнового вектора и частоты. Из уравнения Максвелла (6.6) и из выражений (10.1) с учетом уравнения
обозначает диэлектрическую проницаемость, зависящую от волнового вектора и частоты. Из уравнения Максвелла (6.6) и из выражений (10.1) с учетом уравнения  легко получаем
легко получаем . (10.3)
. (10.3) , то из (10.3) следует хорошо известное дисперсионное уравнение
, то из (10.3) следует хорошо известное дисперсионное уравнение ,
, , причем для изотропной среды частота зависит от величины волнового вектора, а не от его направления:
, причем для изотропной среды частота зависит от величины волнового вектора, а не от его направления:  . Фиксированному значению
. Фиксированному значению 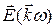 отлична от нуля в окрестности точки
отлична от нуля в окрестности точки  , то есть волновой пакет, близкий к плоской волне с заданными параметрами. Введем обозначение
, то есть волновой пакет, близкий к плоской волне с заданными параметрами. Введем обозначение
 , (10.4)
, (10.4) . (10.5)
. (10.5) представим как ряд
представим как ряд , (10.6)
, (10.6) , а индекс ноль у производных означает, что они берутся в той же точке.
, а индекс ноль у производных означает, что они берутся в той же точке. , близкое к
, близкое к 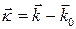
 , (10.7)
, (10.7) - проекция вектора
- проекция вектора  на направление вектора
на направление вектора  - проекция
- проекция 
 .
. .
. (10.8)
(10.8)
 . (10.9)
. (10.9) представляет собой медленно меняющуюся амплитуду плоской монохроматической волны с частотой
представляет собой медленно меняющуюся амплитуду плоской монохроматической волны с частотой  ; ось
; ось  ,
, - некоторое среднее значение диэлектрической постоянной. Тогда вместо (10.5) будем иметь
- некоторое среднее значение диэлектрической постоянной. Тогда вместо (10.5) будем иметь , (10.10)
, (10.10) . Обратное Фурье-преобразование приводит нас к уравнению
. Обратное Фурье-преобразование приводит нас к уравнению . (10.11)
. (10.11) ,
,  ,
,  .
. .
. , (10.12)
, (10.12) ;
;  ;
;  ;
;  . (10.13)
. (10.13) необходимо иметь
необходимо иметь 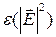 . Например, для слаболинейной среды зависимость диэлектрической проницаемости от поля представлена как в (8.1), и поэтому нелинейное параболическое уравнение принимает форму:
. Например, для слаболинейной среды зависимость диэлектрической проницаемости от поля представлена как в (8.1), и поэтому нелинейное параболическое уравнение принимает форму: . (10.14)
. (10.14) , (10.15)
, (10.15) . В стационарном случае последнее уравнение совпадает с уравнением Гинзбурга-Ландау в феноменологической теории сверхпроводимости [12].
. В стационарном случае последнее уравнение совпадает с уравнением Гинзбурга-Ландау в феноменологической теории сверхпроводимости [12]. . (11.1)
. (11.1)
 . (11.2)
. (11.2) ; (11.3)
; (11.3) . (11.4)
. (11.4) ) эти уравнения совпадают с (9.16) при определении фазы с точностью до постоянной величины.
) эти уравнения совпадают с (9.16) при определении фазы с точностью до постоянной величины. ,
,  - лишь функция времени, то из (11.4) следует, что
- лишь функция времени, то из (11.4) следует, что .
. и волновом векторе
и волновом векторе  частота плоской волны сдвигается и становится равной
частота плоской волны сдвигается и становится равной .
. ,
, 
 ,
, 
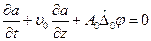 ; (10.5)
; (10.5) .
. . Решение системы (11.5) представим в виде
. Решение системы (11.5) представим в виде ; (11.6)
; (11.6) .
. (11.7)
(11.7) определяется соотношением
определяется соотношением . (11.8)
. (11.8) . (11.9)
. (11.9) , что означает отсутствие продольных (вдоль направления распространения волны) возмущений. Тогда из (11.8) и (11.9) видно, что при условии
, что означает отсутствие продольных (вдоль направления распространения волны) возмущений. Тогда из (11.8) и (11.9) видно, что при условии
 , то наименьшее
, то наименьшее 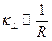 , поэтому пороговую мощность самозахвата можно оценить согласно выражению
, поэтому пороговую мощность самозахвата можно оценить согласно выражению .
. . Из (11.8) следует, что
. Из (11.8) следует, что .
. , то при условии
, то при условии (11.10)
(11.10) . Для малых
. Для малых  неравенство (11.10) выполняется со значительным запасом. Более того, в этом случае имеем
неравенство (11.10) выполняется со значительным запасом. Более того, в этом случае имеем
 ,
, и
и  .
.
 . (12.1)
. (12.1) . (12.2)
. (12.2) ,
, ; (12.3)
; (12.3) , (12.4)
, (12.4) . Уравнение (12.3)
. Уравнение (12.3) . Это означает, что плоская волна с такой амплитудой будет устойчива. Потенциальная энергия вблизи своего минимума имеет вид
. Это означает, что плоская волна с такой амплитудой будет устойчива. Потенциальная энергия вблизи своего минимума имеет вид .
.



