
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классическое и квантовое описание оптического поляСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Глава I Глава II
Глава III
Нелинейные восприимчивости §14. НЕЛИНЕЙНАЯ СВЯЗЬ МЕЖДУ ПОЛЯРИЗАЦИЕЙ И ЭЛЕКТРИЧЕСКИМ ПОЛЕМ
Средний (макроскопический) дипольный момент единицы объема вещества (поляризация) определяет многие электродинамические (в том числе и оптические) свойства среды. В немагнитных диэлектриках поляризация вещества
Первое слагаемое описывает линейные свойства вещества, а
Слагаемые В переменном электрическом поле, в том числе и в световой волне, существенным становится эффект запаздывания: поляризация в определенный момент времени зависит не только от электрического поля в этот же момент, но и от полей в предыдущие моменты времени. Следовательно, поляризация
то есть точно такую же зависимость, как и в статическом поле, с той лишь разницей, что линейная восприимчивость теперь является функцией частоты
Для того чтобы определить поляризацию от всех монохроматических волн в определенный момент времени, достаточно составить сумму
где суммирование ведется по положительным и отрицательным частотам волн, распространяющихся в веществе. Для волнового “пакета”
и в этом случае в (14.4) необходимо суммирование заменить соответствующим интегрированием, а именно:
По мере увеличения амплитуды электрического поля становится важным взаимодействие волн друг с другом, и принцип суперпозиции оптики нарушается. Вид нелинейной зависимости (14.1) подсказывает, что наведенная в среде нелинейная поляризация при распространении двух волн с частотами
В данном случае волна поляризации возникает на частоте
где суммирование ведется по всем положительным и отрицательным частотам. Для волновых “пакетов” сумму надо заменить на соответствующий интеграл. С квантово-механической точки зрения, такой процесс взаимодействия означает “уничтожение” двух квантов Аналогично (14.6) определяют нелинейную восприимчивость третьего порядка
и последующих – четвертого, пятого и т.д. До сих пор мы предполагали (для простоты анализа), что направления полей и поляризации одинаковы, и учет их в анизотропных средах становится весьма существенным. В этом случае каждая из величин
Число отличных от нуля компонент тензоров
§15. КЛАССИФИКАЦИЯ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ЭФФЕКТОВ
Изучая общие свойства нелинейных восприимчивостей, изложенные в предыдущем параграфе, можно сделать ряд заключений. Именно из (14.7) и (14.8) следует, что
Аналогичные соотношения имеют место для нелинейной восприимчивости Из определений (14.7) и (14.8) видно, какие нелинейные восприимчивости “ответственны” за тот или иной нелинейно-оптический эффект. Действительно, Здесь уместно остановиться еще на одном свойстве тензора
Это выражение можно записать в виде
откуда следует, что все компоненты
Эта ситуация аналогична консервативным силам в механике. В результате проведения полного анализа с учетом частотной зависимости [7] можно получить условие для области прозрачности
где Теперь кратко перечислим основные результаты, относящиеся к нелинейной восприимчивости Заметим, что в (15.2) можно переставлять местами два последних индекса, поэтому иногда удобно применять обозначения
и тогда (15.2) можно представить как произведение матриц
Например, для кристалла Для оценки восприимчивостей в простых диэлектриках воспользуемся следующим рассуждением: когда внешнее поле сравнивается с внутриатомным
§16. МОДЕЛЬ АНГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА
Для расчета линейной части поляризации вещества полезной оказалась модель гармонического осциллятора, применяемая в настоящее время при расчете ионной поляризуемости кристаллов. Качественно ее можно применять для оценки электронной поляризуемости. В этом случае электроны вещества выступают как гармонические осцилляторы, обладающие собственными частотами, которые соответствуют наблюдаемым спектральным линиям. Переменное электрическое поле, действуя на оптический электрон, вызывает вынужденные колебания гармонического осциллятора. Положим, что
где
Таким образом, с каждым электроном связан дипольный момент
где введена функция
для которой справедливо условие
Обычно величину
называют коэффициентом поляризуемости. Коэффициент линейной восприимчивости
где
где
Выражения (16.6), (16.7) описывают зависимость от частоты линейной восприимчивости Хотя квантовая механика построена на совершенно новых принципах, однако применение ее к данной задаче не меняет качественного описания на основе механики Ньютона. Изменения в основном коснулись количественных характеристик, а именно: выражение (16.7) сохраняет свой вид за исключением того, что собственную частоту необходимо заменить частотой перехода:
где
Называемым силой осциллятора, которая для этого электрона определяется вероятностью спонтанного перехода
то есть в конечном счете определяется интенсивностью спонтанного излучения с соответствующего уровня энергии. Если в квантовой системе полное число электронов равно
Например, для атома водорода при переходе По мере увеличения амплитуды электрического поля возрастает амплитуда колебаний осциллятора. Особенно сильно это проявляется в условиях, близких к резонансу, в которых уже необходимо учесть ангармонизм колебаний. Поэтому для описания нелинейной части поляризации вещества полезной оказалась модель ангармонического осциллятора. В связи с этим вместо уравнения (16.1) будем иметь
где ангармоничность колебаний учитывается слагаемыми Если гармонический осциллятор подвергается воздействию нескольких переменных электрических полей, то каждое из полей действует независимо от другого и конечная координата осциллятора есть простая сумма отклонений для каждого поля в отдельности. Однако эта независимость уже не имеет места для ангармонического осциллятора, сколько малыми ни были бы величины Пусть электрон находится в поле двух электрических волн с частотами
где
Решение уравнения (16.15) имеет вид, аналогичный (16.2),
Или в более компактной форме
где Подставляя (16.19) в уравнение (16.16), получим его решение в следующем виде
где
Заметим, что Прохождение через вещество одной волны приводит к эффекту генерации второй гармоники – волны на частоте
Аналогичным путем выводится нелинейная восприимчивость
где частоты Из (16.23) видно, что нелинейная восприимчивость третьего порядка резко меняется в следующих резонансных случаях: Рассмотренные особенности изменения нелинейных восприимчивостей
Аналогичную связь можно найти и для
§17. ОБЩАЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТЕЙ ДЛЯ ПРОИЗВОЛЬНОЙ КВАНТОВОМЕХАНИЧЕСКОЙ СИСТЕМЫ
Эволюция произвольной квантовомеханической системы во времени описывается уравнением для матрицы плотности
где гамильтониан
Это так называемые операторы Лиувилля, действующие согласно этим правилам в пространстве обычных операторов (а не волновых функций), в связи с чем и называются супероператорами. Уравнение для матрицы плотности в этих обозначениях запишется в виде
Переход к представлению взаимодействия можно совершить, вводя новую матрицу плотности
для которой уравнение (17.4) преобразуется в
Общее решение уравнения (17.6) представляют в виде ряда (в чем легко убедиться непосредственной проверкой):
Возвращаясь к исходному виду, получим для матрицы плотности общее решение в окончательном виде
Это решение совместно с общим выражением для средней плотности тока
В дипольном приближении Если квантовая система замкнута, то супероператор В подсистему могут быть включены парамагнитные ионы, которые можно иногда считать изолированными друг от друга, но тем не менее с каждым ионом путем сверхтонкого взаимодействия связано некоторое количество соседних ядер (ион хрома в решетке корунда взаимодействует с ядрами алюминия). В большую часть – резервуар – включен весь остальной кристалл (или его часть – фононы, магноны и т.д.). Для подсистемы степени свободы во времени меняются в соответствии со взаимодействием отдельных ее частей (ион плюс ядра). Для резервуара степени свободы практически не зависят от наличия подсистемы, так что будем полагать, что резервуар находится в состоянии теплового равновесия. При таком подходе к вычислению “отклика” среды на внешнее воздействие необходимо знать лишь матрицу плотности подсистемы. Поэтому предварительно проводят усреднение интересующих величин в зависимости от состояния резервуара и тем самым исключают из рассмотрения степени свободы резервуара. Этот подход применяется в теории релаксации [10], и именно с этой целью удобно использовать методику супероператоров. В общем случае взаимодействие подсистемы и резервуара приводит к перенормировке уровней энергии подсистемы и смешиванию ее состояний. Супероператор для подсистемы не сводится к виду (17.2). Лишь в простых случаях (невырожденные системы, малые взаимодействия) происходит сдвиг уровней подсистемы и появляется экспоненциальное затухание возбужденных состояний. Иными словами, для подсистемы, взаимодействующей с термостатом, справедливо описание с помощью неэрмитового гамильтониана. В общем случае, особенно когда имеет место вырождение уровней, супероператор Для невырожденных систем с затуханием действие супероператора
где В этом случае для монохроматических полей матрица плотности (17.9) принципиально вычисляется до конца. Вычисления носят простой характер, однако сложность и громоздкость окончательных выражений увеличивается с ростом порядка приближения по степени поля. Приведем конечные формулы. В дипольном приближении вместо тока
где
где структура первых трех слагаемых представлена формулами (14.4), (14.6) и (14.7) с учетом тензорного характера восприимчивостей типа (14.8). Восприимчивости первых двух порядков имеют вид:
Здесь Как видно из последней формулы и из классического результата (16.21), частотная зависимость квантово-механической системы количественно отличается от восприимчивости классической системы, хотя качественно они соответствуют друг другу. Для восприимчивости третьего порядка приведем лишь выражение, ответственное за генерацию третьей гармоники:
Интересно сравнить классическое выражение (16.23) и последнее (17.16). Оба содержат резонансы при
Глава IV
Уравнение движения. Эволюция механической системы однозначно определяется её состоянием в начальный момент времени и динамическими уравнениями Ньютона:(d/dt) p = f, где p =m v есть импульс материальной точки, m-её масса, а f -сила, действующая на неё. Критерий измеримости. Не существует принципиальных ограничений на точность и одновременность измерения физических величин, определяющих динамику механических систем.
Постулат тождественности Существует два различных типа элементарных частиц: фермионы и бозоны. Фермионы (электроны, протоны, нейтроны и др.) описываются антисимметричными волновыми функциями относительно перестановки их координат. Бозоны (фотоны, пионы и др.) описываются симметричными волновыми функциями. (На примере двух частиц это можно записать так: y(х1,x2)=±y (x2,x1), где знак минус берётся для фермионов, а знак плюс для бозонов). Фермионы обладают полуцелым спином, бозоны имеют целый спин.
Глава I Классическое и квантовое описание оптического поля
§ 1. КОМЕНТАРИИ К ПОСТУЛАТАМ КВАНТОВОЙ МЕХАНИКИ И КВАНТОВОЙ ОПТИКИ
В экспериментах по интерференции и дифракции световых лучей ярко проявляются волновые свойства электромагнитного и, в частности, оптического поля излучения, тогда как при поглощении и испускании излучения атомными частицами (изолированными или входящими в состав молекул, кластеров и конденсированных фаз вещества) свет ведет себя как совокупность элементарных частиц - фотонов. Более или менее удовлетворительное описание оптических полей даёт квантовая теория (квантовая электродинамика), которая объясняет оба эти противоречивые свойства. В классической физике все физические объекты удаётся четко подразделить на волны и частицы (или на объекты, состоящие из совокупности таких образований). Однако для реальных физических явлений понятия волны и частицы являются приближенными, и нельзя провести строгой границы между ними. То, что представляет собой волну в классическом понимании, при определенных условиях может вести себя как частица или их совокупность (например, фононы для звука, фотоны для света и т.д.). И наоборот, то, что по классическим представлениям считается частицами, может образовывать чисто классические волны (например, электроны в куперовских парах в сверхпроводниках). Из многочисленных экспериментов, сделанных главным образом в начале ХХ века, стало ясно, что и фотоны и атомные частицы проявляет себя одновременно в двух аспектах: волновом и корпускулярном. Причём нельзя, например, рассматривать свет ни как поток классических корпускул, ни как суперпозицию классических волн, не входя в противоречие с экспериментом. То же касалось и атомных частиц. Если придерживаться классической физики, то связное и непротиворечивое описание всей совокупности того или иного физического явления атомного масштаба невозможно. В зависимости от условий эксперимента для его истолкования приходится неизбежно прибегать к одному из двух несовместимых представлений: или потоку корпускул, или суперпозиции волн. При этом возникающий дуализм волна - частица следует интерпретировать на статистической основе, постулируя, что интенсивность соответствующей волны в некоторой точке пространства пропорциональна вероятности обнаружения в этой точке соответствующей корпускулы. Из эксперимента также однозначно следовало квантование значений некоторых физических величин, например таких, как энергетические уровни атомов или квантование ориентации магнитных моментов электронов, ядер, атомов и молекул. Эти факты делали несостоятельной концепцию, согласно которой вещество состоит из корпускул, движение которых подчинено законам классической механики. Современная квантовая механика позволяет преодолеть эти трудности, по крайней мере в нерелятивистском приближении для материальных частиц. Обратимся к краткому рассмотрению основных положений современной квантовой теории в сравнении с классической (см. приложение А). Уже беглый просмотр их показывает, что они совсем не так ясны и понятны как постулаты классических теорий. Они потеряли наглядность. Для их понимания требуется освоить новый математический язык. Это не должно нас удивлять, ибо мы пытаемся проникнуть в области атомных масштабов, где большинство наших привычных представлений, выработанных на чувственном, повседневном опыте, вовсе не обязаны быть адекватными. Представьте на минуту, что мы были бы двумерными существами типа амёб и жили бы на поверхности шара. Мы не смогли бы наглядно представить шар, так как наш чувственный опыт был бы основан на круге. Шар нам казался бы "странным кругом". В первом постулате, в отличие от кла
|
|||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 540; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.108.110 (0.019 с.) |

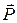 зависит от конкретных параметров среды, на которую воздействует внешнее поле
зависит от конкретных параметров среды, на которую воздействует внешнее поле 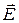 . Даже в статическом поле
. Даже в статическом поле 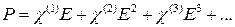 (14.1)
(14.1)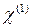 - линейная восприимчивость. Для относительно слабых электрических полей достаточно учитывать лишь этот первый член, и в таком случае можно определить диэлектрическую постоянную
- линейная восприимчивость. Для относительно слабых электрических полей достаточно учитывать лишь этот первый член, и в таком случае можно определить диэлектрическую постоянную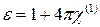 . (14.2)
. (14.2) и
и  описывают нелинейные свойства вещества. Они представляют собой вклад в нелинейную поляризацию, а коэффициенты
описывают нелинейные свойства вещества. Они представляют собой вклад в нелинейную поляризацию, а коэффициенты  и
и 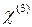 называются нелинейными восприимчивостями. Разложение в ряд по степеням поля (14.1) возможно в том случае, если существует малый параметр, например, если величина внешнего поля значительно меньше величин характерных электрических полей в веществе: внутриатомных полей, величины пробойного поля в полупроводнике и диэлектрике и др.
называются нелинейными восприимчивостями. Разложение в ряд по степеням поля (14.1) возможно в том случае, если существует малый параметр, например, если величина внешнего поля значительно меньше величин характерных электрических полей в веществе: внутриатомных полей, величины пробойного поля в полупроводнике и диэлектрике и др.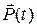 есть функционал от поля
есть функционал от поля 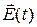 . Однако для слабых полей в указанном выше смысле такой функционал тоже можно представить в виде ряда (14.1). Необходимо лишь правильно учесть периодический характер электромагнитных волн. Это особенно просто сделать для линейной поляризации. Действительно, стационарная монохроматическая волна частоты
. Однако для слабых полей в указанном выше смысле такой функционал тоже можно представить в виде ряда (14.1). Необходимо лишь правильно учесть периодический характер электромагнитных волн. Это особенно просто сделать для линейной поляризации. Действительно, стационарная монохроматическая волна частоты  и амплитуды
и амплитуды 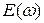 индуцируют в веществе волну поляризации той же частоты и амплитуды
индуцируют в веществе волну поляризации той же частоты и амплитуды 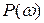 , так что в линейном приближении имеем
, так что в линейном приближении имеем , (14.3)
, (14.3)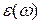 .
.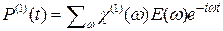 , (14.4)
, (14.4) , задаваемого выражением
, задаваемого выражением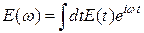 ,
,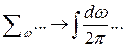
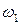 и
и  и амплитудами
и амплитудами 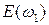 и
и  должна иметь вид
должна иметь вид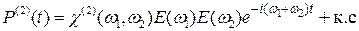 . (14.5)
. (14.5) , естественно, такая же волна может возникнуть и на частоте
, естественно, такая же волна может возникнуть и на частоте  . Если в веществе распространяются несколько волн, то необходимо составить между ними всевозможные парные комбинации типа (14.5) и затем сложить, так что окончательно получим
. Если в веществе распространяются несколько волн, то необходимо составить между ними всевозможные парные комбинации типа (14.5) и затем сложить, так что окончательно получим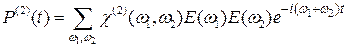 , (14.6)
, (14.6)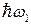 и
и 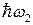 и “рождение” кванта
и “рождение” кванта  .
.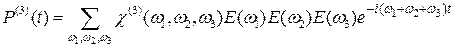 (14.7)
(14.7)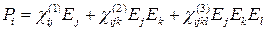 . (14.8)
. (14.8)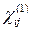 ;
; 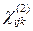 ;
; 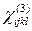 ; … определяется исключительно точечной группой симметрии кристалла, причем в этом смысле они полностью соответствуют пьезоэлектрическим тензорам[2], например в кристаллах с центром инверсии
; … определяется исключительно точечной группой симметрии кристалла, причем в этом смысле они полностью соответствуют пьезоэлектрическим тензорам[2], например в кристаллах с центром инверсии  .
.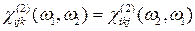 ; (15.1)
; (15.1)
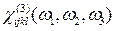 .
.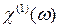 согласно (14.2) описывает показатель преломления
согласно (14.2) описывает показатель преломления 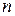 и коэффициент поглощения
и коэффициент поглощения 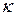 :
: 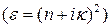 . Далее,
. Далее, 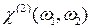 описывает сложение частот
описывает сложение частот  - явление электрооптического эффекта. Нетрудно видеть, что
- явление электрооптического эффекта. Нетрудно видеть, что 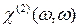 обозначает процесс генерации второй гармоники, а
обозначает процесс генерации второй гармоники, а 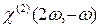 - изменение амплитуды основной волны за счет генерации второй гармоники. Коэффициент
- изменение амплитуды основной волны за счет генерации второй гармоники. Коэффициент  описывает эффект выпрямления.
описывает эффект выпрямления.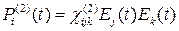 . (15.2)
. (15.2) ;
;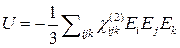 , (15.3)
, (15.3)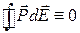
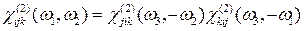 , (15.4)
, (15.4)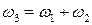 . Из условия (15.4) видно, что
. Из условия (15.4) видно, что  , а
, а 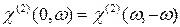 , то есть коэффициенты, ответственные за электрооптический эффект и эффект выпрямления, равны.
, то есть коэффициенты, ответственные за электрооптический эффект и эффект выпрямления, равны.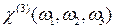 , причем
, причем 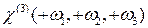 описывает генерацию гармоники
описывает генерацию гармоники 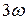 , а
, а  - самофокусировку, самоканализацию волн и двухфотонное поглощение. Далее,
- самофокусировку, самоканализацию волн и двухфотонное поглощение. Далее, 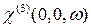 - квадратичный эффект Керра,
- квадратичный эффект Керра, 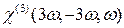 - комбинационное рассеяние волны частоты
- комбинационное рассеяние волны частоты 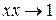 ;
;  ;
; ;
; 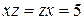 ; (15.5)
; (15.5)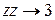 ;
; 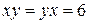 ;
;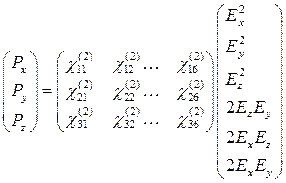 . (15.6)
. (15.6) (КДР), который относится к тетрагональной системе и имеет точечную группу симметрии
(КДР), который относится к тетрагональной системе и имеет точечную группу симметрии 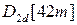 , ненулевыми компонентами являются
, ненулевыми компонентами являются 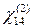 ,
, 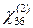 и
и 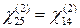 , то есть всего две. Однако согласно правилу Клейнмана
, то есть всего две. Однако согласно правилу Клейнмана 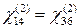 . Таким образом, лишь один из элементов тензора нелинейной восприимчивости, именно
. Таким образом, лишь один из элементов тензора нелинейной восприимчивости, именно 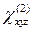 , определяет все нелинейно-оптические свойства КДР в области прозрачности.
, определяет все нелинейно-оптические свойства КДР в области прозрачности.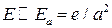 , то смещение зарядов будет порядка постоянной решетки (или боровского радиуса
, то смещение зарядов будет порядка постоянной решетки (или боровского радиуса 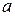 ), поэтому средний дипольный момент единицы объема
), поэтому средний дипольный момент единицы объема 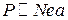 . Таким образом, из (14.1) видно, что
. Таким образом, из (14.1) видно, что 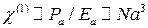 ; далее,
; далее, 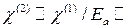 ,
, 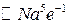 ,
, 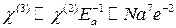 .
.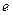 – заряд электрона,
– заряд электрона, 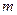 - его масса, а
- его масса, а 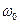 – собственная частота. Под действием электрического поля частоты
– собственная частота. Под действием электрического поля частоты 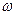 и амплитуды
и амплитуды 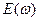 электрон отклоняется в сторону действия поля, а изменение его координаты
электрон отклоняется в сторону действия поля, а изменение его координаты  во времени описывается уравнением Ньютона
во времени описывается уравнением Ньютона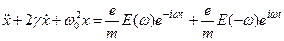 , (16.1)
, (16.1)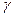 - постоянная затухания. Частное решение уравнения (16.1), описывающего вынужденные колебании, имеет следующий вид
- постоянная затухания. Частное решение уравнения (16.1), описывающего вынужденные колебании, имеет следующий вид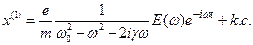 (16.2)
(16.2) ., (16.3)
., (16.3)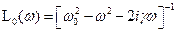 , (16.4)
, (16.4)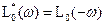
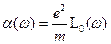 . (16.5)
. (16.5) связан с коэффициентом поляризуемости, и эта связь особенно проста для газа
связан с коэффициентом поляризуемости, и эта связь особенно проста для газа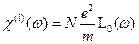 , (16.6)
, (16.6)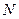 - число электронов в единице объема. Для плотной среды она сложнее, но принципиально ничего не меняется. Если в атоме, молекуле или элементарной ячейке кристалла имеется несколько электронов, обладающих различными частотами
- число электронов в единице объема. Для плотной среды она сложнее, но принципиально ничего не меняется. Если в атоме, молекуле или элементарной ячейке кристалла имеется несколько электронов, обладающих различными частотами 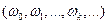 и число электронов с частотой
и число электронов с частотой 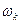 есть
есть 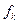 , то вместо (16.5) следует использовать общую формулу
, то вместо (16.5) следует использовать общую формулу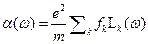 , (16.7)
, (16.7)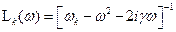 (16.8)
(16.8)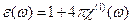 , коэффициента поглощения “
, коэффициента поглощения “ 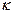 ” и показателя преломления вещества “
” и показателя преломления вещества “  ”, которые определяются формулой
”, которые определяются формулой  . Именно таким путем удается объяснить эффект аномальной дисперсии – зависимость показателя преломления от частоты, причем все рассматривается в рамках классической механики.
. Именно таким путем удается объяснить эффект аномальной дисперсии – зависимость показателя преломления от частоты, причем все рассматривается в рамках классической механики.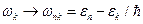 , (16.9)
, (16.9) и
и 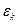 - энергетические уровни атома, молекулы или какой-либо другой квантовой системы. Число электронов с частотой
- энергетические уровни атома, молекулы или какой-либо другой квантовой системы. Число электронов с частотой  , (16.10)
, (16.10)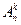 из состояния
из состояния  , (16.11)
, (16.11) , то
, то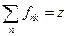 . (16.12)
. (16.12)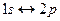 соответствующая сила осциллятора равна 0,4162. Поскольку в этом случае
соответствующая сила осциллятора равна 0,4162. Поскольку в этом случае 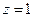 , то всем остальным переходам, в том числе и переходам из непрерывного спектра на уровень
, то всем остальным переходам, в том числе и переходам из непрерывного спектра на уровень  , соответствует сумма сил осцилляторов, равная 0,5838.
, соответствует сумма сил осцилляторов, равная 0,5838. , (16.13)
, (16.13)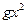 и
и 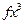 , причем каждое последующее слагаемое дает вклад, значительно меньший предыдущего:
, причем каждое последующее слагаемое дает вклад, значительно меньший предыдущего: 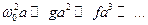 , где
, где 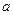 - амплитуда колебаний осциллятора.
- амплитуда колебаний осциллятора.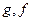 и т.д.
и т.д. и с амплитудами
и с амплитудами  . Тогда решить уравнения (16.13) можно методом последовательных приближений, полагая, что
. Тогда решить уравнения (16.13) можно методом последовательных приближений, полагая, что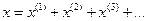 , (16.14)
, (16.14) Подставляя (16.14) в (16.13) и ограничиваясь первыми слагаемыми в наинизшем нелинейном приближении, получим следующую систему уравнений:
Подставляя (16.14) в (16.13) и ограничиваясь первыми слагаемыми в наинизшем нелинейном приближении, получим следующую систему уравнений: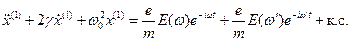 ; (16.15)
; (16.15) ; (16.16)
; (16.16)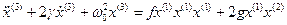 . (16.17)
. (16.17)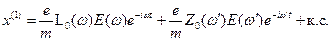 (16.18)
(16.18)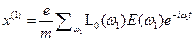 , (16.19)
, (16.19) .
. , (16.20)
, (16.20)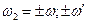 . Из (16.20) видно, что ангармонический осциллятор испытывает колебания на удвоенный частотах
. Из (16.20) видно, что ангармонический осциллятор испытывает колебания на удвоенный частотах 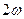 и
и 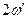 (вторые гармоники), на суммарных и разностных частотах
(вторые гармоники), на суммарных и разностных частотах  (комбинарные частоты), а также имеется постоянное во времени смещение (эффект выпрямления). С каждым таким колебанием связан соответствующий дипольный момент
(комбинарные частоты), а также имеется постоянное во времени смещение (эффект выпрямления). С каждым таким колебанием связан соответствующий дипольный момент 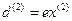 , и по аналогии с линейной восприимчивостью (16.6) можем записать нелинейную восприимчивость:
, и по аналогии с линейной восприимчивостью (16.6) можем записать нелинейную восприимчивость: . (16.21)
. (16.21) резко возрастает при резонансах
резко возрастает при резонансах 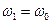 ,
, 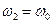 ,
, 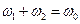 .
.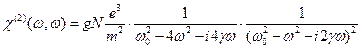 . (16.22)
. (16.22)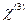 . В последнем случае надо рассматривать взаимодействие трех волн с частотами
. В последнем случае надо рассматривать взаимодействие трех волн с частотами  и амплитудами
и амплитудами 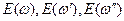 . Конечный результат имеет вид
. Конечный результат имеет вид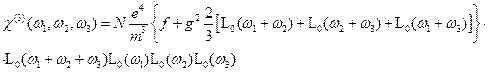 , (16.23)
, (16.23) ,
,  и
и  принимают значения
принимают значения 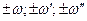 .
.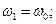

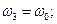
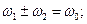
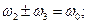
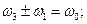
 .
.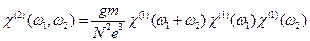 .
. , (17.1)
, (17.1)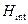 относится к взаимодействию системы с внешним полем. Формальный вывод решения уравнения (17.1) можно получить путем следующего рассмотрения. В дальнейшем удобно использовать новые операторы, которые определяются правилами
относится к взаимодействию системы с внешним полем. Формальный вывод решения уравнения (17.1) можно получить путем следующего рассмотрения. В дальнейшем удобно использовать новые операторы, которые определяются правилами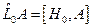 ; (17.2)
; (17.2) . (17.3)
. (17.3)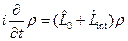 . (17.4)
. (17.4) , (17.5)
, (17.5)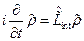 ; (17.6)
; (17.6)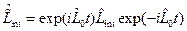 . (17.7)
. (17.7)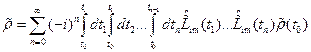 . (17.8)
. (17.8)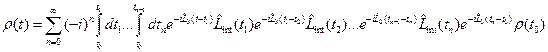 . (17.9)
. (17.9)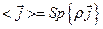 , (17.10)
, (17.10)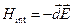 , где
, где  - дипольный момент квантовой системы. Поэтому из (17.10) с учетом (17.9) и формулы (17.3) видно, что наведенный ток представляется в виде ряда по степеням электрического поля.
- дипольный момент квантовой системы. Поэтому из (17.10) с учетом (17.9) и формулы (17.3) видно, что наведенный ток представляется в виде ряда по степеням электрического поля. просто определяется через матричные элементы гамильтониана
просто определяется через матричные элементы гамильтониана 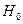 согласно (17.2). Однако в ряде случаев (газ атомов или молекул, парамагнитные ионы в кристалле, оптические центры в твердых телах) квантовая система может быть разделена на две части: малую (подсистема) и большую (резервуар).
согласно (17.2). Однако в ряде случаев (газ атомов или молекул, парамагнитные ионы в кристалле, оптические центры в твердых телах) квантовая система может быть разделена на две части: малую (подсистема) и большую (резервуар).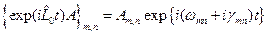 , (17.11)
, (17.11) ,
, 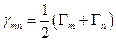 ,
,  - полуширина энергетического уровня
- полуширина энергетического уровня 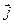 вычисляют макроскопический дипольный момент
вычисляют макроскопический дипольный момент  :
: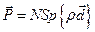 , (17.12)
, (17.12)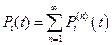 , (17.13)
, (17.13)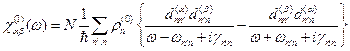 ; (17.14)
; (17.14) . (17.15)
. (17.15)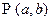 - операция перестановки величин.
- операция перестановки величин.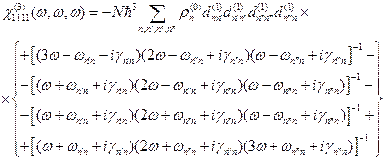 . (17.16)
. (17.16)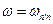 ,
, 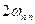 ,
,  (для классики:
(для классики: 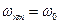 ). Однако промежуточный резонанс
). Однако промежуточный резонанс 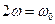 имеет место лишь для квадратичного ангармонизма, который довольно часто отсутствует. Кроме того, видно, что резонанс на основной частоте обладает особенностью третьего порядка для анграмонического осциллятора, тогда как для квантово-механической системы (атом, молекула) эта особенность первого порядка.
имеет место лишь для квадратичного ангармонизма, который довольно часто отсутствует. Кроме того, видно, что резонанс на основной частоте обладает особенностью третьего порядка для анграмонического осциллятора, тогда как для квантово-механической системы (атом, молекула) эта особенность первого порядка.


