
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 5. Квантовое статистическое распределение.Содержание книги
Поиск на нашем сайте
Решая квантовомеханическую задачу, мы по существу делим Вселенную на две части: изучаемую систему и остальную часть Вселенной. Далее мы действуем так, как если бы интересующая нас система составляла всю Вселенную. Рассмотрим, что происходит, когда мы включаем в рассмотрение остальную часть Вселенной. Рассмотрим систему, которую с нужной нам степенью точности можно считать замкнутой и которая включает интересующую нас систему. Будем рассматривать эту замкнутую систему как всю Вселенную. Тогда к этой замкнутой системе применим обычный аппарат квантовой механики. Точный гамильтониан всей Вселенной имеет вид
Здесь Давайте вначале пренебрежем взаимодействием рассматриваемой системы с остальной частью Вселенной т.е. положим Как хорошо известно, переменные в уравнении Шредингера с таким гамильтонианом
Вторая функция -
Таким образом, в этом случае мы можем выделенной нами системе и окружающей ее среде приписать собственные волновые функции: нашей системе – функцию Итак, в том случае, когда мы пренебрегаем взаимодействием интересующей нас системы со своим окружением, мы можем нашей системе приписать ее собственную волновую функцию, которая зависит от ее координат и не зависит от координат окружающей среды. Используя эту волновую функцию, мы можем с помощью известного вам аппарата квантовой механики описать интересующую нас систему наиболее подробным в квантовой механике образом. Т.е. зная волновую функцию нашей системы в интересующем нас состоянии движения, мы можем. в каждый момент времени совершенно четко определить для этого состояния вероятности всех физических величин, характеризующих нашу систему, и, соответственно, вычислить средние значения всех таких физических величин. В частности мы можем, опираясь на множество волновых функций нашей системы, определить линейные пространства векторов состояний нашей системы. Ситуация существенно изменится, если мы учтем взаимодействие выделенной нами системы с остальной частью Вселенной. В этом случае гамильтониан всей Вселенной уже нельзя представить в виде суммы двух операторов, один из которых действует только на координаты нашей системы, а второй – только на координаты ее окружения. В результате переменные в уравнении Шредингера не разделяются, и волновую функцию Пусть замкнутая находится в состоянии с волновой функцией
Договоримся о следующей терминологии. Когда мы учитываем взаимодействие выделенной нами части Вселенной со своим окружением, условимся волновой функцией этой части Вселенной называть именно волновую функцию, которая осуществляет описание этой части в случае, когда мы пренебрегаем ее взаимодействием с остальной Вселенной. Соответственно, под векторами состояний выделенной части мы будем понимать векторы состояний линейного пространства, построенного на основе волновых функций выделенной части. Выделим во Вселенной некоторую ее часть и будем интересоваться ее описанием. Пусть
Соответствующий бра-вектор имеет вид
Пусть имеется линейный оператор
Найдем среднее значение оператора в состоянии всей Вселенной, описываемом векторами состояний
Подставляем разложение (5) и (6) векторов состояния всей Вселенной. При этом учитываем, что оператор
В силу ортонормированности базиса скалярное произведение
С учетом этого выражение для среднего принимает вид
Выделим сумму по числам, задающим векторы базисного набора окружения нашей системы
Введем в рассмотрение матрицу
Тогда выражение для среднего примет вид
Матрица Например, в качестве базиса линейного пространства нашей системы мы можем взять векторы, отвечающие стационарным состояниям нашей системы, которые она имела бы, если бы не взаимодействовала с окружающей средой. Тогда индекс Будем теперь каждому Кэт-вектору линейного пространства нашей системы ставить в соответствие определенный Кэт-вектор этого же пространства по следующему закону. Кэт-вектору
где - Указав такой закон, мы с вами однозначным образом определили линейный оператор
Особо подчеркну, что определенный нами оператор Через оператор
Выделим сумму по
В выражении
Здесь у нас в роли вектора
Воспользовавшись свойством линейности оператора
Выражение
Таким образом, получаем
Подставляя (23) в выражение (18) для среднего значения
Выражение стоящее справа есть шпур произведения двух операторов, который обозначается как
Если То, что у нас в результате получился шпур не случайно. Дело в том, что среднее значение физической величины не должно зависеть от того, какой базис для ее расчета мы используем. Шпур же как раз и инвариантен относительно выбора базиса. Это означает следующее. Пусть у нас имеются два различных ортонормированных базиса
Итак, если нам известен оператор Перейдем теперь к вопросу о вычислении статистических средних операторов в состоянии термодинамического равновесия нашей системы. Будем считать число частиц в нашей системе фиксированным, и будем рассматривать операторы, которые в шредингеровском представлении не зависят явно от времени. Тогда матричные элементы оператора
Тогда если мы фиксируем оригинал
Теперь для того, чтобы получить статистическое среднее интересующей ее величины нужно квантовмеханическое ожидание (25) ее оператора усреднить по времени
Воспользовавшись тем, что среднее суммы есть сумма средних, а также тем, что матричные элементы
Введем теперь в рассмотрение матрицу
Тогда статичтическое среднее запишется как
Аналогично тому, как мы ранее вводили оператор
Тогда выражение для статистического среднего примет вид
Действуя так же как и выше, мы можем записать (34) в виде
где шпур может быть вычислен по любому фиксированному (т.е. не зависящему от времени) ортонормированному базису линейного пространства нашей системы. Как легко видеть непосредственно из определения (31), Таким образом, матричные элементы статистической матрицы плотности удовлетворяют условию
Таким образом, матица В общем виде запись оператора
Поскльку
Следовательно, через собственный ортонормированный базис
Для того, чтобы установить следующее свойство собственных значений оператора
По определению тождественного оператора
Таким образом, в силу нормировки
Следовательно, статистическое среднее этого оператора
С другой стороны, мы можем вычислить статистическое среднее нашего оператора как
Будем вычислять шпур по собственному базису
Сравнивая выражения (42) и (44) для статистического среднего тождественного оператора, приходи к выводу, что в состоянии термодинамического равновесия сумма всех собственных значений статистического оператора
Для того, чтобы установить еще одно свойство собственных значений оператора
проекции на собственный вектор
При разложении вектора Дирака
Действуем на
Далее учитываем, что наш оператор (46) относится только к нашей системе. Поэтому в данной сдвоенной записи он не затрагивает векторов
Учитывая конкретный вид (46) оператора
В силу ортонормированности базиса
Таким образом,
Подставляем (53) в (49).
Умножаем Кэт-вектор
Используя свойство скалярного произведения
Получаем
Согласно правилу скалярного умножения сдвоенных записей скалярно перемножать можно только бра- и Кэт векторы линейного пространства одной и той же подсистемы. Следовательно, в нашем случае
В силу ортонормированности базисов скалярные произведения
и
Учтя это, получаем
Следовательно, с одной стороны статистическое среднее нашего оператора (46) есть
С другой стороны, его статистическое среднее можно вычислить как
Будем вычислять шпур по собственному базису
Учитывая конкретный вид нашего оператора
Таким образом, искомое статистическое среднее есть
Вспомнив, что диагональные матричные элементы оператора в его собственном базисе равны его соответствующим собственным значениям, получаем что статистическое среднее оператора проекции на собственный вектор
Сравнивая выражения (61) и (65), получаем
Отсюда видно, что все собственные значения оператора
Итак, состояние равновесия нашей системы мы можем описать эрмитовым оператором
который обладает следующими свойствами: 1) его собственные векторы 2) его собственные значения 3) Статистическое среднее любого на зависящего от времени эрмитового оператора
Теперь основная наша задача состоит в том, чтобы найти собственный базис оператора Для этого в квантовой статистической теории делают приближение в некотором смысле аналогичное тому, которое делается в классической статистике. Как известно, из эксперимента, независимо от природы макроскопической системы ее равновесное состояние задается внешними параметрами и температурой. Внешние параметры характеризуют влияние на нашу систему окружающей среды, которое с достаточной точностью может быть аппроксимировано чисто силовым стационарным воздействием окружающей среды на нашу систему. Также как и в классической теории, совокупность координат изучаемой нами системы мы будем обозначать В классической теории, пользуясь тем, что в состоянии равновесия отсутсвуют макроскопические потоки и система с подавляющей вероятностью находится в состояниях с энергией, близкой к своему среднему значению, мы мы очень-очень сложную точную функцию Гамильтона замкнутой системы, состоящей из нашей системы и окружающей среды, заменяли на приближенную функцию Гамильтона
Влияние окружающей среды на нашу систему, которое с достаточной точностью может быть аппроксимировано чисто силовым стационарным воздействием на нашу систему, мы учитываем путем введения в эффективную функцию Гамильтона Понятно, что аналогичным образом мы должны поступать и в квантовой статистической теории. При рассмотрении системы, находящейся в тепловом равновесии с окружающей средой мы очень-очень сложный оператор Гамильтона всей замкнутой системы, состоящей из нашей системы и окружающей среды, заменяем на приближенный оператор Гамильтона
Влияние окружающей среды на нашу систему, которое может быть с достаточной точностью аппроксимировано чисто силовымстационарным воздействием на нашу систем, мы учитываем путем введения в эффективный оператор Гамильтона, приписываемый нашей системе, параметрической зависимости от внешних параметров. При этом внешние параметры Например, идеальному газу в сосуде с жесткими стенками мы приписываем функцию Гамильтона
где
- внешний для нашего газа потенциал, который моделирует влияние на наш газ стенок. Собственные функции и собственные значения оператора Гамильтона, приписываемого нашей системе, т.е. решения стационарного уравнения Шредингера
понятно, будут зависеть от внешних параметров. Далее вспомним, как в квантовой механике определяется производная по времени от физической величины. В квантовой механике, как вы знаете, производную
При описании равновесного состояния макроскопической системы в статистическом подходе мы должны еще усреднять по временному интервалу
Как мы уже обсуждали, основным свойством равновесного состояния макроскопической системы я
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 387; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.200.247 (0.015 с.) |

 . (1)
. (1)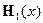 - гамильтониан нашей системы, который в случае, если бы наша система была изолирована, входил бы в уравнение Шредингера для нашей системы,
- гамильтониан нашей системы, который в случае, если бы наша система была изолирована, входил бы в уравнение Шредингера для нашей системы,  - гамильтониан остальной части Вселенной,
- гамильтониан остальной части Вселенной, 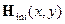 - член, описывающий взаимодействие нашей системы с остальной частью Вселенной. Причем этот член гамильтониана описывает не действие, а именно взаимодействие, т.е. не может быть представлен в виде суммы двух операторов, один из которых действует только на координаты рассматриваемой системы, а другой – только на координаты остальной части Вселенной. Вообще, если говорить строго, то в природе не бывает действия, бывает только взаимодействие. Т.е. две системы влияют друг на друга самосогласованным образом. Когда мы с вами говорим о внешнем силовом поле, приложенном к рассматриваемой системе, мы делаем, на самом деле, приближение. Мы идеализируем окружающую среду, представляя ее в виде классических источников силового поля, на состояние которых наша система не оказывает никакого влияния. С математической точки зрения, член
- член, описывающий взаимодействие нашей системы с остальной частью Вселенной. Причем этот член гамильтониана описывает не действие, а именно взаимодействие, т.е. не может быть представлен в виде суммы двух операторов, один из которых действует только на координаты рассматриваемой системы, а другой – только на координаты остальной части Вселенной. Вообще, если говорить строго, то в природе не бывает действия, бывает только взаимодействие. Т.е. две системы влияют друг на друга самосогласованным образом. Когда мы с вами говорим о внешнем силовом поле, приложенном к рассматриваемой системе, мы делаем, на самом деле, приближение. Мы идеализируем окружающую среду, представляя ее в виде классических источников силового поля, на состояние которых наша система не оказывает никакого влияния. С математической точки зрения, член 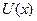 этого классического эффективного поля. В качестве примера можно привести задачу о спектре свободного атома. В этой задачи имеется два упрощающих обстоятельства. Первое обстоятельство заключается в том, что масса ядра существенно превышает массу электронной подсистемы, и второе обстоятельство – это то, что размер ядра существенно меньше размера атома. Эти два обстоятельства позволяют идеализировать задачу и при расчете спектра атома рассматривать систему из
этого классического эффективного поля. В качестве примера можно привести задачу о спектре свободного атома. В этой задачи имеется два упрощающих обстоятельства. Первое обстоятельство заключается в том, что масса ядра существенно превышает массу электронной подсистемы, и второе обстоятельство – это то, что размер ядра существенно меньше размера атома. Эти два обстоятельства позволяют идеализировать задачу и при расчете спектра атома рассматривать систему из  электронов, находящихся во внешнем центрально симметричном кулоновском поле неподвижного точечного классического заряда
электронов, находящихся во внешнем центрально симметричном кулоновском поле неподвижного точечного классического заряда 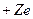 .
.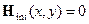 . В этом случае оператор Гамильтона всей системы
. В этом случае оператор Гамильтона всей системы  представляет собой сумму двух операторов. Один из этих операторов действует только на координаты
представляет собой сумму двух операторов. Один из этих операторов действует только на координаты 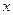 нашей системы и не затрагивает координат
нашей системы и не затрагивает координат  остальной части Вселенной. Другой напротив не затрагивает координат
остальной части Вселенной. Другой напротив не затрагивает координат  разделяются, и волновая функция
разделяются, и волновая функция 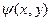 , описывающая состояние всей системы в любой момент времени представляет собой произведение двух функций (
, описывающая состояние всей системы в любой момент времени представляет собой произведение двух функций ( ). Первая из этих функций -
). Первая из этих функций -  -зависит только от координат
-зависит только от координат 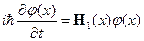 . (2)
. (2) - не зависит от координат
- не зависит от координат  . (3)
. (3) дает плотность вероятности различных конфигураций системы в данный момент времени. Соответственно,
дает плотность вероятности различных конфигураций системы в данный момент времени. Соответственно,  дает плотность вероятности различных конфигураций окружения нашей системы в данный момент времени. В частности, вероятность
дает плотность вероятности различных конфигураций окружения нашей системы в данный момент времени. В частности, вероятность 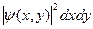 всей Вселенной находится в ее элементе конфигурационного пространства
всей Вселенной находится в ее элементе конфигурационного пространства  есть произведение вероятности
есть произведение вероятности 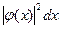 нашей системы находится в соответствующем элементе
нашей системы находится в соответствующем элементе 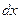 ее конфигурационного пространства на вероятность
ее конфигурационного пространства на вероятность 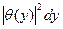 окружения нашей системы находится в соответствующем элементе
окружения нашей системы находится в соответствующем элементе  его конфигурационного пространства. В этом как раз проявлется независимость друг от друга нашей системы и окружающей среды. Нахождение нашей системы в некоторых своих конфигурациях и нахождение окружающей среды в ее конфигурациях являются статистически независимыми событиями.
его конфигурационного пространства. В этом как раз проявлется независимость друг от друга нашей системы и окружающей среды. Нахождение нашей системы в некоторых своих конфигурациях и нахождение окружающей среды в ее конфигурациях являются статистически независимыми событиями. , описывающую состояние всей Вселенной, в произвольный момент времени уже нельзя представить в виде произведения функции, зависящей только от координат нашей системы, и функции, зависящей только от координат ее окружения (
, описывающую состояние всей Вселенной, в произвольный момент времени уже нельзя представить в виде произведения функции, зависящей только от координат нашей системы, и функции, зависящей только от координат ее окружения ( ). Таким образом, для системы, взаимодействующей со своим окружением, мы не можем ввести волновую функцию, которая завесила бы только от координат системы, но не завесила от координат окружающей среды. Т.е. состоянию нашей системы уже нельзя приписать собственную. волновую функцию.
). Таким образом, для системы, взаимодействующей со своим окружением, мы не можем ввести волновую функцию, которая завесила бы только от координат системы, но не завесила от координат окружающей среды. Т.е. состоянию нашей системы уже нельзя приписать собственную. волновую функцию.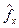 - оператор физической величины, относящейся только к интересующей нас части всей замкнутой системы. Индекс
- оператор физической величины, относящейся только к интересующей нас части всей замкнутой системы. Индекс 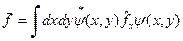 . (4)
. (4) - полный ортонормированный набор векторов состояний в векторном пространстве, описывающем нашу систему, а
- полный ортонормированный набор векторов состояний в векторном пространстве, описывающем нашу систему, а 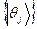 - полный ортонормированный набор векторов состояний в векторном пространстве, описывающем остальную часть Вселенной. Тогда Кэт-вектор состояния всей Вселенной можно представить через сдвоенную запись
- полный ортонормированный набор векторов состояний в векторном пространстве, описывающем остальную часть Вселенной. Тогда Кэт-вектор состояния всей Вселенной можно представить через сдвоенную запись . (5)
. (5) . (6)
. (6) , действующий только на нашу систему. Это означает, что в координатном представлении он будет действовать только на координаты нашей системы, а в нашей сдвоенной записи он будет действовать только на векторы состояний нашей системы, и не будет затрагивать векторы состояний остальной части Вселенной
, действующий только на нашу систему. Это означает, что в координатном представлении он будет действовать только на координаты нашей системы, а в нашей сдвоенной записи он будет действовать только на векторы состояний нашей системы, и не будет затрагивать векторы состояний остальной части Вселенной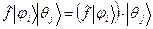 . (7)
. (7) и
и 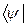 . Согласно общему правилу это среднее есть
. Согласно общему правилу это среднее есть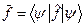 . (8)
. (8) остальной части Вселенной и пользуемся правилами работы со сдвоенной записью векторов состояний
остальной части Вселенной и пользуемся правилами работы со сдвоенной записью векторов состояний . (9)
. (9) . (10)
. (10)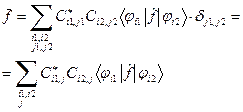 . (11)
. (11)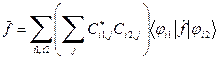 . (12)
. (12)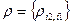 с матричными элементами
с матричными элементами . (13)
. (13) . (14)
. (14) , во-первых, содержит в себе всю информацию об окружающей среде. Во-вторых, индексы элементов матрицы
, во-первых, содержит в себе всю информацию об окружающей среде. Во-вторых, индексы элементов матрицы  есть полный набор квантовых чисел, который определяет стационарные состояния системы, которое она имела бы, если бы не взаимодействовала с окружающей средой.
есть полный набор квантовых чисел, который определяет стационарные состояния системы, которое она имела бы, если бы не взаимодействовала с окружающей средой.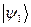 ставится в соответствие Кэт-вектор
ставится в соответствие Кэт-вектор  такой, что каждая его координаты в базисе
такой, что каждая его координаты в базисе 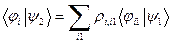 , (15)
, (15)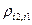 -матричные элементы введенной нами выше матрицы
-матричные элементы введенной нами выше матрицы  , действующий в линейном пространстве нашей системы, матрица которого в базисе
, действующий в линейном пространстве нашей системы, матрица которого в базисе 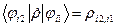 . (16)
. (16)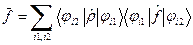 . (17)
. (17) и сумму по
и сумму по 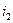 .
. . (18)
. (18) воспользуемся свойством скалярного произведения
воспользуемся свойством скалярного произведения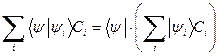 . (19)
. (19)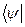 выступает вектор
выступает вектор  , в роли векторов
, в роли векторов 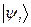 выступают векторы
выступают векторы  , а в роли чисел
, а в роли чисел 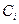 выступают числа
выступают числа  . В результате получаем
. В результате получаем . (20)
. (20)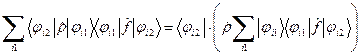 . (21)
. (21) представляет собой разложение вектора
представляет собой разложение вектора  по базису
по базису 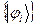
 . (22)
. (22) . (23)
. (23) . (24)
. (24) . Таким образом, получаем окончательное выражение для среднего значения оператора
. Таким образом, получаем окончательное выражение для среднего значения оператора  . (25)
. (25) и
и  , определяемые различными наборами
, определяемые различными наборами  физических величин, характеризующих нашу систему. Например, первый базис может состоять из векторов, отвечающих стационарным состояниям нашей системы, а второй – соответствовать полному набору собственных функций оператора импульса нашей системы. Шпур любого линейного оператора, в нашем случае
физических величин, характеризующих нашу систему. Например, первый базис может состоять из векторов, отвечающих стационарным состояниям нашей системы, а второй – соответствовать полному набору собственных функций оператора импульса нашей системы. Шпур любого линейного оператора, в нашем случае  , в каждом из этих базисов будет одинаков, т.е. будет справедливо равенство
, в каждом из этих базисов будет одинаков, т.е. будет справедливо равенство . (26)
. (26) по фиксированному базису
по фиксированному базису  . Действительно,
. Действительно,  в фиксированном (не зависящем от времени) ортонормированном базисе
в фиксированном (не зависящем от времени) ортонормированном базисе 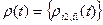 , определенной через коэффициенты разложения
, определенной через коэффициенты разложения  разложения.
разложения.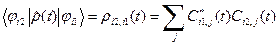 . (27)
. (27)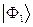 , то координаты в ортонормированном базисе
, то координаты в ортонормированном базисе 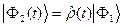 в момент времени
в момент времени  . (28)
. (28) , существенно превышающем времена микроскопических процессов
, существенно превышающем времена микроскопических процессов . (29)
. (29) оператора
оператора 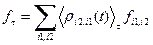 . (30)
. (30)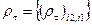 с элементами
с элементами . (31)
. (31)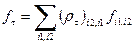 . (32)
. (32)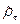 . Этот оператор мы определим как закон, который кэт-вектору
. Этот оператор мы определим как закон, который кэт-вектору  ставит в соответствие вектор
ставит в соответствие вектор такой, что каждая его координаты в базисе
такой, что каждая его координаты в базисе  . (33)
. (33)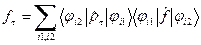 . (34)
. (34) , (35)
, (35)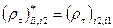 . (36)
. (36) является эрмитовой, и, соответственно, оператор
является эрмитовой, и, соответственно, оператор  образуют базис линейного пространства нашей системы.
образуют базис линейного пространства нашей системы.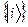
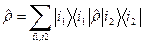 . (37)
. (37) . (38)
. (38)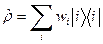 . (39)
. (39) . Квантомеханическое среднее этого оператора в состоянии
. Квантомеханическое среднее этого оператора в состоянии  всей Вселенной
всей Вселенной . (40)
. (40)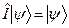 . (39)
. (39)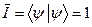 . (41)
. (41) . (42)
. (42)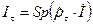 . (43)
. (43) . Тогда
. Тогда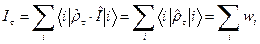 . (44)
. (44)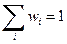 . (45)
. (45)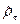 , вычислим статистическое среднее оператора
, вычислим статистическое среднее оператора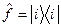 (46)
(46)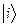 оператора
оператора  . (47)
. (47) линейного пространства нашей системы использовать собственный ортонормированный базис
линейного пространства нашей системы использовать собственный ортонормированный базис 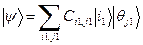 . (48)
. (48)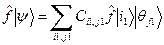 . (49)
. (49) линейного пространства окружающей среды, т.е. результат его действия на сдвоенную запись есть
линейного пространства окружающей среды, т.е. результат его действия на сдвоенную запись есть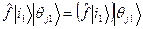 . (50)
. (50) есть
есть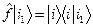 . (51)
. (51)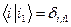 . (52)
. (52) . (53)
. (53) . (54)
. (54) на бра-вектор
на бра-вектор  . Получаем
. Получаем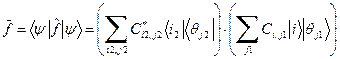 (55)
(55) , (56)
, (56) . (57)
. (57)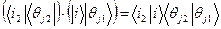 . (58)
. (58)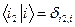 (59)
(59)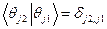 .
.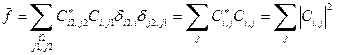 . (60)
. (60) . (61)
. (61) . (62)
. (62) . (63)
. (63) есть
есть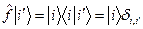 . (64)
. (64)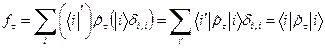 . (65)
. (65) . (65)
. (65) . (66)
. (66) . (67)
. (67)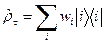 , (68)
, (68)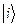 образуют ортонормированный базис линейного пространства нашей системы;
образуют ортонормированный базис линейного пространства нашей системы; являются вещественными и неотрицательными. Причем сумма всех собственных значений
являются вещественными и неотрицательными. Причем сумма всех собственных значений  .
.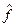 , относящегося к рассматриваемой системе, можно вычислить с помощью выражения
, относящегося к рассматриваемой системе, можно вычислить с помощью выражения . (69)
. (69) , а совокупность координат окружающей среды -
, а совокупность координат окружающей среды -  .
. , которую представляли в виде суммы эффективной функции Гамильтона нашей системы
, которую представляли в виде суммы эффективной функции Гамильтона нашей системы 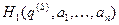 и эффективной функции Гамильтона окружающей среды
и эффективной функции Гамильтона окружающей среды 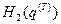
 . (70)
. (70)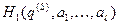 , приписываемую нашей системе, параметрической зависимости от внешних параметров. Теплообмен между нашей системой и окружающей средой мы учитывали следующим образом. Мы фиксировали функцию Гамильтона
, приписываемую нашей системе, параметрической зависимости от внешних параметров. Теплообмен между нашей системой и окружающей средой мы учитывали следующим образом. Мы фиксировали функцию Гамильтона 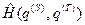 , который представляем в виде суммы эффективной функции Гамильтона нашей системы
, который представляем в виде суммы эффективной функции Гамильтона нашей системы  и эффективной функции Гамильтона окружающей среды
и эффективной функции Гамильтона окружающей среды 
 . (71)
. (71) определяют положение внешних тел и рассматриваются как числа, а не как операторы. Таким образом, состояние внешних тел мы описываем классически.
определяют положение внешних тел и рассматриваются как числа, а не как операторы. Таким образом, состояние внешних тел мы описываем классически. , (72)
, (72)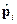 - оператор импульса i-ой частицы,
- оператор импульса i-ой частицы, (73)
(73) , (74)
, (74) по времени от физической величины
по времени от физической величины  нельзя определить как предел отношения приращения величины
нельзя определить как предел отношения приращения величины  к интервалу времени
к интервалу времени  , при стремлении
, при стремлении  . (75)
. (75) . (76)
. (76)


