
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория ландау фазовых переходов второго родаСодержание книги
Поиск на нашем сайте
Из приведенных вычислений видно, что при разного типа приближенных подсчетах потенциала Гиббса для модели Изинга на промежуточных этапах возникала некоторая функция - неравновесный потенциал, минимумы которого соответствуют потенциалам Гиббса разных фаз. Характерной чертой этой функции является "сильная нелинейность" условий ее экстремума - уравнений состояния. Именно нелинейность позволила получать разные типы решений для разных внешних условий. Наличие такой функции, единой для всех фаз, которые могут быть реализованы в модели, обеспечивает связь между численными значениями равновесных термодинамических потенциалов разных фаз при температуре перехода и их производными по температуре
Можно легко представить и другие коллективные координаты. Например, если энергия взаимодействия между моментами в модели Изинга-Ленца
Рассмотрим, какие же общие свойства переходов без скрытой теплоты (переходов второго рода) следуют только из того, что существует неравновесный потенциал Ландау. Для этого не будем конкретизировать зависимость потенциала Ландау от параметра порядка и физический смысл параметра порядка. Кроме того, рассмотрим простейший случай, когда коллективная координата, ответственная за перестройку структуры, при фазовом переходе одна, как в разобранных примерах ферромагнитных или антиферромагнитных упорядочениях моментов. Ясно, что неравновесный потенциал в этом простом случае не должен зависеть от знака параметра порядка, то есть может зависеть только от
где
Оно, как и должно быть, согласно (8), (9), имеет два типа решений
Равновесная свободная энергия, соответствующая
Еще одно интересное свойство переходов второго рода: при переходах второго рода не работает "правило фаз" Гиббса. Это правило гласит: в одной точке на фазовой р-Т диаграмме не может сосуществовать более трех фаз одного вещества. При выводе правила фаз существенно используется предположение о независимости их потенциалов Гиббса. При переходах второго рода потенциалы граничащих фаз не независимы. Поэтому сосуществование более трех фаз невозможно, а граничить в одной точке перехода второго рода могут и более трех фаз После краткого знакомства с представлениями о переходах второго рода, их свойствах и моделях, которые применяют для их описания, уместно задать вопрос: а при переходах первого рода можно ли говорить о едином неравновесном потенциале, описывающем обе фазы? Оказывается, и при переходах первого рода обычно такой единый неравновесный потенциал тоже существует. В простейшем случае модели типа Изинга потенциал Ландау, описывающий переход первого рода, представляет собой полином от
Потенциал (11) описывает переход первого рода, если
(второе решение биквадратного уравнения состояния (знак минус перед корнем) всегда соответствует максимуму В нашем кратком экскурсе осталось только сказать о том, как же можно уточнить модель Изинга-Ленца, то есть какие взаимодействия в ней нужно учесть, чтобы получить в качестве эквивалентного потенциала Ландау полином (11) с
[1] Непосредственно в интеграле (29) замену переменной делать нельзя, поскольку не существует однозначной обратной функции, определенной во всей области интегрирования от до, и, соответственно, не выполнены условия теоремы о замене переменной. А вот в каждой из областей от до 0 и от 0 до по отдельности однозначная обратная функция определена. В области до 0 она есть. В области 0 до. Поэтому в каждой из этих областей условия теоремы для такой замены переменной выполнены.
|
|||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 512; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.161.239 (0.011 с.) |

 и
и 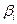 , i = 1, 2, в разложении (1). Интуитивно ясно, что такая функция, называемая неравновесным потенциалом или потенциалом Ландау, должна существовать всегда, когда структуры фаз близки между собой. Строго можно показать, что неравновесную свободную энергию (потенциал Ландау) можно ввести в рассмотрение, если в перестройке структуры при переходе из одной фазы в другую участвует ограниченное число степеней свободы кристалла - коллективных координат или параметров порядка. Коллективными эти координаты называются потому, что в их формировании участвуют степени свободы всех атомов. В приведенном примере (модели Изинга-Ленца) параметром порядка является плотность ферромагнитного момента кристалла
, i = 1, 2, в разложении (1). Интуитивно ясно, что такая функция, называемая неравновесным потенциалом или потенциалом Ландау, должна существовать всегда, когда структуры фаз близки между собой. Строго можно показать, что неравновесную свободную энергию (потенциал Ландау) можно ввести в рассмотрение, если в перестройке структуры при переходе из одной фазы в другую участвует ограниченное число степеней свободы кристалла - коллективных координат или параметров порядка. Коллективными эти координаты называются потому, что в их формировании участвуют степени свободы всех атомов. В приведенном примере (модели Изинга-Ленца) параметром порядка является плотность ферромагнитного момента кристалла .
. , то интуитивно ясно, что при низких температурах стабильной должна быть фаза, в которой моменты соседних узлов направлены в противоположные стороны (антиферромагнитный порядок). Антиферромагнитной фазе отвечает наименьшая внутренняя энергия, а энтропия при температурах, близких к нулю, играет малую роль. При чередующемся (вверх-вниз) упорядочении моментов решетку можно мыслить как разделившуюся на две подрешетки, каждая из которых намагничена ферромагнитно. Параметр порядка при антиферромагнитном упорядочении есть разность плотностей моментов подрешеток. Можно придумать и более сложные упорядочения и установить взаимодействия, приводящие к ним.
, то интуитивно ясно, что при низких температурах стабильной должна быть фаза, в которой моменты соседних узлов направлены в противоположные стороны (антиферромагнитный порядок). Антиферромагнитной фазе отвечает наименьшая внутренняя энергия, а энтропия при температурах, близких к нулю, играет малую роль. При чередующемся (вверх-вниз) упорядочении моментов решетку можно мыслить как разделившуюся на две подрешетки, каждая из которых намагничена ферромагнитно. Параметр порядка при антиферромагнитном упорядочении есть разность плотностей моментов подрешеток. Можно придумать и более сложные упорядочения и установить взаимодействия, приводящие к ним.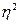 . Такие функции лучше всего аппроксимируются полиномами четных степеней относительно
. Такие функции лучше всего аппроксимируются полиномами четных степеней относительно  . Существует целая наука о том, как следует аппроксимировать произвольные функции некоторых аргументов, чтобы отразить те или иные свойства, которые обязательно характеризуют функцию, если у нее такой аргумент. Фактически именно выявлением всех обязательных особенностей занимается теория катастроф в симметричных системах. В частности, оказывается, что неравновесный потенциал Изинга-Ленца в приближении Горского-Брегга-Вильямса с точностью, качественно верно отражающей аномалии физических характеристик при переходе, эквивалентен полиному четвертой степени
. Существует целая наука о том, как следует аппроксимировать произвольные функции некоторых аргументов, чтобы отразить те или иные свойства, которые обязательно характеризуют функцию, если у нее такой аргумент. Фактически именно выявлением всех обязательных особенностей занимается теория катастроф в симметричных системах. В частности, оказывается, что неравновесный потенциал Изинга-Ленца в приближении Горского-Брегга-Вильямса с точностью, качественно верно отражающей аномалии физических характеристик при переходе, эквивалентен полиному четвертой степени , (10)
, (10) и
и  . Уравнение состояния для аппроксимирующего полинома (10) очень простое
. Уравнение состояния для аппроксимирующего полинома (10) очень простое .
. и
и  .
. . Свободная энергия, соответствующая
. Свободная энергия, соответствующая  ,
,  и формально всегда меньше
и формально всегда меньше  . Однако само решение
. Однако само решение  есть действительное число только при
есть действительное число только при 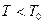 (тогда выражение под корнем положительное). В этой простой феноменологической модели легко подсчитать, что энтропия S в точке перехода изменяется непрерывно, но проявляет излом в ее температурной зависимости:
(тогда выражение под корнем положительное). В этой простой феноменологической модели легко подсчитать, что энтропия S в точке перехода изменяется непрерывно, но проявляет излом в ее температурной зависимости:  , где
, где  - энтропия неупорядоченной фазы. Соответственно в точке перехода теплоемкость С испытывает скачок
- энтропия неупорядоченной фазы. Соответственно в точке перехода теплоемкость С испытывает скачок  , причем теплоемкость возрастает при переходе в упорядоченную фазу. Согласно соотношению Эренфеста, аналогичному соотношению Клайперона-Клаузиуса для переходов первого рода, скачок теплоемкости обратно пропорционален скачку сжимаемости, причем коэффициент пропорциональности есть произведение температуры на квадрат коэффициента теплового расширения. Таким образом, при переходах второго рода испытывает скачок и коэффициент теплового расширения.
, причем теплоемкость возрастает при переходе в упорядоченную фазу. Согласно соотношению Эренфеста, аналогичному соотношению Клайперона-Клаузиуса для переходов первого рода, скачок теплоемкости обратно пропорционален скачку сжимаемости, причем коэффициент пропорциональности есть произведение температуры на квадрат коэффициента теплового расширения. Таким образом, при переходах второго рода испытывает скачок и коэффициент теплового расширения. . (11)
. (11) ,
,  . Это легко увидеть, записав решение уравнения состояния для (11) в упорядоченной фазе
. Это легко увидеть, записав решение уравнения состояния для (11) в упорядоченной фазе (12)
(12) ). Видно, что при
). Видно, что при  значение
значение 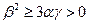 , а решение
, а решение  устойчиво при любых
устойчиво при любых 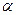 ,
,  и
и  от температуры есть область сосуществования фаз, то есть возможен температурный гистерезис: перегрев и переохлаждение фаз. Можно подсчитать скачок энтропии и скрытую теплоту при условии равенства равновесных свободных энергий фаз
от температуры есть область сосуществования фаз, то есть возможен температурный гистерезис: перегрев и переохлаждение фаз. Можно подсчитать скачок энтропии и скрытую теплоту при условии равенства равновесных свободных энергий фаз  , для чего нужно задать зависимость
, для чего нужно задать зависимость 


