
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 10. Движение электрона в кристалле в слабых полях. Метод эффективной массы. Примесные состояния в полупроводникахСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Как обсуждалось в курсе квантовой механики, в рамках приближения самосгласованного поля задача об электронной подсистеме в кристалле, сводится к задаче об идеальном электронном газе. В идеальном кристалле закон дисперсии электронов
Однако, как мы знаем, атомы примеси, как и другие структурные дефекты, могут создавать дискретные уровни в запрещенной зоне. Расчет их составляет одну из задач теории реальных кристаллов. Потенциальную энергию при этом можно рассматривать в виде суммы двух слагаемых: Во многих случаях функция Для выполнения намеченной только что программы, необходимо, чтобы в области, где, в основном, движется электрон, удовлетворялось условие плавности
Если кристалл не кубический, то в качестве Другие условия применимости метода эффективной массы будут указаны ниже. Этот метод мы будем подробно рассматривать в последующем курсе «Введение в теорию полупроводников». Здесь мы сформулируем только окончательные результаты. Рассмотрим сначала поведение электронов вблизи дна невырожденной зоны с параболическим невырожденным законом дисперсии, т.е. когда закон дисперсии электрона можно представить в виде
где В этом случае волновую функцию электрона, движущегося в рассматриваемом силовом поле, можно представить в виде
Здесь
где
и
Как и следовало ожидать, здесь просто восстанавливается энергетический спектр электрона вблизи дна зоны. Уравнения (5) и формула (4) справедливы, если функция
где Аналогично обстоит дело и в случае электронов, движущихся у потолка зоны (по прежнему невырожденной и со скалярной эффективной массой). При этом эффективная масса
где При наличии магнитного поля уравнения (5) и (9) видоизменятся. Как известно, из электродинамики, магнитное поле можно описывать векторным потенциалом
Фигурирующий в (5) и (10) оператор импульса при этом принимает известный из квантовой механики канонический вид
Далее, к потенциальной энергии
Здесь Таким образом, вместо (5) и (9), имеем
и
Здесь Для вычисления различных средних значений также достаточно знать только сглаженные функции
Иначе говоря, Приведенные уравнения можно обобщить и на случай анизотропного параболического закона дисперсии, когда изоэнергетические поверхности вблизи дна зоны представляют собой эллипсоиды. Следует лишь заменить обратные эффективные массы тензором обратной эффективной массы. При этом первое слагаемое в левой части (5) примет вид В частности, в случае если оси координат совпадают с главными осями эллипсоида энергии, вместо (12) и (13) мы получим
и
В кристаллах с кубической системы анизотропия эффективной массы может иметь место, только в случае если минимум энергии расположен не в центре зоны Бриллюэна. При этом имеется несколько эквивалентных минимумов, соответствующих квазиимпульсам
где индекс Метод эффективной массы можно использовать и при непараболическом законе дисперсии. В этом случае оператор “кинетической энергии” Несколько более сложным является обобщение на случай вырожденных зон. Тогда нельзя ограничиваться только одной из них, поскольку условие (8) не выполняется. Физически это означает, что возмущение, описываемое потенциальной энергией
где индекс
Здесь Аналогично дело обстоит, если зоны не вырождены, но их края расположены близко друг к другу, так что в представляющей интерес области энергий условие (8) не выполняется (о таких зонах говорят как о “почти вырожденных”). Такой случай реализуется в полупроводниках с очень малой шириной зоны. Роль “почти вырожденных” здесь играют зона проводимости и валентная зона. При этом надо пользоваться не простыми равенствами (4) и (5), а более сложными (17) и (18).
Отметим, что деление на “невырожденные” и “почти вырожденные” зоны не является абсолютным. Как видно из предыдущего, оно определяется интервалом энергий, представляющих интерес. Ориентир здесь дает неравенство (8). Теперь рассмотрим вопрос о том, как наличие примесей сказывается на одноэлектронном спектре полупроводника. Для определенности рассмотрим донорную примесь. Если, например, в четырехвалентный Ge ввести пятивалентную примесь P, то четыре валентных электрона германия образуют ковалентные связи с 4-мя валентными электронами фосфора, а для пятого валентного электрона P нет пары, и он останется как бы лишним. Понятно, что за счет внешних воздействий (например, за счет тепловых колебаний кристаллической решетки) этот лишний 5-ый валентный электрон будет легко отщепляться от атома, становясь электроном проводимости. При этом в окрестности атома примеси образуется некомпенсированный положительный заряд. Таким образом, примесь Р превратиться в заряженный ион. Рассмотрим электрон проводимости в поле этого заряженного иона. Потенциальную энергию электрона в кристалле с примесью Поскольку сейчас нас интересует качественная картина трансформации спектра, то нам нужно сделать разумные приближения, которые позволили бы максимально упростить нашу задачу в вычислительном плане. При этом, конечно, наши упрощения не должны приводить к исчезновению качественного эффекта. Первое такое упрощение, которое кажется разумным для наших целей – это считать, что среднее расстояние электрона до примеси существенно больше межатомного расстояния. Тогда в первом приближении мы можем рассматривать движение электрона в непрерывной среде с диэлектрической проницаемостью
Тогда уравнение для огибающей принимает вид
и наша задача свелась к задаче об энергетическом спектре эффективной частицы с массой В области В области
Огибающая
где длина локализации
Таким образом, наличие примеси приводит к появлению в запрещенной зоне дискретных уровней энергии. Электрон, занимающий один из таких примесных уровней локализован вблизи атома примеси и в проводимости не участвует. Для того, чтобы получить электрон проводимости, нужно перевеси его из примесного уровня в непрерывным спектр (в зону проводимости). В рассмотренном нами случае так называемых мелких примесей уровни (23) расположены вблизи дна зоны проводимости, энергия ионизации В случае акцепторов ситуация гораздо сложнее. Валентность акцепторных примесей меньше, чем у основных атомов полупроводника. Поэтому когда мы помещаем акцепторную примесь в полупроводник, то у нас возникает неукомплектованная связь. Например, если мы Si будем легировать B, то трех валентных электронов бора не хватает для того, чтобы образовать ковалентные связи с четырьмя валентными атомами кремния, и одна ковалентная связь оказывается неукомплектованной. Электроны соседних атомов могут захватываться на эту связь. В результате примесь зарядится отрицательно, а по кристаллу будет кочевать вакантное место – дырка. Потенциал примеси искажает поле идеальной кристаллической решетки, и, соответственно, изменяет электронный спектр. Расчет таких примесных состояний гораздо сложнее, чем в случае доноров. В самом грубом приближении, гораздо более грубом, чем в случае доноров, мы можем рассмотреть электрон вблизи потолка валентной зоны в поле отрицательно заряженного иона. Уравнение Шредингера для огибающей электрона при этом имеет вид
Поскольку вблизи потолка зоны эффективная масса электрона отрицательная
Уравнение (23) совпадает с уравнением Шредингера для положительной частицы с зарядом Таким образом, акцепторные примеси приводят к появлению в запрещенной зоне дискретных уровней энергии. Когда ковалентная связь соседних атомов кремния разрывается и электрон из валентной зоны переходит на акцепторный уровень, в валентной зоне образуется вакантное место – дырка, которая при наложении электрического поля будет направлено перемещаться по кристаллу.
|
|||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 681; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.160.104 (0.015 с.) |

 имеет зонный характер, а одноэлектронный базис можно сформировать из блоховских волн
имеет зонный характер, а одноэлектронный базис можно сформировать из блоховских волн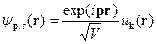 . (1)
. (1) . Здесь
. Здесь 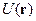 обозначает потенциальную энергию в идеальном кристалле, а
обозначает потенциальную энергию в идеальном кристалле, а 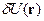 есть непериодическая функция, описывающая взаимодействие электрона с дефектом решетки. Также обстоит дело и при квантовомеханическом рассмотрении движения электрона в идеальном кристалле при наличии внешнего электрического поля.
есть непериодическая функция, описывающая взаимодействие электрона с дефектом решетки. Также обстоит дело и при квантовомеханическом рассмотрении движения электрона в идеальном кристалле при наличии внешнего электрического поля. . При этом задачу о движении электрона удобно решать с помощью приближенного приема, называемого методом эффективной массы. Идея его состоит в том, чтобы пользуясь плавностью функции
. При этом задачу о движении электрона удобно решать с помощью приближенного приема, называемого методом эффективной массы. Идея его состоит в том, чтобы пользуясь плавностью функции  . (2)
. (2)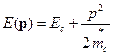 , (3)
, (3) - дно зоны проводимости,
- дно зоны проводимости,  - эффективная масса.
- эффективная масса. . (4)
. (4)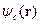 - нормированная функция Блоха, соответствующая дну рассматриваемой зоны, а
- нормированная функция Блоха, соответствующая дну рассматриваемой зоны, а  - «сглаженная» волновая функция. Уравнение для нее можно найти, подставляя выражение (4) в уравнение Шредингера с потенциальной энергией
- «сглаженная» волновая функция. Уравнение для нее можно найти, подставляя выражение (4) в уравнение Шредингера с потенциальной энергией  , (5)
, (5) - оператор квазиимпульса. Собственные значения уравнения (5) есть возможные значения энергии, отсчитанные от дна зоны
- оператор квазиимпульса. Собственные значения уравнения (5) есть возможные значения энергии, отсчитанные от дна зоны 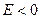 соответствует энергии, меньшей
соответствует энергии, меньшей  уравнение (5) дает
уравнение (5) дает . (6)
. (6) . (7)
. (7)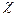 мало изменяется на протяжении постоянной решетки, а собственные значения энергии лежат достаточно близко к дну зоны проводимости. Именно, должно выполняться неравенство
мало изменяется на протяжении постоянной решетки, а собственные значения энергии лежат достаточно близко к дну зоны проводимости. Именно, должно выполняться неравенство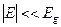 , (8)
, (8) - ширина запрещенной зоны, или, общее, расстояние от дна рассматриваемой зоны до ближайшего к нему края какой-либо другой зоны.
- ширина запрещенной зоны, или, общее, расстояние от дна рассматриваемой зоны до ближайшего к нему края какой-либо другой зоны. . Соответственно, аналог уравнения (5) имеет вид
. Соответственно, аналог уравнения (5) имеет вид , (9)
, (9) . Поскольку потенциальная энергия
. Поскольку потенциальная энергия 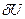 имеет электрическое происхождение, то изменение знака при ней можно интерпретировать как изменение знака заряда носителя. Иначе говоря, уравнение (9) описывает поведение дырки с положительной эффективной массой
имеет электрическое происхождение, то изменение знака при ней можно интерпретировать как изменение знака заряда носителя. Иначе говоря, уравнение (9) описывает поведение дырки с положительной эффективной массой 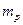 вблизи дна зоны проводимости вблизи дна дырочной (т.е. потолка валентной) зоны. Величина
вблизи дна зоны проводимости вблизи дна дырочной (т.е. потолка валентной) зоны. Величина  есть энергия дырки, отсчитываемая от потолка валентной зоны
есть энергия дырки, отсчитываемая от потолка валентной зоны  вниз. Отрицательные значения
вниз. Отрицательные значения  ) соответствуют энергии, большей
) соответствуют энергии, большей 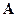 , удовлетворяющим условию
, удовлетворяющим условию . (10)
. (10) . (11)
. (11)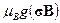 .
.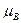 - магнетон Бора,
- магнетон Бора,  - гиромагнитное отношение. Для электронов и дырок в полупроводниках оно может отличаться от двух из-за спин-орбитального взаимодействия.
- гиромагнитное отношение. Для электронов и дырок в полупроводниках оно может отличаться от двух из-за спин-орбитального взаимодействия. (12)
(12) (13)
(13)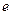 - абсолютная величина заряда электрона.
- абсолютная величина заряда электрона.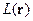 - любая функция, плавно изменяющаяся в пространстве, и пусть
- любая функция, плавно изменяющаяся в пространстве, и пусть  ,
, 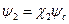 , где
, где  и
и  - решения уравнения (5). Тогда, как можно показать
- решения уравнения (5). Тогда, как можно показать . (14)
. (14) .
. (15)
(15) (16)
(16) (
( ). Уравнение (15) следует писать для каждого минимума в отдельности. Соответственно, получится столько (вообще говоря, различных) решений, сколько есть эквивалентных минимумов. Каждое такое решение имеет вид
). Уравнение (15) следует писать для каждого минимума в отдельности. Соответственно, получится столько (вообще говоря, различных) решений, сколько есть эквивалентных минимумов. Каждое такое решение имеет вид . (17)
. (17) нумерует минимумы, и под
нумерует минимумы, и под  следует понимать волновую функцию Блоха, отвечающую квазиимпульсу
следует понимать волновую функцию Блоха, отвечающую квазиимпульсу  в (12) и (13) приобретает вид
в (12) и (13) приобретает вид  , где
, где  . Уравнения (15) и (16) представляют собой частный случай этого общего правила.
. Уравнения (15) и (16) представляют собой частный случай этого общего правила. , (17)
, (17)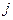 нумерует зоны, смыкающиеся в точке вырождения,
нумерует зоны, смыкающиеся в точке вырождения, 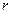 - число таких зон (кратность вырождения), а
- число таких зон (кратность вырождения), а  блоховская функция, соответствующая рассматриваемому краю
блоховская функция, соответствующая рассматриваемому краю  получается система
получается система  . (18)
. (18) - постоянные, определяющиеся структурой зон, и играющие ту же роль, что и компоненты тензора обратной эффективной массы для невырожденных зон. При
- постоянные, определяющиеся структурой зон, и играющие ту же роль, что и компоненты тензора обратной эффективной массы для невырожденных зон. При  мы можем представить в виде суммы потенциальной энергии в идеальной решетке
мы можем представить в виде суммы потенциальной энергии в идеальной решетке 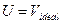 и дополнительного поля
и дополнительного поля  , обусловленного наличием примеси. Это дополнительное поле
, обусловленного наличием примеси. Это дополнительное поле  искажает спектр электрона в идеальной решетке. Наша задача сейчас состоит в том, чтобы понять как качественно изменяется этот спектр.
искажает спектр электрона в идеальной решетке. Наша задача сейчас состоит в том, чтобы понять как качественно изменяется этот спектр. . Поскольку среднее расстояние от электрона до иона существенно меньше, чем размер иона, то электрическое поле иона мы можем разложить по мультиполям. Для наших целей, естественно, разумно оставить только монопольный член. Таким образом, в наших приближениях движение электрона в поле иона сведется к его движению в кулоновском поле положительного точечного заряда
. Поскольку среднее расстояние от электрона до иона существенно меньше, чем размер иона, то электрическое поле иона мы можем разложить по мультиполям. Для наших целей, естественно, разумно оставить только монопольный член. Таким образом, в наших приближениях движение электрона в поле иона сведется к его движению в кулоновском поле положительного точечного заряда 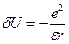 . (19)
. (19) , (20)
, (20)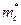 в кулоновском поле заряда
в кулоновском поле заряда 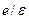 . С математической точки зрения уравнение (20) совпадает с уравнением для электрона в атоме водорода с той лишь разницей, что вместо массы истинной массы электрона в (20) фигурирует эффективная масса
. С математической точки зрения уравнение (20) совпадает с уравнением для электрона в атоме водорода с той лишь разницей, что вместо массы истинной массы электрона в (20) фигурирует эффективная масса 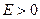 , т.е. энергий лежащих выше дна зоны проводимости, спектр является непрерывным. Огибающая функция
, т.е. энергий лежащих выше дна зоны проводимости, спектр является непрерывным. Огибающая функция  , т.е. ниже дна зоны проводимости, спектр является дискретным
, т.е. ниже дна зоны проводимости, спектр является дискретным (21)
(21) , (22)
, (22) получается указанной заменой из радиуса Бора
получается указанной заменой из радиуса Бора . (23)
. (23)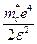 невелика. Поэтому при обычных условиях электроны забрасываются в зону проводимости и участвуют в явлениях переноса. Однако следует иметь в виду, что могут быть и глубокие примесные уровни (рассмотрение таких уровней в нашей простой модели невозможно), которые могут выступать в роли ловушек.
невелика. Поэтому при обычных условиях электроны забрасываются в зону проводимости и участвуют в явлениях переноса. Однако следует иметь в виду, что могут быть и глубокие примесные уровни (рассмотрение таких уровней в нашей простой модели невозможно), которые могут выступать в роли ловушек. , (23)
, (23)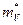 , то здесь удобно перейти к концепции дырки. Для этого нужно, формально умножить обе части уравнение (23) на -1. В
, то здесь удобно перейти к концепции дырки. Для этого нужно, формально умножить обе части уравнение (23) на -1. В , (23)
, (23) и энергией
и энергией  , которая движется в кулоновском поле отрицательного заряда
, которая движется в кулоновском поле отрицательного заряда  . Таким образом, в области
. Таким образом, в области  , т.е энергий, лежащих выше потолка запрещенной зоны, спектр является дискретным.
, т.е энергий, лежащих выше потолка запрещенной зоны, спектр является дискретным.


