Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эффективная масса электрона в кристаллеСодержание книги
Поиск на нашем сайте
Эффективная масса. Потенциальное поле решетки изменяет характер движения электрона в кристалле по сравнению с его движением в свободном пространстве. Поведение свободного электрона описывается волной де Бройля[9] и импульс электрона связан с волновым вектором соотношением
Если на электрон не действуют внешние силы, то его энергия не изменяется и, следовательно, сохраняется его состояние. Рассмотрим движение электрона в кристалле, на который действует внешняя сила
Ускорение электрона равняется
Воспользовавшись классическим законом сохранения энергии
Подстановка (4.37) в (4.39) приводит к выражению, аналогичному второму закону Ньютона[10]
если считать, что знаменатель дроби в выражении (4.40) имеет смысл массы электрона
Эта величина называется эффективной массой электрона и учитывает влияние периодической кристаллической решетки на движение электрона в кристалле под действием внешних сил. Эффективная масса не отражает ни инерциальных, ни гравитационных свойств электрона, а является некоторым удобным коэффициентом, с помощью которого можно рассматривать движение электрона в кристалле под действием внешней силы как свободного, то есть сложные законы движения электронов в кристалле свести к законам, которые по форме совпадают с законами классической механики. По величине эффективная масса может быть больше и меньше действительной массы электрона, а по знаку – положительной и отрицательной.
Форма изоэнергетической поверхности вблизи экстремальных точек Если рассматривать закон дисперсии Определим форму изоэнергетической поверхности вблизи экстремальных точек зоны, воспользовавшись решением (4.33). Для примитивных решеток с параметрами
Здесь учтено взаимодействие только с шестью ближайшими соседними атомами, то есть
получим
Представим
и для края зоны ((
Здесь коэффициенты
Для кристаллов, которые обладают кубической симметрией, все три главные оси эквивалентны и тензор обратной эффективной массы вырождается в скаляр Из (4.46) видно, что знак эффективной массы зависит от знака обменного интеграла Обменное взаимодействие сильнее для верхних энергетических зон в результате большего перекрывания волновых функций. Следовательно, эффективная масса, которая обратно пропорциональна обменному взаимодействию, будет уменьшаться с ростом номера зоны. Ширина разрешенных зон определяется разностью
Величина запрещенной зоны будет определяться разностью между минимальным и максимальным значениями энергии двух соседних зон (4.44 – 4.45), то есть в основном разностью соседних энергетических уровней электрона в изолированном атоме, которая уменьшается с увеличением энергии. Следовательно, с увеличением энергии ширина разрешенных зон увеличивается, а запрещенных зон уменьшается. Как видно из (4.44 – 4.45), закон дисперсии носит квадратичный характер, отклонения от него обусловлены необходимостью учета более высоких степеней разложения Понятие о дырках. В электрическом поле
Для электрона, который находится вблизи потолка энергетической зоны, эффективная масса отрицательна
Следовательно, такой носитель заряда ведет себя как частица с положительным зарядом и положительной эффективной массой. Запишем выражение для плотности тока, создаваемого электронами почти заполненной зоны
где Ток, который переносится электронами полностью заполненной зоны, равняется нулю, потому что средняя скорость электронов для такой зоны равняется нулю. Поэтому (4.50) можно переписать в эквивалентной форме
Следовательно, ток, создаваемый электронами, которые заполняют определенную совокупность состояний в зоне, эквивалентный току, который могли бы создать частицы с положительным зарядом Перечислим физические свойства дырки. Заряд дырки равняется по величине и противоположен по знаку заряду электрона. Эффективная масса дырки равняется по величине эффективной массе электрона в соответствующем незаполненном состоянии, но противоположна по знаку. Скорость дырки
Основным энергетическим состоянием для дырки является состояние возле потолка зоны, возбуждение дырки отвечает ее движение вниз по энергетической зоне.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 395; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.0.48 (0.006 с.) |

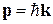 . Поэтому закон дисперсии для свободного электрона носит квадратичный характер
. Поэтому закон дисперсии для свободного электрона носит квадратичный характер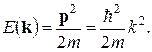 (4.36)
(4.36)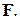 Скорость электрона связана с энергией соотношением
Скорость электрона связана с энергией соотношением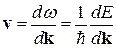 . (4.37)
. (4.37)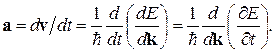 (4.38)
(4.38)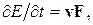 получим
получим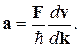 (4.39)
(4.39)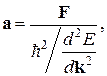 (4.40)
(4.40)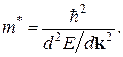 (4.41)
(4.41)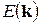 в
в  -пространстве, то уравнение
-пространстве, то уравнение 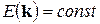 определяет в этом пространстве некоторую поверхность, которая называется изоэнергетической поверхностью или поверхностью постоянной энергии. Форма этой поверхности, которая зависит от энергетического спектра электрона в кристалле, определяет многие физические свойства металлов и полупроводников.
определяет в этом пространстве некоторую поверхность, которая называется изоэнергетической поверхностью или поверхностью постоянной энергии. Форма этой поверхности, которая зависит от энергетического спектра электрона в кристалле, определяет многие физические свойства металлов и полупроводников.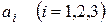 выражение (4.33) можно привести к виду
выражение (4.33) можно привести к виду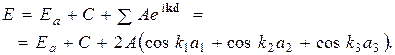 (4.42)
(4.42)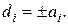 Так как
Так как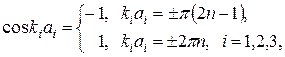
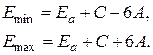 (4.43)
(4.43)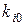 первой зоны Бриллюэна. Ввиду того, что в экстремуме
первой зоны Бриллюэна. Ввиду того, что в экстремуме 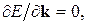 то, используя разложение косинуса по малому параметру, получим из (4.42) для центра зоны (
то, используя разложение косинуса по малому параметру, получим из (4.42) для центра зоны (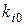 =0)
=0)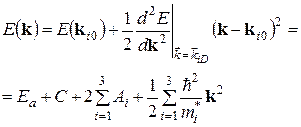 (4.44)
(4.44)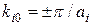 )
)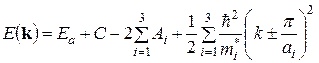 . (4.45)
. (4.45)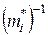 представляют собой диагональные элементы тензора обратной эффективной массы
представляют собой диагональные элементы тензора обратной эффективной массы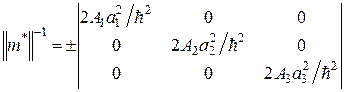 (4.46)
(4.46) .
.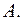 При
При 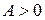 в точках
в точках 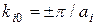 минимум энергии и эффективная масса положительная. При
минимум энергии и эффективная масса положительная. При 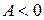 в точках
в точках 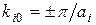 находится максимум энергии и
находится максимум энергии и  а в точках
а в точках 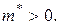
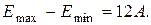 (4.47)
(4.47)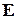 на электрон действует сила, равная
на электрон действует сила, равная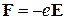 . (4.48)
. (4.48)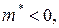 и ускорение, обусловленное внешней силой, будет равняться
и ускорение, обусловленное внешней силой, будет равняться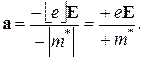 (4.49)
(4.49)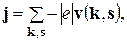 (4.50)
(4.50)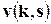 — скорость электрона с волновым вектором
— скорость электрона с волновым вектором 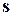 . Суммирование проводится по всем заполненным состояниям зоны Бриллюэна.
. Суммирование проводится по всем заполненным состояниям зоны Бриллюэна.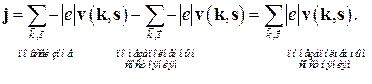 (4.51)
(4.51)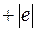 при заполнении ими вакантных состояний. Таким образом, хотя единственными реальными носителями заряда являются электроны, в некоторых случаях для удобства можно считать, что ток полностью переносится положительными частицами, которые заполняют все те состояния в зоне, которые не заняты электронами. Такие фиктивные частицы называют дырками.
при заполнении ими вакантных состояний. Таким образом, хотя единственными реальными носителями заряда являются электроны, в некоторых случаях для удобства можно считать, что ток полностью переносится положительными частицами, которые заполняют все те состояния в зоне, которые не заняты электронами. Такие фиктивные частицы называют дырками.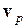 равняется скорости
равняется скорости 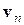 отсутствующего электрона, а волновой вектор дырки
отсутствующего электрона, а волновой вектор дырки 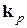 и квазиимпульс
и квазиимпульс 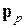 имеют противоположные волновому вектору
имеют противоположные волновому вектору 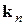 и квазиимпульса
и квазиимпульса 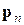 электрона знаки
электрона знаки