
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энергетические состояния в несовершенных кристаллахСодержание книги
Поиск на нашем сайте
Используемые в электронике кристаллы далеки от структурного совершенства. У них существуют различные дефекты, представляющие собой отклонения от правильного расположения атомов, либо включения посторонних атомов в кристаллическую решетку. Дефекты могут возникать как в результате преднамеренного воздействия на кристалл, так и случайно, под действием неконтролируемых факторов. Рассмотрим, как дефекты влияют на электронные свойства кристалла. Примесные уровни. Очевидно, что энергетические уровни электронов примесных атомов могут не совпадать с энергетическими уровнями электронов атомов матрицы. При этом они могут располагаться как в одной из разрешенных зон (что обычно не представляет интереса), так и в запрещенной зоне. При большой концентрации примесных атомов соответствующие им уровни могут образовать даже дополнительную зону. Дополнительные уровни возникают не по всей решетке, а только в местах расположения примесей. Поэтому такие уровни называют локальными. В пространстве примесные атомы обычно располагаются далеко друг от друга и переходы электронов между ними невозможны. Предположим, что один из узлов в кристалле четырехвалентной матрицы (например, кремния или германия) замещен атомом примеси, имеющим пять валентных электронов (например, мышьяка). Четыре из них будут участвовать в образовании ковалентной связи с ближайшими соседними атомами матрицы. Пятый электрон, не принимая участия в обменной связи, будет взаимодействовать с большим количеством атомов матрицы, и в результате его связь с ионом примеси оказывается сильно ослабленной. Для определения энергетического спектра такого электрона можно использовать так называемый метод эффективной массы. Суть его заключается в следующем. Уравнение Шредингера для не задействованного на связи электрона примесного атома имеет вид
где Непосредственное решение этого уравнения затруднено в связи с тем, что нам неизвестен потенциал
где
В выражение для потенциальной энергии
Соотношение (4.58) справедливо в том случае, когда расстояние между взаимодействующими зарядами достаточно большое, то есть орбита электрона примесного атома должна охватывать большое число узлов кристаллической решетки. В этом случае воздействие атомов матрицы на электрон учитывается интегральным коэффициентом Решение уравнения (4.56) проводится по аналогии с уравнением для атома водорода, и для собственных значений энергии получаем выражение
где Перепишем (4.59) следующим образом:
где
Из (4.60) следует, что энергетический уровень основного состояния
Рассмотрим в качестве примера германий. Взяв для массы проводимости Радиус орбиты электрона примесного атома из расчетов по водородоподобной модели равен
где Для германия радиус орбиты электрона при Из аналогичных расчетов для трехвалентных (акцепторных) примесей можно сделать вывод, что уровни акцепторной примеси лежат в запрещенной зоне выше потолка валентной зоны и имеют энергию ионизации такого же порядка, как и донорные (рис. 4.13, б).
Получены экспериментальным путем энергии ионизации примесей некоторых элементов приведены в табл. 4.2.
Примеси I, II, VI и VIII групп, имеющие энергию ионизации сравнимую с шириной запрещенной зоны, образуют глубокие уровни. Причем та же примесь может образовывать как донорные, так и акцепторные уровни. Такие примеси называют амфотерными. Например, золото в германии образует донорный уровень Не только примеси, но и собственные дефекты кристаллической решетки (вакансии, межузельные атомы и т.д.) могут создавать локальные состояния в запрещенной зоне.
Таблица 4.2. Энергия ионизации примесей элементов III и V групп в германии и кремнии
Уровни Тамма [12]. Кристаллы имеют конечную протяженность, и наличие поверхности нарушает строгую периодичность атомов. Это приводит к изменению зонной структуры вблизи поверхности кристалла и появлению локальных (поверхностных) уровней в запрещенной зоне. И.Е.Тамм впервые показал, что наличие границы должно приводить к появлению в запрещенной зоне кристалла разрешенных энергетических состояний. Он воспользовался моделью Кронига-Пенни, но оборвал поле с одной стороны введением порога Для бесконечного кристалла коэффициент
Здесь
Следовательно, уравнение (4.24) принимает вид
А так как Этим корням отвечают поверхностные уровни, которые получили наименование уровней Тамма. Они не являются дополнительными к числу уровней, содержащихся в разрешенных зонах, а представляют собой уровни, отщепившиеся от соответствующих разрешенных зон. В трехмерном кристалле уровни Тамма расщепляются в приповерхностную зону, причем волновые функции электронов, которые находятся на приповерхностных уровнях, спадают экспоненциально от границы кристалла, так что электроны могут удалиться от границы не более чем на величину постоянной решетки. Концентрация уровней Тамма определяется поверхностной концентрацией атомов кристалла и составляет величину примерно К образованию поверхностных состояний приводит также наличие нескомпенсированных валентных связей у атомов на границе решетки (уровни Шокли [13]). Плотность уровней Шокли, как и уровней Тамма, определяется концентрацией поверхностных атомов. В реальных кристаллах основную роль играют уровни, связанные с искажением потенциала решетки у границы за счет адсорбированных на поверхности атомов или дефектов поверхности, образованных в процессе технологической обработки кристалла. При больших концентрациях дефектов поверхностные уровни расщепляются с образованием поверхностной энергетической зоны.
Ловушки. Зонные диаграммы реальных кристаллов содержат большое число локальных энергетических уровней в запрещенной зоне, связанных с дефектами решетки, которые способные захватывать электроны и дырки и выводить их из процесса электропроводности. Ловушки электронов вблизи дна зоны проводимости и дырок вблизи потолка валентной зоны называют центрами (уровнями) захвата. При слабых тепловых возбуждениях они могут неоднократно обмениваться носителями заряда с соответствующей зоной. Наряду с центрами захвата имеются уровни, расположенные ближе к середине запрещенной зоны, способные длительное время удерживать электроны – до момента их рекомбинации с дырками. Электрон зоны проводимости, захваченный такой ловушкой, через какое-то время может перейти на свободный уровень валентной зоны. Таким образом, ловушка служит центром рекомбинации электронов и дырок (рис. 4.14 а). Центры окраски и люминесценции. Дефекты решетки в ионных кристаллах, связанные с появлением вакансий положительных или отрицательных ионов, вызывают местное нарушение электронейтральности и создают избыток положительного или отрицательного заряда в месте образования вакансии. Если вакансии захватывают электроны или дырки, они приобретают способность поглощать и называются центрами окраски. Электрон, захваченный анионной вакансией в щелочно-галоидном кристалле, называется F-центром (от немецкого Farbzentrum – центр окраски) (рис.4.14 б). Благодаря наличию F-центров кристалл NaCl окрашивается в желтовато-коричневый, а KCl – в голубой цвет. Поглощение кристалла, содержащего центры окраски, наблюдается в полосе длин волн, которая может иметь ширину порядка 20 нм.
В F΄-центрах вакантный узел захватывает два электрона. Существует также аналог F-центра, образующийся при избытке атомов Cl в кристалле NaCl. Прогревание соли в парах галоидов вызывает появление вакантных катионных узлов, способных захватить дырки и образовать V-центры. Они не настолько стойкие как F-центры и исчезают при комнатной температуре. Центры окраски появляются в результате нарушения стехиометрического состава, который может возникать не только за счет избытка одной из компонентов, но и под действием рентгеновского излучения,
Наличие примесей в солях обуславливает также явление люминесценции, которое состоит в возникновении вторичного излучения после поглощения света. Если вторичное излучение происходит непосредственно при облучении, то есть с задержкой порядка
Таблица 4.3. Энергия поглощения F-центров (максимальные значения) щелочно-галоидных соединений
Люминесценция протекает следующим образом. Когда примесный ион возбуждается поглощенным фотоном, его размер в кристалле изменяется, что приводит к изменению положений соседних ионов. Так как соседние ионы переместились в другие положения, энергия возбужденного состояния адиабатически снижается и при этом в течение очень короткого времени испускается вторичный фотон. Однако в момент излучения фотона возбужденное состояние имеет меньшую энергию, чем в момент поглощения первичного фотона, поэтому испущенный фотон имеет меньшую частоту, чем поглощенный. Таким образом, кристалл, поглощающий УФ-излучение, может испускать видимый свет. Экситоны. Под экситоном понимают электрически нейтральное электронное нарушение (квазичастицу) в кристалле диэлектрика или полупроводника, мигрирующее в кристалле, но не связанное с переносом электрического заряда и массы. Понятие об экситоне было введено Я.И.Френелем в 1931 г. В молекулярных кристаллах, в которых взаимодействие между отдельными молекулами слабее, чем взаимодействие между атомами и электронами внутри молекулы, возникающее электронное возбуждение отдельной молекулы распространяется в кристалле в виде волны (за счет межмолекулярного взаимодействия переходит от одной молекулы к другой). Такое нарушение называется экситоном Френкеля, оно сосредоточено в пределах одного узла решетки, и поэтому для описания экситонного состояния можно пользоваться волновыми функциями изолированных атомов или молекул. Экситон Ванье [14] -Мотта [15], наблюдаемый в полупроводниках, представляет собой водородоподобное связанное состояние электрона проводимости и дырки. Энергии связи
где Расчеты показывают, что радиус экситона Ванье-Мотта в много раз больше межатомного расстояния кристалла, поэтому экситон является макроскопическим образованием. Для Ge, Si и полупроводников типа
При малых концентрациях экситоны ведут себя в кристалле подобно газу. При больших концентрациях становится существенным их взаимодействие и возможно образование связанного состояния двух экситонов – экситонной молекулы (биэкситоны). При некоторой критической концентрации в полупроводнике происходит «сжижение» экситонного газа – образование электронно-дырочной фазы, обладающей металлическими свойствами. В процессе хаотического перемещения в кристалле экситон может взаимодействовать с другими квазичастицами или дефектами. При этом изменяется его энергия и импульс, что приводит либо к образованию свободного электрона и дырки, либо к излучению фотона. Эффективная масса, соответствующая движению экситона как целого, составляет Экситонные уровни заметно влияют на спектр поглощения, а также на процессы, связанные с переносом энергии возбуждения в кристалле. Поляроны. Движущийся по кристаллу электрон (или дырка) своим полем смещает ионы кристаллической решетки и тем самым деформирует и поляризует ее. Деформация решетки приводит к образованию потенциальной ямы, которая захватывает и удерживает породивший ее носитель заряда. Перемещающееся как единое целое носитель заряда и потенциальная яма представляют квазичастицу – полярон. Энергия полярона квантована, а энергетические уровни находятся в запрещенной зоне. Полярон является носителем заряда с большой эффективной массой, в сотни раз большей массы электрона. Поскольку энергия полярона меньше энергии свободного электрона в среде, где отсутствует поляризация, в ряде веществ, например в окислах переходных металлов и полупроводниках с узкой зоной проводимости, электроны проводимости находятся в поляроном состоянии. Поляроны, созданные электроном и дыркой, могут объединяться в систему из двух связанный поляронов – «поляронный» экситон. Плазмоны. Это квазичастицы, которые описывают коллективные колебания электронов проводимости вокруг тяжелых ионов в плазме, в частности в плазме твердого тела. Частота основной моды плазменных колебаний – плазменная частота
и уравнение движения электрона в плазме может быть записано в виде
и, следовательно, для резонансной (плазменной) частоты получим
Частота колебаний зависит от геометрической формы образца, но если длина волны плазмона становится малой по сравнению с размерами образца, то влияние формы исчезает. Концентрация электронов в полупроводниках и металлах изменяется в широких пределах, поэтому энергия плазмона Высокие значения энергии плазмонов обусловлены тем, что плазменные колебания представляют собой результат коррелированного движения большого числа электронов. В полупроводниках возможное появление двух мод плазменных колебаний, одна из которых (высокочастотная) определяется колебаниями валентных электронов, а другая (низкочастотная) колебаниями электронов зоны проводимости. Плазмоны играют большую роль в оптических свойствах металлов. Свет с частотой ниже плазменной частоты отражается, потому что электроны экранируют электрическое поле световой волны. Свет с частотой выше плазменной частоты проходит. В металлах плазменная частота лежит в ультрафиолетовой области спектра, делая их блестящими в видимом диапазоне. Плазмон может взаимодействовать с фотоном, образуя квазичастицу – поляритон. Вдоль границы металла могут возбуждаться и распространяться поверхностные плазмоны с энергией, меньше, чем у объемных плазмонов. Поверхностные плазмоны полностью локализуются на поверхности. Поверхностный плазмонный резонанс может быть использован для оптической обработки сигналов, поверхностной спектроскопии и сенсорной нанотехнологии. Он используется для получения информации о диэлектрической проницаемости и толщине непроводящего слоя окисла, покрывающего металл, в биохимии для определения присутствия молекул на поверхности.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 417; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.82.70 (0.01 с.) |

 (4.55)
(4.55) – периодический потенциал поля решетки,
– периодический потенциал поля решетки,  – потенциальная энергия взаимодействия электрона с ионом примеси.
– потенциальная энергия взаимодействия электрона с ионом примеси. (4.56)
(4.56) есть омическая эффективная масса (или эффективная масса проводимости) и которая определяется как среднеарифметическое от компонентов тензора обратной эффективной массы:
есть омическая эффективная масса (или эффективная масса проводимости) и которая определяется как среднеарифметическое от компонентов тензора обратной эффективной массы: . (4.57)
. (4.57) , тем самым учитывается то обстоятельство, что движение электрона происходит в твердом теле вокруг иона с зарядом
, тем самым учитывается то обстоятельство, что движение электрона происходит в твердом теле вокруг иона с зарядом  :
: . (4.58)
. (4.58) .
. , (4.59)
, (4.59)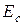 – энергия, соответствующая дну зоны проводимости,
– энергия, соответствующая дну зоны проводимости,  .
. (4.60)
(4.60) или в единицах СИ
или в единицах СИ  . (4.61)
. (4.61) донорной примеси находится в запрещенной зоне на расстоянии
донорной примеси находится в запрещенной зоне на расстоянии  от дна зоны проводимости (рис. 4.13, а). Подставив значение постоянных в (4.61), получим
от дна зоны проводимости (рис. 4.13, а). Подставив значение постоянных в (4.61), получим эВ. (4.62)
эВ. (4.62)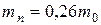 и для
и для  получим величину энергии ионизации примесных пятивалентных атомов порядка
получим величину энергии ионизации примесных пятивалентных атомов порядка  эВ.
эВ. (4.63)
(4.63) нм — радиус первой боровской орбиты атома водорода.
нм — радиус первой боровской орбиты атома водорода. составит
составит  нм. Постоянная решетки германия равна
нм. Постоянная решетки германия равна  нм, следовательно, орбита электрона охватывает приблизительно 103 атомов, что подтверждает возможность использования макроскопического параметра
нм, следовательно, орбита электрона охватывает приблизительно 103 атомов, что подтверждает возможность использования макроскопического параметра  при рассмотрении движения электрона в кристалле.
при рассмотрении движения электрона в кристалле.

 эВ, акцепторные одно- и двукратно заряженные уровни с энергиями соответственно
эВ, акцепторные одно- и двукратно заряженные уровни с энергиями соответственно 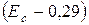 эВ и
эВ и  эВ.
эВ.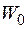 (учет вакуума).
(учет вакуума). (квазиволновое число) в уравнении Кронига-Пенни (4.24) может быть только действительным. Если вводится граница, то
(квазиволновое число) в уравнении Кронига-Пенни (4.24) может быть только действительным. Если вводится граница, то  (4.64)
(4.64) взято для упрощения анализа. В этом случае для правой части (4.24) получаем
взято для упрощения анализа. В этом случае для правой части (4.24) получаем
 . (4.65)
. (4.65) , то это означает, что корни уравнения появляются и в запрещенной зоне.
, то это означает, что корни уравнения появляются и в запрещенной зоне. . В зависимости от места расположения на энергетической диаграмме они проявляют себя как уровни доноров, акцепторов или центров рекомбинации.
. В зависимости от места расположения на энергетической диаграмме они проявляют себя как уровни доноров, акцепторов или центров рекомбинации.

 -лучей и др. Концентрация центров окраски может достигать
-лучей и др. Концентрация центров окраски может достигать  м-3. Они определяют полосы поглощения света в видимой (F-центры) и ультрафиолетовой (V-центры) областях спектра. Значения энергии максимумов полос поглощения F-центров некоторых кристаллов приведены в табл. 4.3.
м-3. Они определяют полосы поглощения света в видимой (F-центры) и ультрафиолетовой (V-центры) областях спектра. Значения энергии максимумов полос поглощения F-центров некоторых кристаллов приведены в табл. 4.3. с, то процесс излучения называется флуоресценцией. При задержке более
с, то процесс излучения называется флуоресценцией. При задержке более  с имеет место фосфоресценция.
с имеет место фосфоресценция. и эффективные радиусы
и эффективные радиусы  экситона Ванье-Мотта можно оценить по формулам Бора для атома водорода, учитывая эффективные массы электронов проводимости
экситона Ванье-Мотта можно оценить по формулам Бора для атома водорода, учитывая эффективные массы электронов проводимости  и дырок
и дырок  и диэлектрическую проницаемость полупроводника
и диэлектрическую проницаемость полупроводника  эВ, (4.66)
эВ, (4.66) см, (4.67)
см, (4.67) – приведенная масса экситона,
– приведенная масса экситона,  – масса электрона.
– масса электрона. и
и  размер экситона порядка
размер экситона порядка  эВ. Энергетический спектр экситона подобен спектру атома водорода (рис.4.15).
эВ. Энергетический спектр экситона подобен спектру атома водорода (рис.4.15).
 , время жизни
, время жизни  экситона невелико: электрон и дырка рекомбинируют с излучением фотона за время
экситона невелико: электрон и дырка рекомбинируют с излучением фотона за время  с. Кроме того, экситон может погибнуть безизлучательно, например, при захвате дефектами решетки.
с. Кроме того, экситон может погибнуть безизлучательно, например, при захвате дефектами решетки. – может быть вычислена из следующих соображений. Если в результате каких-либо флуктуаций электроны с концентрацией
– может быть вычислена из следующих соображений. Если в результате каких-либо флуктуаций электроны с концентрацией  будут смещены на расстояние
будут смещены на расстояние  относительно решетки, то диэлектрическая поляризация составит
относительно решетки, то диэлектрическая поляризация составит  . Величина деполяризующего поля, которое стремится возвратить электронный газ в равновесное состояние относительно ионов, будет
. Величина деполяризующего поля, которое стремится возвратить электронный газ в равновесное состояние относительно ионов, будет
 , (4.68)
, (4.68) . (4.69)
. (4.69) для различных твердых тел лежит в пределах
для различных твердых тел лежит в пределах  эВ. Следовательно, тепловое возбуждение плазменных колебаний невозможно. Для их возникновения необходимое проникновение в решетку электронов высоких энергий, каждый из которых, двигаясь в кристалле, может последовательно возбуждать несколько плазмонов.
эВ. Следовательно, тепловое возбуждение плазменных колебаний невозможно. Для их возникновения необходимое проникновение в решетку электронов высоких энергий, каждый из которых, двигаясь в кристалле, может последовательно возбуждать несколько плазмонов.


