
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энергетическая структура твердых телСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ЭНЕРГЕТИЧЕСКАЯ СТРУКТУРА ТВЕРДЫХ ТЕЛ Дискретные энергетические уровни атомов, образующих твердое тело, под действием возмущающего действия полей окружающих атомов расщепляются в энергетические зоны. Решение уравнения Шредингера в приближении сильной или слабой связи дает качественно одну и ту же картину для структуры энергетических зон твердых тел. Наибольшее значение для электронных свойств твердых тел имеют верхняя и расположенная ниже разрешенные зоны энергий. Если между ними нет энергетического зазора, то твердое тело с такой зонной структурой является металлом. Если величина энергетической щели между этими зонами (запрещенной зоны) больше 3 эВ, то твердое тело является диэлектриком. И, наконец, если ширина запрещенной зоны составляет (0,1 ÷ 3,0) эВ, то твердое тело принадлежит к классу полупроводников. Поскольку в полупроводниках ширина запрещенной зоны меняется в широком диапазоне, то вследствие этого в значительной мере меняется их удельная проводимость. Рассматриваются энергетические состояния в несовершенных кристаллах, вводится понятие энергии Ферми в металлах, уровня Ферми в полупроводниках. Метод сильной связи
Для расчета зонной структуры глубоких энергетических уровней используют метод сильной связи, предложенный Блохом. В нем предполагается, что энергия электрона в изолированном атоме мало изменяется при конденсации атомов в кристалл. Используя метод возмущений, в качестве нулевого приближения выбираем состояние электрона в кристалле из невзаимодействующих атомов, которое описывается уравнением Шредингера
где
Решение уравнения (4.27) для изолированного атома известно, а влияние периодического поля на движение электрона и взаимодействие между атомами можно принять как возмущение. Тогда уравнение Шредингера
будет иметь гамильтониан вида
где В качестве нулевого приближения для волновой функции выбираем линейную комбинацию атомных волновых функций
причем из условия периодичности следует, что
Воспользовавшись (4.30), (4.31) и условием нормирования для волновых функций, преобразуем (4.32) к следующему виду
где
Выражение (4.34) определяет усредненную для некоторого атома потенциальную энергию электрона в поле всех других ядер и электронов; интеграл (4.35) характеризует обменное взаимодействие между парой каких-либо атомов, которые находятся на расстоянии Таким образом, на основании (4.33) можно сделать вывод, что каждое атомное состояние превращается в разрешенную энергетическую зону и энергетический уровень размывается в полосу, ширина которой пропорциональна
Таблица 4.1. Значение безразмерных постоянных
Эффективные массы тяжелых и легких дырок равны соответственно Для третьей полосы вырождение частично снимается за счет спин-орбитального расщепления, обусловленного взаимодействием спина электрона с магнитным полем орбитального движения, в результате чего ветвь опускается на величину Ширина запрещенной зоны в различных точках зоны Бриллюэна разная. Однако под шириной запрещенной зоны принято понимать минимальное расстояние между дном зоны проводимости и потолком валентной зоны. При абсолютном нуле температуры ширина запрещенной зоны равняется 1,21 эВ для кремния и 0,78 эВ для германия. При увеличении температуры ширина запрещенной зоны убывает приблизительно по линейному закону с коэффициентом
где Полупроводниковые соединения типа Ширина запрещенной зоны при комнатной температуре и нормальном атмосферном давлении составляет у арсенида галлия – Интересной особенностью арсенида галлия является наличие локального минимума энергии (верхней долины), расположенной на
Малая кривизна дисперсионной кривой в верхней долине обусловливает большую величину эффективной массы электрона Металлы. Если разрешенная зона заполнена не полностью, то электроны могут ускоряться и переходить под действием электрического поля на свободные состояния в пределах одной зоны. В этом случае мы имеем дело с типичным металлом или проводником. Металлическая проводимость образуется и при перекрывании заполненной энергетической зоны с незаполненной зоной (рис. 4.7 в, г). Число состояний в зоне определяется как Нечетное число электронов, приходящихся на элементарную ячейку (Al, In и др.), также приводит к частичному заполнению энергетической зоны, что обеспечивает металлические свойства. Однако в некоторых случаях, когда вещество кристаллизируются в структуре с двумя или больше атомами в элементарной ячейке (As, Sb, Bi и др.) возникает ситуация, близкая к полупроводниковой проводимости. Такие вещества называют полуметаллами. Зонную структуру их можно рассматривать, как и для полупроводников, однако минимум зоны проводимости лежит немного ниже максимума валентной зоны, то есть разрешенные энергетические зоны перекрываются, и понятие запрещенной зоны теряет смысл.
Плотность состояний в обоих случаях (4.105) и (4.106) имеет одинаковый вид, расхождение лишь в знаке подкоренного выражения, что обусловливается разными знаками эффективной массы у дна и потолка зоны. Таким образом, эллипсоидальные изоэнергетические поверхности вблизи экстремальных точек зоны проводимости и валентной зоны можно заменить сферическими поверхностями, для которых эффективная масса имеет вид (4.108), что является удобным при конкретных вычислениях. Рассмотрим кремний (рис.4.11, б). Он имеет шесть минимумов (М=6) в зоне проводимости, расположенных по направлениям <100> на расстоянии
Валентная зона кремния в k=0 дважды вырождена и изоэнергетические поверхности имеют сложный вид, однако их можно аппроксимировать двумя сферическими поверхностями, которым соответствуют легкие
При соответствующих расчетах для германия стоит учесть то обстоятельство, что минимумы зоны проводимости располагаются на границе первой зоны Бриллюэна по направлениям <111> (рис.4.11, а). Поэтому восемь эллипсоидов равных энергий рассечены пополам границами зоны Бриллюэна и эффективная масса плотности состояний в зоне проводимости будет равна
Здесь учтено, что ml= 1,64 m и mt= 0,082 m. Валентная зона имеет вырожденный максимум при k=0 и характеризуется наличием легких и тяжелых дырок, и соответствующая зоне эффективная масса плотности состояний будет равна
Закон действующих масс
В примесном полупроводнике имеются основные и неосновные носители заряда. Для полупроводника n-типа (электронного) основными являются электроны, а дырки – неосновными. Для полупроводника р-типа ( дырочного) основными являются дырки, электроны – неосновными. В полупроводнике равновесная концентрация электронов в зоне проводимости определяется выражением (4.115), а дырок в валентной зоне – (4.116). Перемножив эти выражения, получим
Обозначим концентрации: электронов
Соотношение (4.134) называется законом действующих масс: для данной температуры произведение равновесных концентраций основных и неосновных носителей заряда есть величина постоянная и равная квадрату концентрации собственных носителей. Выражение (4.134) обычно используют для определения концентрации неосновных носителей заряда. Вырожденные полупроводники. Степень вырожденности полупроводника определяется положением уровня Ферми. Для ее оценки удобно пользоваться величиной приведенного уровня Ферми. Концентрацию электронов в зоне проводимости, используя (4.76) и безразмерные параметры
можно представить в виде
где
называется интегралом Ферми. Величина h называется приведенным уровнем Ферми. При
что соответствует статистике Больцмана, и, следовательно, полупроводник является невырожденным. Условие
и равновесная концентрация электронов в вырожденном донорном полупроводнике определяется из (4.136)
где При условии
Контрольные вопросы и задачи
1. В чем суть адиабатического и одноэлектронного приближения при решении уравнения Шредингера для электронов в кристалле? 2. Что такое идеальная кристаллическая решетка и как она влияет на движение электрона в кристалле? 3. В чем сущность модели Кронига-Пенни? 4. Что такое зона Бриллюэна? 5. Чем определяется число уровней в энергетической зоне? 6. Эффективная масса электрона в кристалле и ее физическая суть. 7. Что такое дырка с точки зрения зонной теории? 8. Понятие полупроводника, металла и диэлектрика в зонной теории. 9. Что такое водородоподобная модель примесного состояния? 10. Как возникают уровни Тамма? 11. Что собой представляют экситоны? 12. Что такое энергия Ферми и как она зависит от концентрации электронов в металле? 13. Рассчитайте энергию Ферми при 14. Определить температуру Ферми и фермиевскую скорость электронов для меди, которая является одновалентным металлом (предполагая, что 15. В полупроводнике ZnSb ширина запрещенной зоны – энергию ионизации доноров; – радиус орбиты электрона в основном состоянии; – при какой минимальной концентрации доноров станут заметны эффекты, связанные с перекрытием орбит соседних примесных атомов?
Литература к главе
1. Фридрихов, С.Ф. Физические основы электронной техники [Текст]: учеб. / С.Ф. Фридрихов, С.М. Мовнин. – М.: Высш. школа, 1982. – 608 с. 2. Епифанов, Г.И. Физика твердого тела [Текст]: учеб. пособие / Г.И.Епифанов. – М.: Высш. школа, 1977. – 288 с. 3. Шалимова, К.В. Физика полупроводников [Текст]: учеб. пособие / К.В.Шалимова. – М.: Энергия, 1971. – 312 с. 4. Черняков, Е.І. Фізика твердого тіла [Текст]: навч. посібник/ Е.І. Черняков, О.С.Замковий, Г.Г.Канарик. – Харків: Колегіум, 2006. – 264 с.
[1] Георг Симон Ом (нем. Georg Simon Ohm; 1787 – 1854) – знаменитый немецкий физик. Установил основной закон электрической цепи (закон Ома). Труды по акустике, кристаллооптике. [2] Джеймс Прескотт Джоуль (англ. James Prescott Joule; 1818- 1889) – английский физик. Джоуль изучал природу тепла и обнаружил её связь с механической работой, открыл связь между током, текущим через проводник с определённым сопротивлением, и выделяющимся при этом теплом (закон Джоуля). [3] Эмилий Христианович Ленц (нем. Heinrich Friedrich Emil Lenz; 1804 – 1865) – знаменитый русский физик. Главнейшие результаты его исследований: закон индукции (правило Ленца), закон Джоуля-Ленца, опыты, подтверждающие явление Пельтье.
[4]Матиссен Огастес (1831–1870) – английский физик. [5] Уильям Роуэн Гамильтон (англ. William Rowan Hamilton; 1805 –1865) – выдающийся ирландский математик и физик XIX века. Оба главных открытия Гамильтона – новая формулировка механики и кватернионы –сыграли существенную роль в XX веке при возникновении квантовой механики. [6] Феликс Блох (нем. Felix Bloch; 1905 –1983) – швейцарский физик, работавший главным образом в США. Лауреат Нобелевской премии по физике за 1952 год (совместно с Эдвардом Пёрселлом). Работы посвящены физике твердого тела, магнетизму, квантовой электродинамике, сверхпроводимости, ядерной физике. Заложил (совместно с Л. Бриллюэном) основы зонной теории твердых тел (1928) и низкотемпературного ферромагнетизма. Известен также формулой Бете – Блоха для тормозной способности, теоремой Блоха в теории сверхпроводимости, теоремой Блоха–Нордсека в квантовой электродинамике, уравнениями Блоха, описывающими ядерный магнитный резонанс. [7] Ральф Крониг (нидерл. Ralph Kronig; 1904–1995) – нидерландский физик-теоретик, член Нидерландской АН. Работы относятся к спектроскопии, теории молекулярных структур, теории валентности, квантовой механике, ядерной физике, физике твердого тела. [8] Пенни Уильям Джордж (англ. Penney William George, 1909–1991) – английский математик и физик, руководитель британской программы создания атомной бомбы. [9] Де Бройль Луи (фр. Louis-Victor-Pierre-Raymond, 1892–1987) – французский физик-теоретик, один из основателей квантовой механики. За открытие волновой природы электрона получил Нобелевскую премию за 1929 г. Занимался вопросами радиофизики, классической и квантовой теориями поля, термодинамики и других разделов физики. [10] Исаак Ньютон (англ. Sir Isaac Newton, 1643 –1727) – английский физик, математик и астроном, один из создателей классической физики. Автор фундаментального труда «Математические начала натуральной философии», в котором изложил закон всемирного тяготения и три закона механики, ставшие основой классической механики. Разработал дифференциальное и интегральное исчисление, теорию цвета и многие другие математические и физические теории. [11] Брук Тейлор (англ. Brook Taylor, 1685–1731) – английский математик, именем которого называется найденная им известная формула, выражающая приращение функции в виде ряда, расположенного по возрастающим степеням приращения независимой переменной.
[12] Игорь Евгеньевич Тамм (1895– 1971) – советский физик-теоретик, лауреат Нобелевской премии по физике (совместно с П.А. Черенковым и И.М. Франком, 1958). Основные работы в области квантовой механики, физики твёрдого тела, теории излучения, ядерной физики, физики элементарных частиц.
[13] Уильям Бредфорд Шокли (англ. William Bradford Shockley; 1910 – 1989) –американский физик английского происхождения. Работы по физике твердого тела и полупроводников, по теории дислокаций и ферромагнетизма. Шокли построил теорию p-n-перехода и предложил p-n-p-транзистор, разработал метод определения эффективной массы носителей заряда. В 1956 «за исследования полупроводников и открытие транзисторного эффекта» Шокли совместно с Джоном Бардином и Уолтером Браттейном был удостоен Нобелевской премии по физике. [14] Ванье Грегори Хуг ( Wannier Gregory Hugh,1911–1983) – швейцарский физик-теоретик. Работы посвящены теории твердого тела, магнетизму, статистической механике, разрядам в газах, электронной физике. Исследовал молекулярные и кристаллические структуры, локализацию электронов в твердом теле, фазовые переходы. Заложил основы теории экситонов. [15] Невилл Франсис Мотт (сэр) (англ. Sir Nevill Francis Mott; 1905–1996) – английский физик, лауреат Нобелевской премии по физике в 1977 г., совместно с Филипом Андерсоном и Джоном ван Флеком, «за фундаментальные теоретические исследования электронной структуры магнитных и неупорядоченных систем». Дал теоретическое объяснение воздействия света на фотоэмульсию, перехода вещества из металлического в неметаллическое состояние. Его именем названо понятие диэлектрик Мотта. ЭНЕРГЕТИЧЕСКАЯ СТРУКТУРА ТВЕРДЫХ ТЕЛ Дискретные энергетические уровни атомов, образующих твердое тело, под действием возмущающего действия полей окружающих атомов расщепляются в энергетические зоны. Решение уравнения Шредингера в приближении сильной или слабой связи дает качественно одну и ту же картину для структуры энергетических зон твердых тел. Наибольшее значение для электронных свойств твердых тел имеют верхняя и расположенная ниже разрешенные зоны энергий. Если между ними нет энергетического зазора, то твердое тело с такой зонной структурой является металлом. Если величина энергетической щели между этими зонами (запрещенной зоны) больше 3 эВ, то твердое тело является диэлектриком. И, наконец, если ширина запрещенной зоны составляет (0,1 ÷ 3,0) эВ, то твердое тело принадлежит к классу полупроводников. Поскольку в полупроводниках ширина запрещенной зоны меняется в широком диапазоне, то вследствие этого в значительной мере меняется их удельная проводимость. Рассматриваются энергетические состояния в несовершенных кристаллах, вводится понятие энергии Ферми в металлах, уровня Ферми в полупроводниках.
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 694; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.209.151 (0.015 с.) |

 (4.27)
(4.27) (4.28)
(4.28) (4.29)
(4.29) (4.30)
(4.30) – вектор трансляции решетки. В (4.30) второе слагаемое
– вектор трансляции решетки. В (4.30) второе слагаемое  представляет потенциальную энергию электрона в кристалле, третье
представляет потенциальную энергию электрона в кристалле, третье  – энергию взаимодействия атомов.
– энергию взаимодействия атомов. (4.31)
(4.31) Умножая (4.29) на сопряженную волновую функцию
Умножая (4.29) на сопряженную волновую функцию  и интегрируя по всему объему, найдем среднее значение энергии
и интегрируя по всему объему, найдем среднее значение энергии (4.32)
(4.32)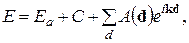 (4.33)
(4.33)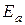 – энергия электрона в изолированном атоме, следующие слагаемые являются поправками первого и второго приближения:
– энергия электрона в изолированном атоме, следующие слагаемые являются поправками первого и второго приближения: (4.34)
(4.34)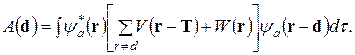 (4.35)
(4.35) один от другого, следовательно, учитывается перекрывание волновых функций по всему кристаллу и электрон тем самым не локализуется возле отдельного атома. Это слагаемое, собственно говоря, отражает влияние поля решетки на движение электрона в кристалле.
один от другого, следовательно, учитывается перекрывание волновых функций по всему кристаллу и электрон тем самым не локализуется возле отдельного атома. Это слагаемое, собственно говоря, отражает влияние поля решетки на движение электрона в кристалле. . Как и в модели Кронига-Пенни, мы пришли к представлению о зонном характере энергетического спектра электрона в кристалле, то есть к существованию разрешенных зон, разделенных запрещенными зонами (рис. 4.1).
. Как и в модели Кронига-Пенни, мы пришли к представлению о зонном характере энергетического спектра электрона в кристалле, то есть к существованию разрешенных зон, разделенных запрещенными зонами (рис. 4.1).

 и
и  для германия,
для германия,  и
и  для кремния.
для кремния. =0,035 эВ.
=0,035 эВ.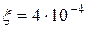 эВ/град:
эВ/град: , (4.54)
, (4.54)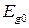 – ширина запрещенной зоны при абсолютном нуле.
– ширина запрещенной зоны при абсолютном нуле. имеют структуру типа цинковой обманки
имеют структуру типа цинковой обманки  . У арсенида галлия
. У арсенида галлия  и антимонида индия
и антимонида индия  абсолютный минимум зоны проводимости лежит при
абсолютный минимум зоны проводимости лежит при 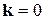 , поэтому у них поверхностями постоянной энергии являются сферы с центром в центре зоны Бриллюэна и эффективные массы электронов равны соответственно
, поэтому у них поверхностями постоянной энергии являются сферы с центром в центре зоны Бриллюэна и эффективные массы электронов равны соответственно  и
и 
 эВ и у антимонида индия –
эВ и у антимонида индия –  эВ.
эВ. эВ выше дна зоны проводимости (нижней долины) (рис.4.12, а).
эВ выше дна зоны проводимости (нижней долины) (рис.4.12, а).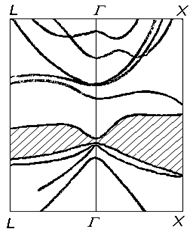

 по сравнению с нижней долиной
по сравнению с нижней долиной  С этой особенностью связана возможность отрицательного дифференциального сопротивления, что позволяет использовать арсенид галлия как материал для диодов Ганна.
С этой особенностью связана возможность отрицательного дифференциального сопротивления, что позволяет использовать арсенид галлия как материал для диодов Ганна. , то есть по два состояния на элементарную ячейку. Поэтому в случае элементов I группы периодической системы (Li, Na, К и др.) энергетическая зона проводимости оказывается заполненной лишь наполовину. В случае двухвалентных элементов (Be, Mg, Ca и др.) их металлические свойства объясняются частичным или полным перекрыванием соседних зон, в результате чего образуется гибридная зона, в которой число состояний больше числа электронов.
, то есть по два состояния на элементарную ячейку. Поэтому в случае элементов I группы периодической системы (Li, Na, К и др.) энергетическая зона проводимости оказывается заполненной лишь наполовину. В случае двухвалентных элементов (Be, Mg, Ca и др.) их металлические свойства объясняются частичным или полным перекрыванием соседних зон, в результате чего образуется гибридная зона, в которой число состояний больше числа электронов. от центра зоны. Поэтому эффективная масса плотности состояний (4.92) с учетом того, что для кремния
от центра зоны. Поэтому эффективная масса плотности состояний (4.92) с учетом того, что для кремния  равна
равна . (4.109)
. (4.109)
 и тяжелые
и тяжелые  дырки. Эффективная масса плотности состояний в валентной зоне кремния равна
дырки. Эффективная масса плотности состояний в валентной зоне кремния равна . (4.110)
. (4.110) . (4.111)
. (4.111)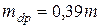 . (4.112)
. (4.112) . (4.133)
. (4.133) (основных носителей) и дырок
(основных носителей) и дырок  (неосновных носителей) в полупроводнике n-типа; дырок
(неосновных носителей) в полупроводнике n-типа; дырок  (основных носителей) и электронов
(основных носителей) и электронов  (неосновных носителей) в полупроводнике р-типа. Тогда соотношение (4.133) можно переписать в следующем виде
(неосновных носителей) в полупроводнике р-типа. Тогда соотношение (4.133) можно переписать в следующем виде . (4.134)
. (4.134) , (4.135)
, (4.135) , (4.136)
, (4.136) (4.137)
(4.137) интеграл Ферми можно аппроксимировать выражением
интеграл Ферми можно аппроксимировать выражением , (4.138)
, (4.138) отвечает случаю полного вырождения полупроводника. Интеграл Ферми при этом может быть аппроксимирован функцией
отвечает случаю полного вырождения полупроводника. Интеграл Ферми при этом может быть аппроксимирован функцией (4.139)
(4.139) , (4.140)
, (4.140) – уровень Ферми при абсолютном нуле.
– уровень Ферми при абсолютном нуле. полупроводник считается слабо вырожденным.
полупроводник считается слабо вырожденным. для натрия и лития (допуская, что
для натрия и лития (допуская, что  ).
). ).
). . Найти:
. Найти:


