
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
формула (4.126) упрощается, и положение уровня Ферми определяется выражениемСодержание книги
Поиск на нашем сайте
Из (4.127) видно, что уровень Ферми при абсолютном нуле температуры проходит посередине между дном зоны проводимости и примесным уровнем. При достаточно низких температурах (пока
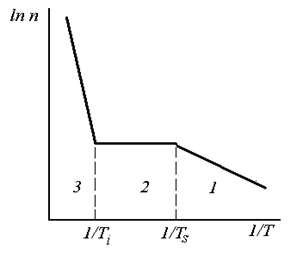
Эта область называется областью слабой ионизации примеси (на рис.4.21 она отмечена цифрой 1). При последующем повышении температуры концентрация электронов в зоне проводимости растет, а концентрация электронов на примесных уровнях уменьшается. При выполнении неравенства
формула (4.126) аппроксимируется выражением
которому соответствует
Это означает, что практически вся донорная примесь оказывается ионизированной, и концентрация электронов в зоне проводимости не зависит от температуры. Эта область температур называется областью истощения примеси (или областью насыщения) и на рис. 4.21 обозначена цифрой 2. Температура
При последующем повышении температуры увеличение концентрации электронов в зоне проводимости будет происходить за счет переходов электронов из валентной зоны. В этом случае положения уровня Ферми и концентрация электронов определяются уравнениями (4.120), (4.130) и (4.121). На рис.4.21 область 3 отвечает области собственной проводимости. В этом случае
Таким образом, используя описанные приближения, можно проследить изменение концентрации электронов (рис.4.22) и положения уровня Ферми (рис.4.21, а) для невырожденного электронного полупроводника во всей области изменения температур. Акцепторный полупроводник. Аналогичные расчеты можно провести для полупроводника, легированного акцепторной примесью. В дырочном полупроводнике при температуре абсолютного нуля уровень Ферми лежит посередине между потолком валентной зоны и уровнем акцепторной примеси. С повышением температуры уровень Ферми будет стремиться к середине запрещенной зоны. Положение уровня Ферми в зависимости от температуры для дырочного полупроводника изображено на рис.4.21, б.
Закон действующих масс
В примесном полупроводнике имеются основные и неосновные носители заряда. Для полупроводника n-типа (электронного) основными являются электроны, а дырки – неосновными. Для полупроводника р-типа ( дырочного) основными являются дырки, электроны – неосновными. В полупроводнике равновесная концентрация электронов в зоне проводимости определяется выражением (4.115), а дырок в валентной зоне – (4.116). Перемножив эти выражения, получим
Обозначим концентрации: электронов
Соотношение (4.134) называется законом действующих масс: для данной температуры произведение равновесных концентраций основных и неосновных носителей заряда есть величина постоянная и равная квадрату концентрации собственных носителей. Выражение (4.134) обычно используют для определения концентрации неосновных носителей заряда. Вырожденные полупроводники. Степень вырожденности полупроводника определяется положением уровня Ферми. Для ее оценки удобно пользоваться величиной приведенного уровня Ферми. Концентрацию электронов в зоне проводимости, используя (4.76) и безразмерные параметры
можно представить в виде
где
называется интегралом Ферми. Величина h называется приведенным уровнем Ферми. При
что соответствует статистике Больцмана, и, следовательно, полупроводник является невырожденным. Условие
и равновесная концентрация электронов в вырожденном донорном полупроводнике определяется из (4.136)
где При условии
Контрольные вопросы и задачи
1. В чем суть адиабатического и одноэлектронного приближения при решении уравнения Шредингера для электронов в кристалле? 2. Что такое идеальная кристаллическая решетка и как она влияет на движение электрона в кристалле? 3. В чем сущность модели Кронига-Пенни? 4. Что такое зона Бриллюэна? 5. Чем определяется число уровней в энергетической зоне? 6. Эффективная масса электрона в кристалле и ее физическая суть. 7. Что такое дырка с точки зрения зонной теории? 8. Понятие полупроводника, металла и диэлектрика в зонной теории. 9. Что такое водородоподобная модель примесного состояния? 10. Как возникают уровни Тамма? 11. Что собой представляют экситоны? 12. Что такое энергия Ферми и как она зависит от концентрации электронов в металле? 13. Рассчитайте энергию Ферми при 14. Определить температуру Ферми и фермиевскую скорость электронов для меди, которая является одновалентным металлом (предполагая, что 15. В полупроводнике ZnSb ширина запрещенной зоны – энергию ионизации доноров; – радиус орбиты электрона в основном состоянии; – при какой минимальной концентрации доноров станут заметны эффекты, связанные с перекрытием орбит соседних примесных атомов?
Литература к главе
1. Фридрихов, С.Ф. Физические основы электронной техники [Текст]: учеб. / С.Ф. Фридрихов, С.М. Мовнин. – М.: Высш. школа, 1982. – 608 с. 2. Епифанов, Г.И. Физика твердого тела [Текст]: учеб. пособие / Г.И.Епифанов. – М.: Высш. школа, 1977. – 288 с. 3. Шалимова, К.В. Физика полупроводников [Текст]: учеб. пособие / К.В.Шалимова. – М.: Энергия, 1971. – 312 с. 4. Черняков, Е.І. Фізика твердого тіла [Текст]: навч. посібник/ Е.І. Черняков, О.С.Замковий, Г.Г.Канарик. – Харків: Колегіум, 2006. – 264 с.
[1] Георг Симон Ом (нем. Georg Simon Ohm; 1787 – 1854) – знаменитый немецкий физик. Установил основной закон электрической цепи (закон Ома). Труды по акустике, кристаллооптике. [2] Джеймс Прескотт Джоуль (англ. James Prescott Joule; 1818- 1889) – английский физик. Джоуль изучал природу тепла и обнаружил её связь с механической работой, открыл связь между током, текущим через проводник с определённым сопротивлением, и выделяющимся при этом теплом (закон Джоуля). [3] Эмилий Христианович Ленц (нем. Heinrich Friedrich Emil Lenz; 1804 – 1865) – знаменитый русский физик. Главнейшие результаты его исследований: закон индукции (правило Ленца), закон Джоуля-Ленца, опыты, подтверждающие явление Пельтье. [4]Матиссен Огастес (1831–1870) – английский физик. [5] Уильям Роуэн Гамильтон (англ. William Rowan Hamilton; 1805 –1865) – выдающийся ирландский математик и физик XIX века. Оба главных открытия Гамильтона – новая формулировка механики и кватернионы –сыграли существенную роль в XX веке при возникновении квантовой механики. [6] Феликс Блох (нем. Felix Bloch; 1905 –1983) – швейцарский физик, работавший главным образом в США. Лауреат Нобелевской премии по физике за 1952 год (совместно с Эдвардом Пёрселлом). Работы посвящены физике твердого тела, магнетизму, квантовой электродинамике, сверхпроводимости, ядерной физике. Заложил (совместно с Л. Бриллюэном) основы зонной теории твердых тел (1928) и низкотемпературного ферромагнетизма. Известен также формулой Бете – Блоха для тормозной способности, теоремой Блоха в теории сверхпроводимости, теоремой Блоха–Нордсека в квантовой электродинамике, уравнениями Блоха, описывающими ядерный магнитный резонанс. [7] Ральф Крониг (нидерл. Ralph Kronig; 1904–1995) – нидерландский физик-теоретик, член Нидерландской АН. Работы относятся к спектроскопии, теории молекулярных структур, теории валентности, квантовой механике, ядерной физике, физике твердого тела. [8] Пенни Уильям Джордж (англ. Penney William George, 1909–1991) – английский математик и физик, руководитель британской программы создания атомной бомбы. [9] Де Бройль Луи (фр. Louis-Victor-Pierre-Raymond, 1892–1987) – французский физик-теоретик, один из основателей квантовой механики. За открытие волновой природы электрона получил Нобелевскую премию за 1929 г. Занимался вопросами радиофизики, классической и квантовой теориями поля, термодинамики и других разделов физики. [10] Исаак Ньютон (англ. Sir Isaac Newton, 1643 –1727) – английский физик, математик и астроном, один из создателей классической физики. Автор фундаментального труда «Математические начала натуральной философии», в котором изложил закон всемирного тяготения и три закона механики, ставшие основой классической механики. Разработал дифференциальное и интегральное исчисление, теорию цвета и многие другие математические и физические теории. [11] Брук Тейлор (англ. Brook Taylor, 1685–1731) – английский математик, именем которого называется найденная им известная формула, выражающая приращение функции в виде ряда, расположенного по возрастающим степеням приращения независимой переменной.
[12] Игорь Евгеньевич Тамм (1895– 1971) – советский физик-теоретик, лауреат Нобелевской премии по физике (совместно с П.А. Черенковым и И.М. Франком, 1958). Основные работы в области квантовой механики, физики твёрдого тела, теории излучения, ядерной физики, физики элементарных частиц.
[13] Уильям Бредфорд Шокли (англ. William Bradford Shockley; 1910 – 1989) –американский физик английского происхождения. Работы по физике твердого тела и полупроводников, по теории дислокаций и ферромагнетизма. Шокли построил теорию p-n-перехода и предложил p-n-p-транзистор, разработал метод определения эффективной массы носителей заряда. В 1956 «за исследования полупроводников и открытие транзисторного эффекта» Шокли совместно с Джоном Бардином и Уолтером Браттейном был удостоен Нобелевской премии по физике. [14] Ванье Грегори Хуг ( Wannier Gregory Hugh,1911–1983) – швейцарский физик-теоретик. Работы посвящены теории твердого тела, магнетизму, статистической механике, разрядам в газах, электронной физике. Исследовал молекулярные и кристаллические структуры, локализацию электронов в твердом теле, фазовые переходы. Заложил основы теории экситонов. [15] Невилл Франсис Мотт (сэр) (англ. Sir Nevill Francis Mott; 1905–1996) – английский физик, лауреат Нобелевской премии по физике в 1977 г., совместно с Филипом Андерсоном и Джоном ван Флеком, «за фундаментальные теоретические исследования электронной структуры магнитных и неупорядоченных систем». Дал теоретическое объяснение воздействия света на фотоэмульсию, перехода вещества из металлического в неметаллическое состояние. Его именем названо понятие диэлектрик Мотта.
|
||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 441; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.009 с.) |

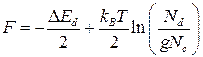 . (4.127)
. (4.127) ) уровень Ферми повышается до некоторого максимального, а затем начинает снижаться. Такому изменению уровня Ферми отвечает экспоненциальная зависимость концентрации электронов от температуры
) уровень Ферми повышается до некоторого максимального, а затем начинает снижаться. Такому изменению уровня Ферми отвечает экспоненциальная зависимость концентрации электронов от температуры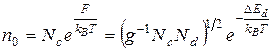 . (4.128)
. (4.128)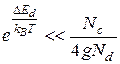
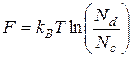 , (4.129)
, (4.129) . (4.130)
. (4.130) , при которой
, при которой 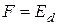 , называется температурой насыщения, и ее можно определить из условия
, называется температурой насыщения, и ее можно определить из условия . (4.131)
. (4.131)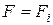 ; воспользовавшись (4.120), (4.130), получаем уравнение для определения температуры перехода к собственной проводимости
; воспользовавшись (4.120), (4.130), получаем уравнение для определения температуры перехода к собственной проводимости . (4.132)
. (4.132)
 . (4.133)
. (4.133) (основных носителей) и дырок
(основных носителей) и дырок  (неосновных носителей) в полупроводнике n-типа; дырок
(неосновных носителей) в полупроводнике n-типа; дырок  (основных носителей) и электронов
(основных носителей) и электронов  (неосновных носителей) в полупроводнике р-типа. Тогда соотношение (4.133) можно переписать в следующем виде
(неосновных носителей) в полупроводнике р-типа. Тогда соотношение (4.133) можно переписать в следующем виде . (4.134)
. (4.134) , (4.135)
, (4.135) , (4.136)
, (4.136) (4.137)
(4.137) интеграл Ферми можно аппроксимировать выражением
интеграл Ферми можно аппроксимировать выражением , (4.138)
, (4.138) отвечает случаю полного вырождения полупроводника. Интеграл Ферми при этом может быть аппроксимирован функцией
отвечает случаю полного вырождения полупроводника. Интеграл Ферми при этом может быть аппроксимирован функцией (4.139)
(4.139) , (4.140)
, (4.140) – уровень Ферми при абсолютном нуле.
– уровень Ферми при абсолютном нуле. полупроводник считается слабо вырожденным.
полупроводник считается слабо вырожденным. для натрия и лития (допуская, что
для натрия и лития (допуская, что  ).
). ).
). . Найти:
. Найти:


