Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика плоского движения твердого телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Положение тела определяется положением полюса и углом поворота тела вокруг полюса. Дифф-ные уравнения плоского движения тв. тела:
Силой трения называют силу, которая возникает при движении одного тела по поверхности другого. Она всегда направлена противоположно направлению движения. Сила трения прямо пропорциональна силе нормального давления на трущиеся поверхности и зависит от свойств этих поверхностей. Законы трения связаны с электромагнитным взаимодействием, которое существует между телами. Различают трение внешнее и внутреннее. Внешнее трение возникает при относительном перемещении двух соприкасающихся твердых тел (трение скольжения или трение покоя). Внутреннее трение наблюдается при относительном перемещении частей одного и того же сплошного тела (например, жидкость или газ). Различают сухое и жидкое (или вязкое) трение. Сухое трение возникает между поверхностями твердых тел в отсутствие смазки. Жидким (вязким) называется трение между твердым телом и жидкой или газообразной средой или ее слоями. Сухое трение, в свою очередь, подразделяется на трение скольжения и трение качения. Рассмотрим законы сухого трения (рис. 4.5).
Подействуем на тело, лежащее на неподвижной плоскости, внешней силой Установлено, что максимальная сила трения покоя не зависит от площади соприкосновения тел и приблизительно пропорциональна модулю силы нормального давления N:
μ0 – коэффициент трения покоя, зависящий от природы и состояния трущихся поверхностей. Когда модуль внешней силы, а следовательно, и модуль силы трения покоя превысит значение F 0, тело начнет скользить по опоре – трение покоя F тр.пок сменится трением скольжения F ск (рис. 4.6):
где μ – коэффициент трения скольжения. Трение качения возникает между шарообразным телом и поверхностью, по которой оно катится. Сила трения качения подчиняется тем же законам, что и сила трения скольжения, но коэффициент трения μ; здесь значительно меньше. Подробнее рассмотрим силу трения скольжения на наклонной плоскости (рис. 4.7). На тело, находящееся на наклонной плоскости с сухим трением, действуют три силы: сила тяжести
Если F тр = μ N = mg cosα, При α > αmax тело будет скатываться с ускорением a = g (sinα - μ cosα), Деформа́ция (от лат. deformatio — «искажение») — изменение взаимного положения частиц тела, связанное с их перемещением относительно друг друга. Деформация представляет собой результат изменения межатомных расстояний и перегруппировки блоков атомов. Обычно деформация сопровождается изменением величин межатомных сил, мерой которого является упругое механическое напряжение. По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом: · Деформация растяжения; · Деформация сжатия; · Деформация сдвига (или среза); · Деформация при кручении; · Деформация при изгибе. Если принять направление внешней силы, стремящейся удлинить образец, за положительное, то F > 0 при деформации растяжения и F < 0 – при сжатии. Отношение модуля внешней силы F к площади S сечения тела называется механическим напряжением σ:
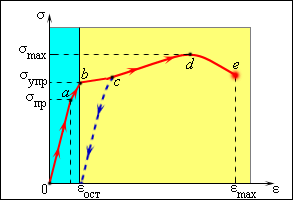
Зависимость между ε и σ является одной из важнейших характеристик механических свойств твердых тел. Графическое изображение этой зависимости называется диаграммой растяжения. По оси абсцисс откладывается относительное удлинение ε, а по оси ординат – механическое напряжение σ. Типичный пример диаграммы растяжения для металлов (таких как медь или мягкое железо) представлен на рис. 3.7.2.
При малых деформациях (обычно существенно меньших 1 %) связь между σ и ε оказывается линейной (участок Oa на диаграмме). При этом при снятии напряжения деформация исчезает. Такая деформация называется упругой. Максимальное значениеσ = σпр, при котором сохраняется линейная связь между σ и ε, называется пределом пропорциональности (точка a). На линейном участке выполняется закон Гука:
Если σ > σупр, образец после снятия напряжения уже не восстанавливает свои первоначальные размеры и у тела сохраняется остаточная деформация εост. Такие деформации называются пластическими (участки bc, cd и de). На участке bc деформация происходит почти без увеличения напряжения. Это явление называется текучестью материала. В точке d достигается наибольшее напряжение σmax, которое способен выдержать материал без разрушения (предел прочности). В точке e происходит разрушение материала. Преде́л про́чности — механическое напряжение
Стационарное течение жидкости - это такое течение, при котором скорость жидкости в каждой данной точке остается постоянной как по величине, так и по направлению. Для стационарного течения форма и расположение линий тока со временем не изменяются. Рассмотрим какую-либо трубку тока. За время dt через произвольное сечение S ходит объем жидкости Svdt. Выберем два ее сечения. Гидродинамика занимается изучением движения несжимаемых жидкостей и их взаимодействия с твердыми телами. Для описания движения несжимаемых жидкостей, вводят понятие линий тока. Линии, касательные к которым в каждой точке совпадают с вектором скорости v, называются линиями тока. Густота линий пропорциональна величине скорости в данном месте. В общем случае величина и направление вектора v может меняться с течением времени. Если же вектор скорости в каждой точке жидкости остается постоянным, то течение называется установившимся, или стационарным. Картина линий тока при стационарном течении остается неизменной, и линии тока в этом случае совпадают с траекториями частиц жидкости. Часть жидкости, ограниченная линиями тока называется трубкой тока. Ясно, что жидкость не может вытекать или втекать через боковую поверхность трубки тока. Так как жидкость несжимаема, то количество жидкости, протекающее через любое поперечное сечение одной и той же трубки тока одинаково. Следовательно, можно записать: S•v=const (1.66) где S - поперечное сечение трубки тока, v - скорость жидкости для этой трубки тока. Данное уравнение называют уравнением неразрывности струи.
Уравнение Бернулли для жидкости
Уравнение Бeрнýлли для жидкостив самом простейшем виде записывается так:
. Полная энергия жидкости складывается из ее Потенциальной энергии в поле сил тяжести и поверхностной энергии, обусловленной силами поверхностного натяжения.
Все течения жидкости и газа качественно разделяются на 2 режима – ламинарный и турбулентный. Ламинарное течение (lamina – пластинка, полоска) – это упорядоченное плавное течение жидкости, при котором жидкость перемещается как бы слоями, параллельными направлению течения (например – стенкам цилиндрической трубы), не перемешиваясь. Эти течения наблюдаются или у очень вязких жидкостей, или при малых скоростях течения, а также при течениях в узких трубках или при обтекании тел малых размеров. Вообще тот или иной режим течения характеризуется числом Рейнольдса Для каждого вида течения существует такое критическое число Рейнольдса, что при Re<Reкр возможно только ламинарное течение, в то время как при Re>Reкр течение может потерять устойчивость по отношению к малым возмущениям (случайным отклонениям) исходных параметров и стать турбулентным (например, для течения жидкости в цилиндрической трубе круглого поперечного сечения диаметром d Re = V ср d /Ѕ – Reкр H 2300). При турбулентном течении (turbulentus – беспорядочный, вихревой) частицы жидкости совершают неустановившиеся движения по сложным траекториям, что приводит к интенсивному перемешиванию между слоями жидкости, т.е. слоистая структура течения нарушается; при этом местные значения параметров движения – V, p, T,… испытывают хаотические флуктуации, т.е. случайные отклонения от средних значений, и изменяются нерегулярно во времени и пространств Точное описание турбулентных течений весьма сложно, поэтому обычно для упрощения их условно заменяют фиктивными слоистыми течениями с некоторыми осредненными по времени скоростями число, или, правильнее, критерий Рейно́льдса ( Число Рейнольдса определяется следующим соотношением: Re = vLρ/η где ρ — плотность жидкости, v — скорость потока, а L — характерная длина элемента потока (в этой формуле важно помнить, что Re — это одно число, а не произведение R × e). Теперь давайте посмотрим на размерность составляющих числа Рейнольдса: · размерность коэффициента вязкости η — ньютоны умножить на секунды разделить на кв. метры, или н · с / м 2. Если вспомнить, что, по определению, н = кг · м / c 2, мы получим кг / м · с · размерность плотности ρ — килограммы разделить на кубические метры, или кг / м 3 · размерность скорости v — метры разделить на секунды, или м / с · размерность длины элемента потока L — метры, или м Наиболее обтекаемо такое тело, которое при данной лобовой площади имеет наименьшее сопротивление. Форма тела, закруглённого спереди и заострённого сзади, возможно более гладкая, без выступов, является наиболее обтекаемой. Такую форму придают снарядам, подводным лодкам, торпедам, гоночным автомобилям, корпусу и крыльям самолёта, подводным частям судов.? Выясним теперь, какими физическими процессами определяется уменьшение сопротивления движению тела, которому придана обтекаемая форма. Для этого будем помещать в поток жидкости тела различной формы и, меняя скорость потока, наблюдать картины линий тока, получившиеся при обтекании жидкостью этих тел. На рисунке изображена картина линий тока жидкости, получившаяся при обтекании ею цилиндра с различной скоростью. При малых скоростях обтекания линии тока, обойдя цилиндр, располагаются позади него так же, как и перед ним. По мере же увеличения скорости обтекания жидкость позади цилиндра приходит в круговое вихревое движение. Жидкость, вращающаяся в вихре, движется быстрее жидкости в стационарном потоке. Но мы знаем, что давление в жидкости тем меньше, чем быстрее она движется (вспомните всасывающее действие струи жидкости). Следовательно, с задней стороны цилиндра, где образовались вихри, давление становится меньше, чем с передней. Разность давлений впереди и позади движущегося тела и создаёт сопротивление движению тела. К этому сопротивлению присоединяется ещё сопротивление, обусловленное внутренним трением; оно выражается в том, что движущееся тело увлекает за собой слои жидкости. Однако измерения показывают, что это сопротивление мало, и при больших скоростях существенного значения оно не имеет. Итак, главнейшей причиной, обусловливающей сопротивление жидкости движению тела, является образование вихрей позади движущегося тела, обусловленное также вязкостью жидкости. Поэтому для уменьшения этого сопротивления надо придать телу такую форму, при которой завихрение жидкости получается наименьшим. Тело обтекаемой формы обладает малым сопротивлением потому, что жидкость всюду прилегает к его поверхности и позади него не завихрена. На рисунке изображена картина линий тока вокруг тела обтекаемой формы. Сзади такого тела вихри почти не образуются. Лобовое сопротивление — сила, препятствующая движению тел в жидкостях и газах. Лобовое сопротивление складывается из двух типов сил: сил касательного (тангенциального) трения, направленных вдоль поверхности тела, исил давления, направленных по нормали к поверхности. Сила сопротивления является диссипативной силой и всегда направлена против вектора скорости тела в среде. Наряду с подъёмной силой является составляющей полной аэродинамической силы. Сила лобового сопротивления обычно представляется в виде суммы двух составляющих: сопротивления при нулевой подъёмной силе и индуктивного сопротивления. Каждая составляющая характеризуется своим собственным безразмерным коэффициентом сопротивления и определённой зависимостью от скорости движения. Подъёмная сила — составляющая полной аэродинамической силы, перпендикулярная вектору скорости движения тела в потоке жидкости или газа, возникающая в результате несимметричности обтекания тела потоком. В соответствии с законом Бернулли, статическое давление среды в тех областях, где скорость потока более высока, будет ниже, и наоборот. Например, крыло самолета имеет несимметричный профиль (верхняя часть крыла более выпуклая), вследствие чего скорость потока по верхней кромке крыла будет выше, чем над нижней. Создавшаяся разница давлений и порождает подъёмную силу.
Эффект Магнуса — физическое явление, возникающее при обтекании вращающегося тела потоком жидкости или газа. Образуется сила, воздействующая на тело и направленная перпендикулярно направлению потока. Это является результатом совместного воздействия различных физических явлений, таких как эффект Бернулли и образование пограничного слоя в среде вокруг обтекаемого объекта. Вращающийся объект создаёт в среде вокруг себя вихревое движение. С одной стороны объекта направление вихря совпадает с направлением обтекающего потока и, соответственно, скорость движения среды с этой стороны увеличивается. С другой стороны объекта направление вихря противоположно направлению движения потока, и скорость движения среды уменьшается. Ввиду этой разности скоростей возникает разность давлений, порождающая поперечную силу от той стороны вращающегося тела, на которой направление вращения и направление потока противоположны, к той стороне, на которой эти направления совпадают
Ламинарное течение (lamina – пластинка, полоска) – это упорядоченное плавное течение жидкости, при котором жидкость перемещается как бы слоями, параллельными направлению течения (например – стенкам цилиндрической трубы), не перемешиваясь. Эти течения наблюдаются или у очень вязких жидкостей, или при малых скоростях течения, а также при течениях в узких трубках или при обтекании тел малых размеров. Вообще тот или иной режим течения характеризуется числом Рейнольдса Для каждого вида течения существует такое критическое число Рейнольдса, что при Re<Reкр возможно только ламинарное течение, в то время как при Re>Reкр течение может потерять устойчивость по отношению к малым возмущениям (случайным отклонениям) исходных параметров и стать турбулентным (например, для течения жидкости в цилиндрической трубе круглого поперечного сечения диаметром d Re = Vсрd/Ѕ – Reкр H 2300).
Схематичное изображение ламинарного (a) и турбулентного (b) течения в плоском слое Ламина́рное тече́ние (лат. lāmina — «пластинка») — течение, при котором жидкость или газ перемещается слоями без перемешивания и пульсаций (то есть беспорядочных быстрых изменений скорости и давления).
Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда действующие силы неизвестны. Примером такого рода задач является ударное взаимодействие тел. С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц). Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин. В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары. Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело. При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание). Примером абсолютно неупругого удара может служить попадание пули (или снаряда) в баллистический маятник. Маятник представляет собой ящик с песком массой M, подвешенный на веревках (рис. 1.21.1). Пуля массой m, летящая горизонтально со скоростью Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел. Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара. При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии. Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя (рис. 1.21.2). Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров. коэффициент восстановления относительной скорости - в теории удара, величина, зависящая от упругих свойств соударяющихся тел и определяющая, какая доля начальной относительной скорости этих тел восстанавливается к концу удара (см. Удар). В. к. характеризует потери механической энергии соударяющихся тел вследствие появления в них остаточных деформаций и их нагревания. При прямом ударе тела о неподвижную преграду (плиту) В. к. k = u/v, где v и u — скорости тела в начале и в конце удара по отношению к плите.
Молекулярно-кинетическая теория (МКТ) – это учение, которое объясняет тепловые явления в макроскопических телах и внутренние свойства этих тел движением и взаимодействием атомов, молекул и ионов, из которых состоят тела. В основе МКТ строения вещества лежат три положения: 1. Вещество состоит из частиц – молекул, атомов и ионов. В состав этих частиц входят более мелкие элементарные частицы. Молекула – наименьшая устойчивая частица данного вещества. Молекула обладает основными химическими свойствами вещества. Молекула является пределом деления вещества, то есть самой маленькой частью вещества, которая способна сохранять свойства этого вещества. Атом – это наименьшая частица данного химического элемента. 2. Частицы, из которых состоит вещество, находятся в непрерывном хаотическом (беспорядочном) движении. 3. Частицы вещества взаимодействуют друг с другом – притягиваются и отталкиваются.
Существуют два определения понятия идеального газа: термодинамическое и молекулярно-кинетическое. В термодинамике под идеальным газом понимают газ, у которого при изотермическом процессе при постоянной массе давление обратно пропорционально его объему (или газ, в точности подчиняющийся газовым законам). Модель «идеальный газ» имеет определенные границы применимости: она не применима при высоких давлениях и низких температурах. Если газ сжать, то увеличится его плотность и уменьшатся расстояния между молекулами, поэтому размерами молекул уже нельзя пренебречь, а давление газа будет зависеть не только от ударов молекул, но и от их взаимодействия. Из эксперимента известно, что при давлении газа ~ 108 Па наблюдают существенные отклонения от закона Бойля — Мариотта. То же самое происходит и при понижении температуры. Для измерения масс атомов и молекул в физике и химии принята единая система измерения. Эти величины измеряются в относительных единицах – атомных единицах массы. Атомная единица массы (а.е.м.) равна 1/12 массы m атома углерода 12С (m одного атома 12С равна 1,993 • 10-26 кг). Относительная атомная масса элемента (Ar) – это безразмерная величина, равная отношению средней массы атома элемента к 1/12 массы атома 12С. При расчете относительной атомной массы учитывается изотопный состав элемента. Величины Ar определяют по таблице Д.И. Менделеева. Абсолютная масса атома (m) равна относительной атомной массе, умноженной на 1 а.е.м. Например, для атома водорода абсолютная масса определяется следующим образом: m (H) = 1,008 • 1,661 • 10-27 кг = 1,674 • 10-27 кг Относительная молекулярная масса соединения (Mr) – это безразмерная величина, равная отношению массы m молекулы вещества к 1/12 массы атома 12С: Относительная молекулярная масса равна сумме относительных масс атомов, входящих в состав молекулы. Например: М r (C2H6) = 2 • A r (C) + 6 • A r (H) = 2 • 12 + 6 = 30. Абсолютная масса молекулы равна относительной молекулярной массе, умноженной на 1 а.е.м. m (C2H6) = Mr (C2H6) • 1,661 • 10-27 кг = 49,82 • 10-27 кг. Количество вещества — физическая величина, характеризующая количество однотипных структурных единиц, содержащихся в веществе. Под структурными единицами понимаются любые частицы, из которых состоит вещество (атомы,молекулы, ионы, электроны или любые другие частицы). Единица измерения количества вещества в СИ — моль. n = V/Vm; Vm = 22,4 л/моль (постоянная) АВОГАДРО ЧИСЛО, N A = (6,0220450,000031)1023, число молекул в моле любого вещества или число атомов в моле простого вещества. Одна из фундаментальных постоянных, с помощью которой можно определить такие величины, как, например, массу атома или молекулы (см. ниже), заряд электрона и т.д. Опытное определение постоянной Авогадро. Воспользовавшись идеей распределения молекул по высоте, французский ученый Ж. Перрен (1870—1942) экспериментально нашел значение постоянной Авогадро. Во время исследований под микроскопом броуновского движения, он увидел, что броуновские частицы распределяются по высоте подобно молекулам газа в поле тяготения. Применив к ним больцмановское распределение, можно записать <L1>\<L2>=n1\n2=p1\p2 где m—масса частицы, m1—масса вытесненной ею жидкости; m=4/3πr3ρ, m1=4/3πr3ρ1 (r — радиус частицы, ρ — плотность частицы, ρ1 — плотность жидкости).
Молекулярно-кинетическая теория (сокращённо МКТ) — теория XIX века, рассматривавшая строение вещества, в основном газов, с точки зрения трёх основных приближенно верных положений: Броуновское движение - беспорядочное движение взвешенных в жидкости частиц за счет соударения с молекулами жидкости Диффузия - явление проникновения молекул одного вещества в промежутки между молекулами другого
Давление газа на стенку сосуда есть результат ударов мапе-кул газа об эту стенку. При каждом ударе молекула газа действует на стенку с определенной (с макроскопической точки зрения бесконечно малой) силой. Обратно направленная сила, с которой действует на молекулу стенка сосуда, заставляет молекулу отражаться от стенки. Если бы в сосуде содержалось всего несколько молекул, го пх удары следовали бы друг за другом редко и беспорядочно, п нельзя было бы говорить ни о какой регулярной силе давления, действующей на стенку. Мы имели бы дело с отдельными практически мгновенными бесконечно малыми толчками, которым время от времени подвергалась бы стенка. Если же число молекул в сосуде очень велико, то будет велико и числе ударов их о стенку сосуда. Удары станут следовать непрерывно друг за другом. Одновременно о стенку сосуда будет ударяться громадное количество молекул. Бесконечно малые силы отдельных ударов складываются в конечную и почти постоянную силу, действующую на стенку. Эта сила, усредненная по времени, и есть давление газа, с которым имеет дело макроскопическая физика.
- основное уравнение МКТ идеального газа. Выведено в предположении, что давление газа есть результат ударов его молекул о стенки сосуда. Это же уравнение в другой записи:
Давление смеси химически не взаимодействующих идеальных газов равно сумме парциальных давлений.
Температу́ра (от лат. temperatura — надлежащее смешение, нормальное состояние) — скалярная физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. Температура всех частей системы, находящейся в равновесии, одинакова. Если система не находится в равновесии, то между её частями, имеющими различную температуру, происходит теплопередача (переход энергии от более нагретых частей системы к менее нагретым), приводящая к выравниванию температур в системе. Из того, что температура — это кинетическая энергия молекул, ясно, что наиболее естественно измерять её в энергетических единицах (то есть в системе СИ в джоулях). Однако измерение температуры началось задолго до создания молекулярно-кинетической теории, поэтому практические шкалы измеряют температуру в условных единицах — градусах. Ке́львин (обозначение: K) — единица термодинамической температуры в Международной системе единиц (СИ), одна из семи основных единиц СИ. Предложена в 1848 году. Один кельвин равен 1/273,16 части термодинамической температуры тройной точки воды[1]. Начало шкалы (0 К) совпадает с абсолютным нулём. Пересчёт в градусы Цельсия: °С = K−273,15 (температура тройной точки воды — 0,01 °C). Термо́метр (греч. θέρμη — тепло; μετρέω — измеряю) —прибор для измерения температуры воздуха, почвы, воды и так далее. Существует несколько видов термометров: · жидкостные · механические · электрические · оптические · газовые · инфракрасные
Закон Бойля-Мариотта - Для данной массы газа m при неизменной температуре Т произведение давления на объем есть величина постоянная:
Гей-Люссаком - Для данной массы m при постоянном давлении р объем газа линейно зависит от температуры:
Шарлем - Для данной массы m при постоянном объеме V давление газа линейно зависит от температуры:
Опытные законы Бойля-Мариотта, Гей-Люссака и Шарля справедливы для широкого интервала давлений, объемов и температур. Однако когда давления превышают атмосферное в 300-400 раз, или температуры очень высоки, наблюдаются отклонения от этих законов. Тем не менее, во многих случаях эти законы удобны для практического применения. Если бы существовал газ, для которого не было бы отклонений от этих законов, то такой газ был бы идеальным газом.
40 Состояние идеального газа. Частицы (атомы, молекулы) реально существующих газов обладают собственными размерами, занимают некоторый объем пространства, и в некоторой степени зависимы друг от друга. Силы физического взаимодействия между частицами газа затрудняют их движение и уменьшают их подвижность. По этим причинам газовые законы и следствия из них достаточно строго соблюдаются только для разреженных реальных газов, для которых рассояние между частицами значительно превышает собственный размер частиц газа, а взаимодействие между частицами сведено к минимуму. При обычном (атмосферном) давлении газовые законы становятся прибл
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 1306; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.205.110 (0.012 с.) |

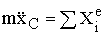 ;
; 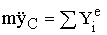 ;
; 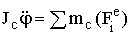 , С – центр масс тела, JC – момент инерции тела относительно оси, перпендикулярной плоскости движения тела и проходящей через его центр масс.
, С – центр масс тела, JC – момент инерции тела относительно оси, перпендикулярной плоскости движения тела и проходящей через его центр масс. Рис. 4.5
Рис. 4.5
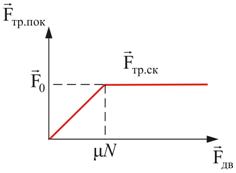 Рис. 4.6
Рис. 4.6
 , постепенно увеличивая ее модуль. Вначале брусок будет оставаться неподвижным, значит, внешняя сила
, постепенно увеличивая ее модуль. Вначале брусок будет оставаться неподвижным, значит, внешняя сила 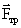 , направленной по касательной к трущейся поверхности, противоположной силе
, направленной по касательной к трущейся поверхности, противоположной силе 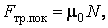
 , нормальная сила реакции опоры
, нормальная сила реакции опоры 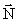 и сила сухого трения
и сила сухого трения 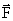 есть равнодействующая сил
есть равнодействующая сил 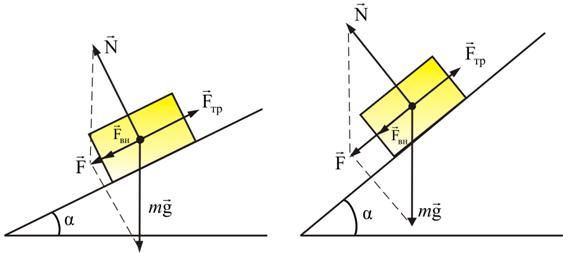 Рис. 4.7
Рис. 4.7
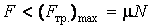 – тело остается неподвижным на наклонной плоскости. Максимальный угол наклона α определяется из условия (F тр)max = F или μ mg cosα = mg sinα, следовательно, tg αmax = μ, где μ – коэффициент сухого трения.
– тело остается неподвижным на наклонной плоскости. Максимальный угол наклона α определяется из условия (F тр)max = F или μ mg cosα = mg sinα, следовательно, tg αmax = μ, где μ – коэффициент сухого трения.
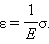
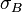 , выше которого происходит разрушение материала.
, выше которого происходит разрушение материала.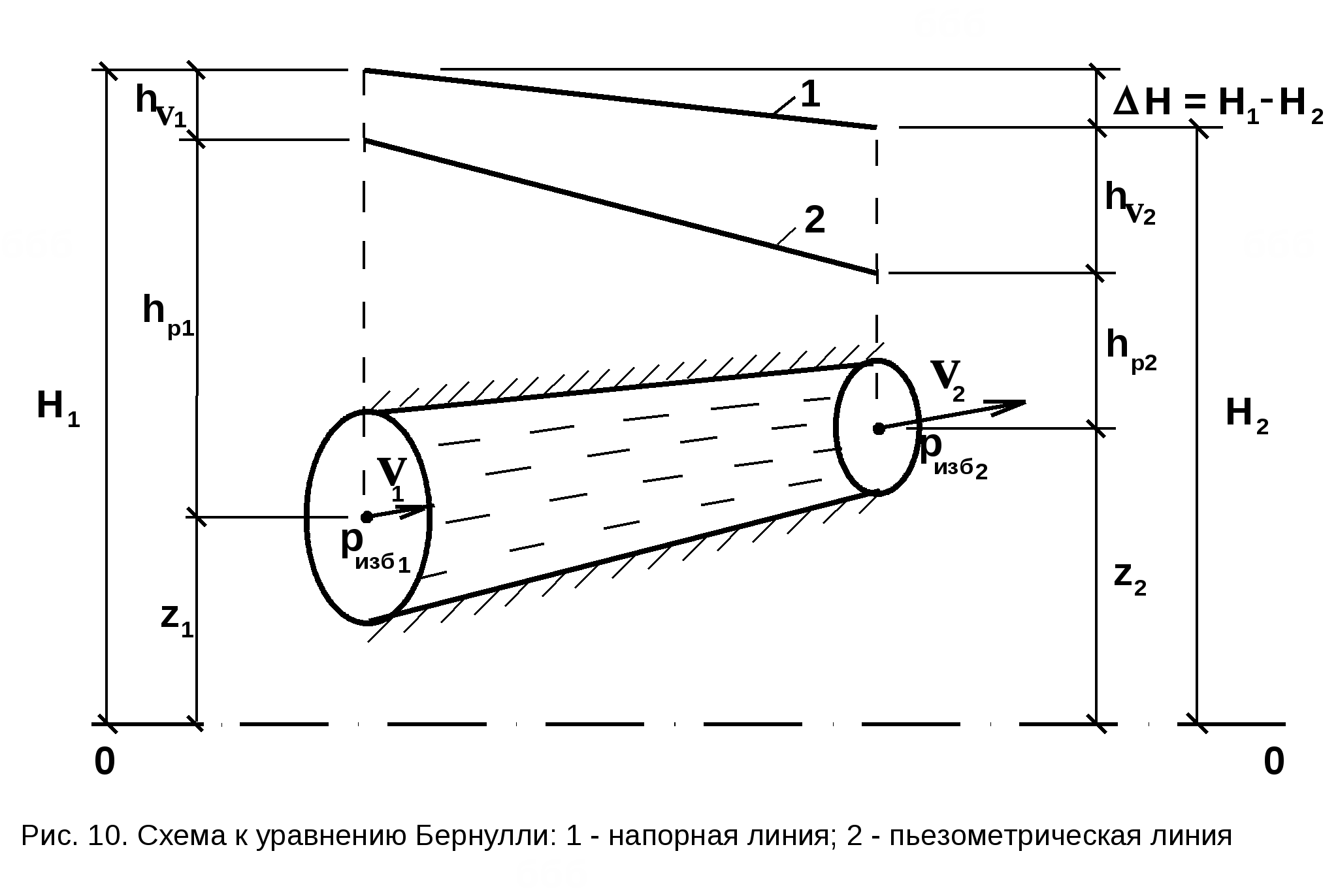

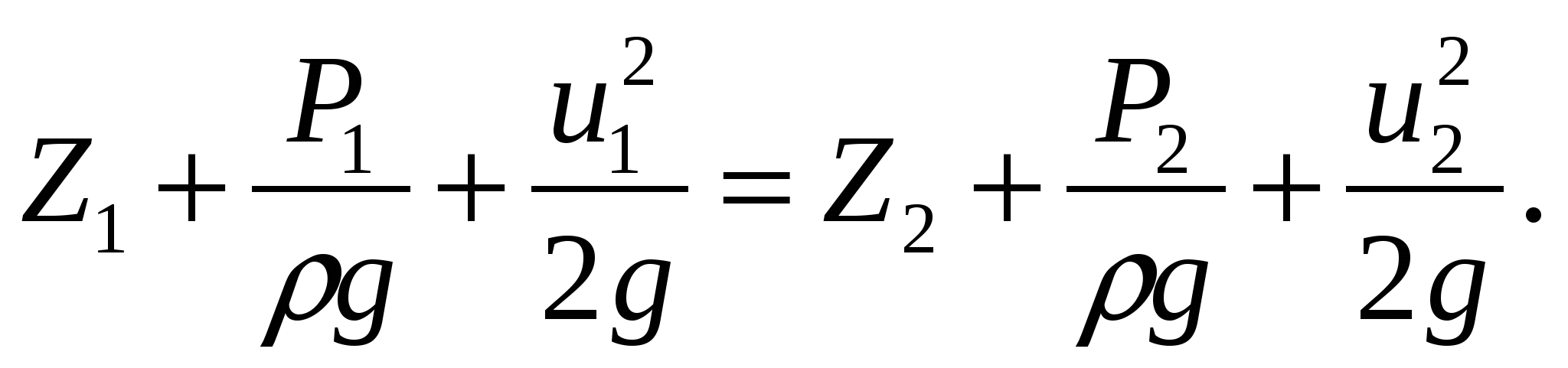
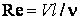 , где V – характерная скорость течения, l – характерный линейный размер,
, где V – характерная скорость течения, l – характерный линейный размер, 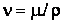 – кинематический коэффициент вязкости; Re – безразмерный параметр.
– кинематический коэффициент вязкости; Re – безразмерный параметр.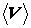 , полагая
, полагая 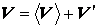 , где
, где 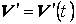 –так называемая флуктуация или пульсация скорости, которая считается малой добавкой к
–так называемая флуктуация или пульсация скорости, которая считается малой добавкой к 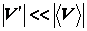 ; при этом фиктивное осредненное течение со скоростью
; при этом фиктивное осредненное течение со скоростью 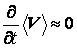 , а само турбулентное течение – квазистационарным. Аналогично осредняются и другие термогазодинамические параметры: p =
, а само турбулентное течение – квазистационарным. Аналогично осредняются и другие термогазодинамические параметры: p =  , T =
, T =  ,…
,…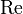 ), — безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье — Стокса[1]. Число Рейнольдса также считается критерием подобия течения вязкой жидкости.
), — безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье — Стокса[1]. Число Рейнольдса также считается критерием подобия течения вязкой жидкости.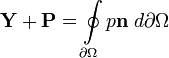

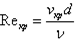

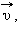 попадает в ящик и застревает в нем. По отклонению маятника можно определить скорость пули.
попадает в ящик и застревает в нем. По отклонению маятника можно определить скорость пули.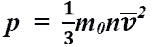 P=1\3*n*m*v^2
P=1\3*n*m*v^2