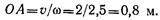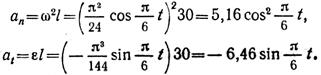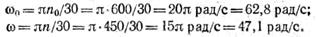Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1.9. Простейшие движения твердого телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Иметь представление о поступательном движении, его особенностях и параметрах, о вращательном движении тела и его параметрах. Знать формулы для определения параметров поступательного и вращательного движений тела. Уметь определять кинематические параметры тела при поступательном и вращательном движениях, определять параметры любой точки тела. Поступательное движение Поступательным называют такое движение твердого тела, при котором всякая прямая линия на теле при движении остается параллельной своему начальному положению (рис. 11.1, 11.2). При поступательном движении все точки тела движутся одинаково: скорости и ускорения в каждый момент одинаковы. Поэтому для описания движения тела можно рассматривать движение одной его точки, обычно центра масс.
Поступательное движение может быть прямолинейным и криволинейным.
Вращательное движение
При вращательном движении все точки тела описывают окружности вокруг общей неподвижной оси. Неподвижная ось, вокруг которой вращаются все точки тела, называется осью вращения. При этом каждая точка движется по окружности, радиус которой равен расстоянию точки до оси вращения. Точки на оси вращения не перемещаются.
φ — угол поворота тела, [ φ ] = рад; ω — угловая скорость, определяет изменение угла поворота в единицу времени, [ω] = рад/с.
Для определения положения тела в любой момент времени используется уравнение φ = f(t). Следовательно, для определения угловой скорости можно пользоваться выражением ω = dφ/dt. Иногда для оценки быстроты вращения используют угловую частоту вращения п, которая оценивается в оборотах в минуту. Угловая скорость и частота вращения физически близкие величины:
Изменение угловой скорости во времени определяется угловым ускорением ε, [ε] = рад/с2;
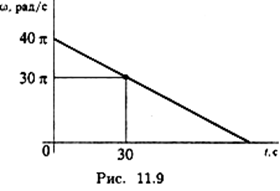
Частные случаи вращательного движения Равномерное вращение (угловая скорость постоянна): ω = const. Уравнение (закон) равномерного вращения в данном случае имеет вид: φ = φ0 + ωt. где φ0 – угол поворота до начала отсчёта.
Кинематические графики для этого вида движения изображены на рис. 11.4.
Равнопеременное вращение (угловое ускорение постоянно): ε = const. Уравнение (закон) равнопеременного вращения
гдеω0 — начальная угловая скорость.
Угловое ускорение при ускоренном движении — величина положительная, угловая скорость будет все время возрастать.
Угловое ускорение при замедленном движении — величина отрицательная; угловая скорость убывает. Для данного движения кинематические графики представлены на рис. 11.5.
Скорости и ускорения точек вращающегося тела
Тело вращается вокруг точки О. Определим параметры движения точки А, расположенной на расстоянии r а от оси вращения (рис. 11.6, 11.7).
Путь точки A: SA = ωrА Линейная скорость точки A: vA = ωrА Ускорения точки A: atA = ε rА — касательное; апA = ω2 rА — нормальное, где rА — радиус окружности, траектории точки А. Примеры решения задач
Пример 1. По заданному графику угловой скорости (рис.11.8)определить вид вращательного движения.
Решение 1. Участок 1 — неравномерное ускоренное движение, ω = φ/; е = ω/.
2. Участок 2 — скорость постоянна — движение равномерное, ω = const. 3. Участок 3 — скорость убывает равномерно — равнозамедленное движение, е = ω/ < 0.
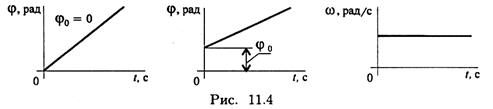
Пример 2. Ротор электродвигателя вращается со скоростью, описываемой уравнением ω = πt. Определить вид движения. Решение 1. Анализируем выражение для скорости: скорость меняется и зависит от времени линейно. Следовательно, угловое ускорение — постоянно, е = ω' = 2π = const. 2. Движение равнопеременное (равноускоренное, т.к. ускорение положительно). Пример 3. Тело вращалось равноускорено из состояния покоя и сделало 360 оборотов за 2 мин. Определить угловое ускорение. Решение 1. Один оборот равен 2π радиан. Следовательно: 360 оборотов = 720 π рад, φ = 720 π рад. 2.
Закон равнопеременного вращательного движения Пример 4. Тело вращалось с угловой частотой 1200 об/мин. Затем движение стало равнозамедленным, и за 30 секунд скорость упала до 900 об/мин. Определить число оборотов тела за это время и время до полной остановки. Использовать пункт 1 примера 3.
Решение 1. Построить график изменения скорости за 30 с (рис. 11.9).
Определяем угловую скорость вращения тела:
Определяем угловое ускорение:
Определяем угол поворота за прошедшее время:
Число оборотов за 30 с:
2. Определяем время до полной остановки. Скорость при остановке равна нулю, ω = 0. Таким образом, ω = ω0 + et 0 = ω0 + et Тогда t0CT = -ω0/ε tocr = 40π*3/π = 120 c. Пример 5. Маховое колесо вращается равномерно со скоростью 120 об/мин (рис. 11.10). Радиус колеса 0,3 м. Определить скорость и полное ускорение точек на ободе колеса, а также скорость точки, находящейся на расстоянии 0,15 м от центра.
Решение
Касательное ускорение точки A a tA = 0; нормальное ускорение точки А аnA = ω2rA апA = (12,56)2 • 0,3 = 47,3м/с2. 5. Полное ускорение точек на ободе колеса
Пример 6. Точка начала двигаться равноускорено по прямой из состояния покоя и через 25 с ее скорость стала равна 50 м/с. С этого момента точка начала равнозамедленное движение по дуге окружности радиуса г = 200 м и через 20 с ее скорость снизилась до 10 м/с. После этого точка продолжила свое движение с этой скоростью по прямой и через 5 с внезапно остановилась. Определить: 1) среднюю скорость точки на всем пути; 2) полное ускорение точки через 10 с после начала ее равнозамедленного движения по окружности. Решение
1. 2. Рассмотрим движения точки по отрезку АВ:
3. Рассмотрим движение точки по дуге ВС:
4. Рассмотрим движение точки на отрезке CD:
5. Определим среднюю скорость точки на всем пути по траектории движения ABCD (см. рис. 5):
tABCD = tAB + tBC + tCD = 25 + 20 + 5 = 50 c
6. Определим значение полного ускорения точки через 5 с после начала равнозамедленного движения (см. положение К на рис. 5)
Полное ускорение
Пример 7. Тело начало вращаться из состояния покоя и через 15 с его угловая скорость достигла 30 рад/с. С этой угловой скоростью тело вращалось 10 с равномерно, а затем стало вращаться равнозамедленно в течение 5 с до полной остановки. Определить: 1) число оборотов и среднюю угловую скорость тела за все время вращения; 2) окружную скорость точек тела, расположенных на расстоянии r = 0,5 м от оси вращения тела через 5 с после начала движения. Решение
1. Разграничим вращательное движение данного тела на участки равноускоренного, равномерного и равнозамедленного движения. Определим параметры вращательного движения тела по этим участкам. 2. Равноускоренное вращение (участок 1):
3. Равномерное вращение (участок II):
4. Равнозамедленное вращение (участок III):
5. Определим полное число оборотов тела за все время вращения:
6. Определим среднюю угловую скорость тела за все время вращения:
7. Определим окружную скорость точек тела, расположенных на расстоянии r = 0,5 м от оси вращения через 5 с после начала движения тела:
Пример 8. Диск радиусом R = 2 м вращается вокруг неподвижной оси согласно уравнению
(φ — в радианах, t — в секундах). Определить скорость и ускорение точки поверхности диска в моменты времени t1 = 0 и t2 = 2 с. Решение
Для определения скорости и ускорения точки необходимо знать угловую скорость и угловое ускорение диска. Уравнение изменения угловой скорости диска:
Уравнение изменения углового ускорения диска:
Определим угловую скорость и угловое ускорение диска в моменты времени t1 = 0 и t2 = 2 с:
Определим скорость точки поверхности диска в указанные моменты времени:
Определим нормальное и касательное ускорения точки поверхности диска в моменты времени t1 и t2:
Тогда
Решение
Здесь для решения следует воспользоваться известными соотношениями для линейной скорости и нормального ускорения точек вращающегося тела:
Если второе уравнение разделить на первое, найдем угловую скорость вращения шкива:
Тогда
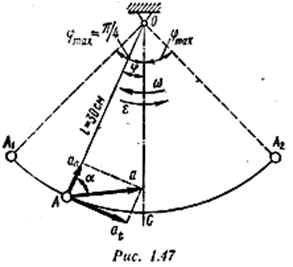
Пример 10. Шарик А (рис. 1.47), подвешенный на стержне OA, колеблется в вертикальной плоскости около неподвижной горизонтальной оси О согласно уравнению
(φ — в радианах, t — в секундах). Определить: 1. Ближайшие моменты времени, соответствующие максимальным отклонениям стержня OA от вертикали OC вправо и влево, а также значение максимальных углов отклонения. 2. Ближайший момент времени после начала движения, при котором нормальное ускорение шарика равно нулю. 3. Ближайший момент времени, при котором касательное ускорение шарика равно нулю. 4. Полное ускорение шарика при t = 1,5 с и угол, образованный вектором ускорения со стержнем OA. Решение
Стержень OA совершает вращательное (колебательное) движение. Максимальные углы отклонения стержня от вертикали соответствуют наибольшим абсолютным значениям функции sin (πt/6). Очевидно, это имеет место при sin (πt/6) = ± 1:
При t1 = 3 с φтах = π /4, при t2 = 9 с φтах = -- π/4. Крайние положения стержня OA на рис. 1.47 показаны штриховыми линиями OA1 и ОА2. Напомним, что за положительное направление считаем вращение по часовой стрелке. Уравнение изменения угловой скорости стержня OA
Уравнение изменения углового ускорения стержня OA
Направления ω и ε показаны на рис. 1.47. В приведенном примере направления ω и ε противоположны. Следовательно, стержень OA совершает замедленное вращательное движение. Нормальное и касательное ускорения шарика определяются по формулам:
В рассматриваемом примере касательное ускорение шарика направлено к точке С (рис. 1.47). Определим момент времени, при котором ап равно нулю. Для этого выражение ап приравняем нулю:
Записанное условие выполняется при
но
Тогда
Нормальное ускорение шарика равно нулю, когда стержень OA занимает крайние положения. Определим момент времени, при котором at равно нулю. Для этого выражение at приравняем нулю:
Это условие выполняется при
Касательное ускорение шарика обращается в ноль в тот момент, когда стержень OA совпадает с линией OC. Вычислим аn и at при t = 1,5 с:
Ускорение шарика при t = 1,5 с
Угол между вектором ускорения шарика и стержнем OA определяется из соотношения
Откуда
Пример 11. Через 30 с равномерного вращательного движения с частотой n 0 = 600 об/мин тело начало равнозамедленное движение и в течение последующих 20 с частота вращения тела уменьшилась до n = 450 об/мин. Определить угловое ускорение тела при равнозамедленном вращательном движении, а также количество оборотов тела за время равномерного и равнозамедленного движения. Решение
1. Переведем начальную и конечную частоты вращения тела в единицы угловой скорости:
2. За время t1 = 30 с тело, вращаясь равномерно с угловой скоростью ω0 = 20π рад/с, повернулось на угол
3. По формуле угловое ускорение, с которым тело вращалось в течение времени t2 = 20 с
4. За время равнозамедленного движения тело повернулось на угол
5. За весь промежуток времени t1 + t2 = 50 с тело повернулось на угол
следовательно, тело сделало
Для определения количества оборотов, сделанных телом, можно было частоту вращения и не переводить в единицы угловой скорости. За время t1 = 30 с = 0,5 мин при равномерном движении тело сделало
За время t2 = 20 с = 1/3 мин при равнозамедленном вращении тело сделало
Всего
Контрольные вопросы и задания
1. Какими кинематическими параметрами характеризуется поступательное движение и почему? 2. Запишите уравнение равномерного поступательного движения твердого тела. 3. Запишите уравнение равнопеременного поступательного движения твердого тела. 4. Запишите уравнения равномерного и равнопеременного вращательного движений твердого тела. 5. Задано уравнение движения тела S = f(t). Как определяют скорость и ускорение? 6. Для заданного закона (уравнения) движения φ = 6,28 + 12 t + 3 t 2 выберите соответствующий кинематический график движения (рис. 11.11).
7. Для движения, закон которого задан в вопросе 6, определите угловое ускорение в момент t = 5 с.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 6071; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.014 с.) |


 Для описания вращательного движения тела вокруг неподвижной оси можно использовать только угловые параметры (рис. 11.3):
Для описания вращательного движения тела вокруг неподвижной оси можно использовать только угловые параметры (рис. 11.3):







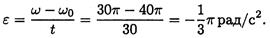




 Представим траекторию движения точки, как показано на рис. 5. Весь путь, пройденный точкой, разбиваем на участки равноускоренного (по отрезку АВ), равнозамедленного (по дуге ВС) и равномерного (по отрезку CD) движения.
Представим траекторию движения точки, как показано на рис. 5. Весь путь, пройденный точкой, разбиваем на участки равноускоренного (по отрезку АВ), равнозамедленного (по дуге ВС) и равномерного (по отрезку CD) движения.
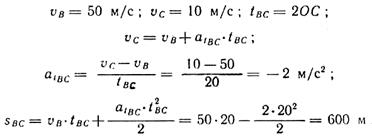




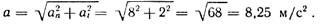





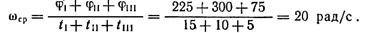



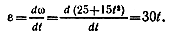




 Пример 9. Точка А, лежащая на ободе равномерно вращающегося шкива, движется со скоростью v = 2 м/с и нормальным ускорением ап = 5 м/с2. Определить радиус шкива OA и величину угловой скорости (рис. 1.46).
Пример 9. Точка А, лежащая на ободе равномерно вращающегося шкива, движется со скоростью v = 2 м/с и нормальным ускорением ап = 5 м/с2. Определить радиус шкива OA и величину угловой скорости (рис. 1.46).